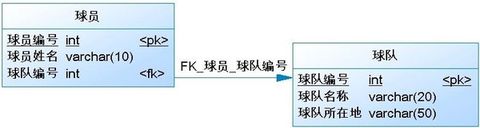
关联映射:一对多/多对一
存在最普遍的映射关系,简单来讲就如球员与球队的关系;
一对多:从球队角度来说一个球队拥有多个球员 即为一对多
多对一:从球员角度来说多个球员属于一个球队 即为多对一
数据表间一对多关系如下图:
关联映射:一对一
一对一关系就如球队与球队所在地址之间的关系,一支球队仅有一个地址,而一个地址区也仅有一支球队。
数据表间一对一关系的表现有两种,一种是外键关联,一种是主键关联。图示如下:
一对一外键关联:

一对一主键关联:要求两个表的主键必须完全一致,通过两个表的主键建立关联关系

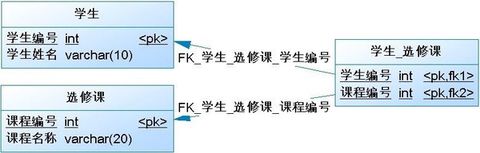
关联映射:多对多
多对多关系也很常见,例如学生与选修课之间的关系,一个学生可以选择多门选修课,而每个选修课又可以被多名学生选择。
数据库中的多对多关联关系一般需采用中间表的方式处理,将多对多转化为两个一对多。
数据表间多对多关系如下图:
每天学一点,每天积累一天,进步就不止一点点!PS:好记性不如烂笔头,学会总结,学会思考~~~ ----要飞翔,必须靠自己!
















代码)


