文章目录
- 1 插入排序
- 2 希尔(shell)排序
- 3 冒泡排序
- 4 快速排序
- 5 选择排序
- 6 堆排序
- 7 归并排序
- 8 内排序代码一览
- 运行结果
- 常用排序算法时间复杂度和空间复杂度一览表
- 排序:将一组杂乱无章的数据按一定的规律顺次排列起来,可以看作是线性表的一种操作。
- 内排序:排序期间元素全部存放在内存中的排序。
- 并非所有内部排序算法都基于比较操作,基数排序就不基于比较。
- 排序算法的好坏如何衡量?
- 时间效率——排序速度(即排序所花费的全部比较次数)
- 空间效率——占内存辅助空间的大小
- 稳定性——若两个记录A和B的关键字值相等,但排序后A、B的先后次序保持不变,则称这种排序算法是稳定的。
- 算法是否具有稳定性并不能衡量一个算法的优劣,它主要是对算法性质进行描述,内部排序算法的性能取决于算法的时间复杂度和空间复杂度,时间复杂度一般是由比较和移动次数决定。
- “快速排序”是否真的比任何排序算法都快?
基本上是,因为每趟可以确定的数据元素是呈指数增加的。
1 插入排序
插入排序的基本思想是:
每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。
简言之,边插入边排序,保证子序列中随时都是排好序的。
在已形成的有序表中线性查找,并在适当位置插入,把原来位置上的元素向后顺移。

时间效率:
因为在最坏情况下,所有元素的比较次数总和为(0+1+…+n-1)→O(n2)。
其他情况下也要考虑移动元素的次数。 故时间复杂度为O(n2)
空间效率:
仅占用1个缓冲单元——O(1)
算法的稳定性:
因为25*排序后仍然在25的后面——稳定
直接插入排序算法的实现:
void InsertSort ( int arr[],int n ) { int i,j,temp; //temp暂存待插关键字for ( i = 1; i <=n; i++) //依次将A[2]~A[n]插入到前面已排序的序列{ temp=arr[i]; j=i-1 ; //从i-1往前扫描while(j>=0 && temp<arr[j]){ arr[j+1]= arr[j]; //向后挪位--j ; } arr[j+1]= temp; //复制到插入元素 }
}
直接插入排序适用于顺序存储和链式存储的线性表
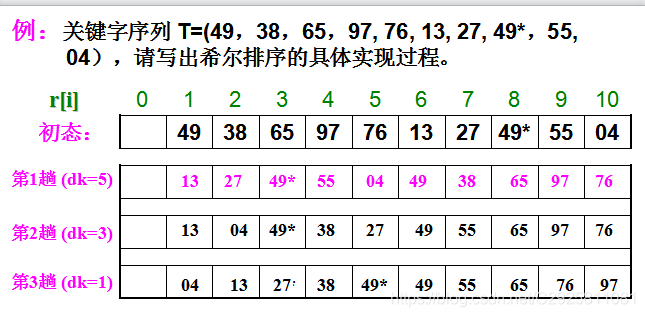
2 希尔(shell)排序
基本思想:
先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
优点:
让关键字值小的元素能很快前移,且序列若基本有序时,再用直接插入排序处理,时间效率会高很多。
void ShellSort(ElementType A[], int N) { /* 希尔增量序列 */for (D = N / 2; D > 0; D /= 2) { //D=1即直接插入排序/* 插入排序 */for (i = D; i < N; i++) {tmp = A[i];for(j = i; j >= D && A[j - D] > tmp; i -= D) {A[j] = A[j - D];}A[i] = tmp;}}
}
时间复杂度
1.原始数据如下共有16个数据:
1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 15 | 8 | 16 |
2.进行 8 间隔排序后(未发生变化):
1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 15 | 8 | 16 |
3.进行 4 间隔排序后(未发生变化):
1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 15 | 8 | 16 |
4.进行 2 间隔排序后(未发生变化):
1 | 9 | 2 | 10 | 3 | 11 | 4 | 12 | 5 | 13 | 6 | 14 | 7 | 15 | 8 | 16 |
5.进行 1 间隔排序后(1间隔排序也就是插入排序):
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
最坏情况(与插入排序一样)
T=O(n2)T = O(n^2)T=O(n2)
结论:
那么来观察它的间隔数 8 4 2 1,发现其间隔增量元素并不互质,则小的增量根本不起作用
稳定性:
由于不是相邻元素的比较和交换,它是不稳定的
希尔排序仅适用于线性表为顺序存储的情况
3 冒泡排序
基本思路:
每趟不断将记录两两比较,并按“前小后大”(或“前大后小”)规则交换。
优点:
每趟结束时,不仅能挤出一个最大值到最后面位置,还能同时部分理顺其他元素;一旦下趟没有交换发生,还可以提前结束排序。
前提:顺序存储结构

void BubleSort(int arr[]),int n)
{int i,j,flag;int temp;for(i=n-1;i>=1;--i){flag=0; //表示本趟冒泡是否发生交换的标志for(int j=1;j<=i;j++)if(arr[j-1]>arr[j]){temp=arr[j];arr[j]=arr[j-1];arr[j-1]=temp;flag=1; //发生交换则置flag为1}if(flag==0) //未发生交换,结束return;}
}
冒泡排序的算法分析:
- 时间效率:O(n2) —因为要考虑最坏情况
- 空间效率:O(1) —只在交换时用到一个缓冲单元
- 稳 定 性: 稳定 —25和25*在排序前后的次序未改变
- 冒泡排序的优点:每一趟整理元素时,不仅可以完全确定一个元素的位置(挤出一个泡到表尾),还可以对前面的元素作一些整理,所以比一般的排序要快。
4 快速排序
基本思想:
从待排序列中任取一个元素 (例如取第一个) 作为中心,所有比它小的元素一律前放,所有比它大的元素一律后放,形成左右两个子表;然后再对各子表重新选择中心元素并依此规则调整,直到每个子表的元素只剩一个。此时便为有序序列了。
优点:
因为每趟可以确定不止一个元素的位置,而且呈指数增加,所以特别快!
前提:
顺序存储结构

void QuickSort(int A[],int low,int high)
{if(low<high){ //明确的递归终止条件 int pivotpos=Partition(A,low,high); //划分 QuickSort(A,low,pivotpos-1);QuickSort(A,pivotpos+1,high);}
}int Partition(int A[],int low,int high) //将待排序的数组划分两个子表的操作
{int pivot=A[low]; //将当前表中的第一个元素设为比较值,对表进行划分 while(low<high){ //递归跳出的条件 while(low<high&&A[high]>=pivot) --high;A[low]=A[high]; //将比比较值小的元素移动到左端 while(low<high&&A[low]<=pivot)++low;A[high]=A[low]; //将比比较值大的元素移动到右端}A[low]=pivot; //比较元素存放在最终位置 return low; //返回存放比较值的最终位置
}
快排算法分析:
- 时间效率:O(nlog2n) —因为每趟确定的元素呈指数增加
- 空间效率:O(log2n)—因为递归要用栈(存每层low,high和pivot)
- 稳 定 性: 不 稳 定 —因为有跳跃式交换。
5 选择排序
选择排序的基本思想:
每经过一趟比较就找出一个最小值,与待排序列最前面的位置互换即可。
——首先,在n个记录中选择最小者放到r[1]位置;然后,从剩余的n-1个记录中选择最小者放到r[2]位置;…如此进行下去,直到全部有序为止。

优点:实现简单
缺点:每趟只能确定一个元素,表长为n时需要n-1趟
前提:顺序存储结构
void SelectionSort(ElementType A[], int N)
{for (i = 0; i < N; i++) {/* 从 A[i] 到 A[N - 1] 中找最小元素,并将其位置赋值给 MinPosition */MinPosition = ScanForMin(A, i, N - 1);/* 将未排序部分的最小元素换到有序部分的最后位置 */Swap(A[i], A[MinPosition]);}
}
6 堆排序
- 堆的定义:设有n个元素的序列 k1,k2,…,kn,当且仅当满足下述关系之一时,称之为堆。
解释:如果让满足以上条件的元素序列 (k1,k2,…,kn)顺次排成一棵完全二叉树,则此树的特点是:树中所有结点的值均大于(或小于)其左右孩子,此树的根结点(即堆顶)必最大(或最小)。
- 怎样建堆?
步骤:从最后一个非终端结点开始往前逐步调整,让每个双亲大于(或小于)子女,直到根结点为止。
堆排序算法分析:
- 时间效率: O(nlog2n)。因为整个排序过程中需要调用n-1次HeapAdjust( )算法,而算法本身耗时为log2n;
- 空间效率:O(1)。仅在第二个for循环中交换记录时用到一个临时变量temp。
稳定性: 不稳定。- 优点:对小文件效果不明显,但对大文件有效。
7 归并排序
归并排序算法的基本思想 :
(1) 初始无序序列看成n个有序子序列,每个子序列长度为1;
(2) 两两合并,得到└n/2┘个长度为2或1的有序子序列;
(3) 重复步骤2直至得到一个长度为n的有序序列为止。
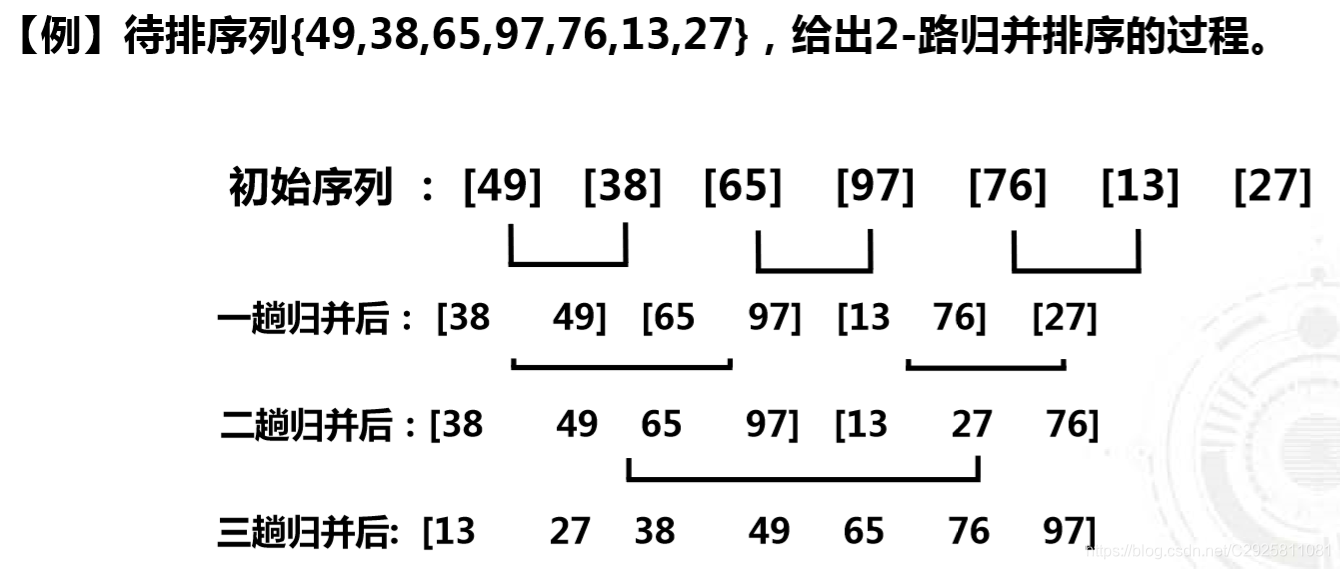
两个有序表合并成一个有序表
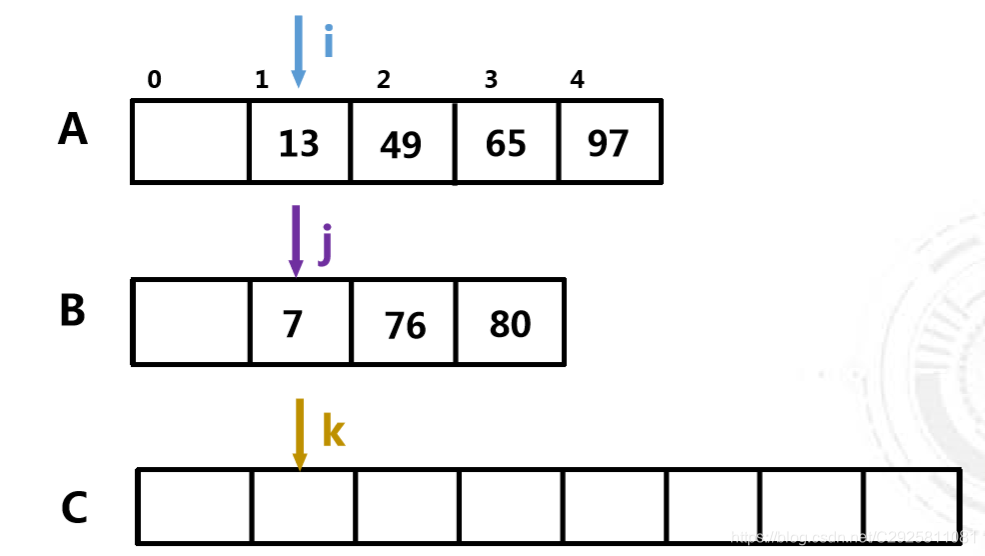
合并算法:
//将有序表A[low..mid]和A[mid+1,high] 归并为有序表B[low..high] void Merge(ElementType A[], ElementType B[], int low, int mid, int high){ i = low; j=mid+1; k=low; while (i <=mid && j <=high) { if (A[i] < A[j]) B[k++] = A[i++]; else B[k++] = A[j++]; } while (i <=mid) B[k++] = A[i++]; while (j <= high) B[k++] = A[j++]; }
给定区间的归并算法 :
//将A[low…high]中的序列归并排序后放到B[low…high]中
void MSort(ElementType A[], ElementType B[], int low, int high){ if (low==high) B[low]=A[low]; else { mid=(low+high)/2; //将当前序列一分为二,求出分裂点mid Msort(A, S, low, mid); //对子序列A[low..mid]递归归并排序结果放入S[low..mid] Msort(A, S, mid+1,high); //对子序列A[mid+1..high]递归归并排序,结果放入S[mid+1..high] Merge(S, B, low, mid, high); //将S[low..mid]和S[mid+1..high]归并到B[low..high] } }
归并排序算法实现:
void MergeSort(ElementType A[]) { //对顺序表A做归并排序 Msort(A, C, 1, A.length); }
归并排序算法分析:
- 时间效率:O(nlog2n)
- 空间效率:O(n)
- 稳 定 性:稳定
8 内排序代码一览
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<time.h>
#include<Windows.h>
typedef int keytype;
typedef struct {keytype key;/*关键字码*/
}RecType;int s[50][2];/*辅助栈s*/
void PrintArray(RecType R[],int n)
{int i;for(i=0;i<n;i++)printf("%6d",R[i].key);printf("\n");
}
void InsertSort(RecType R[],int n)/*用直接插入排序法对R[n]进行排序*/
{int i,j;RecType temp;for(i=0;i<=n-2;i++){temp=R[i+1];j=i;while (temp.key<=R[j].key && j>-1){R[j+1]=R[j];j--;}R[j+1]=temp;}
}
void ShellInsert(RecType *r,int dk,int n)
{int i,j;keytype temp;for(i=dk; i<n; ++i )if(r[i].key <r[i-dk].key ) //将r[i]插入有序子表{temp=r[i].key;r[i].key=r[i-dk].key;for(j=i-2*dk;j>-1 && temp<r[j].key; j-=dk )r[j+dk].key=r[j].key; // 记录后移r[j+dk].key = temp; // 插入到正确位置}
}
void ShellSort(RecType *L,int dlta[],int t,int n)/*希尔排序*/
{
// 按增量序列 dlta[t-1] 对顺序表L作希尔排序int k;for(k=0;k<t;k++)ShellInsert(L,dlta[k],n); //一趟增量为 dlta[k] 的插入排序
} // ShellSort
void CreatArray(RecType R[],int n)
{int i;Sleep(1000);srand( (unsigned)time( NULL ) );for(i=0;i<n;i++)R[i].key=rand()%1000;
}
void BubbleSort(RecType R[],int n) /*冒泡排序*/
{int i,j,flag;keytype temp;for(i=0;i<n-1;i++){flag=0;for(j=0;j<n-i-1;j++){if(R[j].key>R[j+1].key){temp=R[j].key;R[j].key=R[j+1].key;R[j+1].key=temp;flag=1;}}if(flag==0)break;}
}
int Hoare(RecType r[],int l,int h)/*快速排序分区处理*/
{int i,j;RecType x;i=l;j=h;x=r[i];do{while(i<j && r[j].key>=x.key)j--;if(i<j){r[i]=r[j];i++;}while(i<j && r[i].key<=x.key)i++;if (i<j){r[j]=r[i];j--;}}while(i<j);r[i]=x;return(i);
} /*Hoare*/
void QuickSort1(RecType r[],int n) /*快速排序非递归*/
{int l=0,h=n-1,tag=1,top=0,i;do{while (l<h){i=Hoare(r,l,h);top++;s[top][0]=i+1;s[top][1]=h;h=i-1;}/*tag=0表示栈空*/if (top==0)tag=0;else{l=s[top][0];h=s[top][1];top--;}}while (tag==1); /*栈不空继续循环*/
} /*QuickSort1*/
void SelectSort(RecType R[],int n)/*直接选择排序*/
{int i,j,k; RecType temp;for(i=0;i<n-1;i++){k=i;/*设第i个记录关键字最小*/for(j=i+1;j<n;j++)/*查找关键字最小的记录*/if(R[j].key<R[k].key)k=j;/*记住最小记录的位置*/if (k!=i) /*当最小记录的位置不为i时进行交换*/{temp=R[k];R[k]=R[i];R[i]=temp;}}
}
void HeapAdjust(RecType R[],int l,int m)/*堆排序筛选*/
{/*l表示开始筛选的结点,m表示待排序的记录个数。*/int i,j;RecType temp;i=l;j=2*i+1; /*计算R[i]的左孩子位置*/temp=R[i]; /*将R[i]保存在临时单元中*/while(j<=m-1){if(j<m-1 && R[j].key<R[j+1].key)j++; /*选择左右孩子中最大者,即右孩子*/if(temp.key<R[j].key)/*当前结点小于左右孩子的最小者*/{R[i]=R[j];i=j;j=2*i+1;}else /*当前结点不小于左右孩子*/break;}R[i]=temp;
}
void HeapSort(RecType R[],int n)/*堆排序*/
{int j;RecType temp;for(j=n/2-1;j>=0;j--) /*构建初始堆*/HeapAdjust(R,j,n);/*调用筛选算法*/for(j=n;j>1;j--) /*将堆顶记录与堆中最后一个记录交换*/{temp=R[0];R[0]=R[j-1];R[j-1]=temp;HeapAdjust(R,0,j-1);/*将R[0..j-1]调整为堆*/}
}
void Merge(RecType aa[],RecType bb[],int l,int m,int n)
{/*将两个有序子序列aa[1…m]和aa[m+1,…n]合并为一个有序序列bb[1…n]*/int i,j,k;k=l;i=l;j=m+1;/*将i,j,k分别指向aa[1…m]、aa[m+1,…n]、bb[1…n]首记录*/while (i<=m && j<=n) /*将aa中记录由小到大放入bb中*/if(aa[i].key<=aa[j].key)bb[k++]=aa[i++];elsebb[k++]=aa[j++];while (j<=n) /*将剩余的aa[j…n]复制到bb中*/bb[k++]=aa[j++];while (i<=m) /*将剩余的aa[i…m]复制到bb中*/bb[k++]=aa[i++];
}
void MergeOne(RecType aa[],RecType bb[],int len,int n)
{/*从aa[1…n]]归并到bb[1…n],其中len是本趟归并中有序表的长度*/int i;for(i=0;i+2*len-1<=n;i=i+2*len)Merge(aa,bb,i,i+len-1,i+2*len-1);/*对两个长度为len的有序表合并*/if(i+len-1<n) /*当剩下的元素个数大于一个子序列长度len时*/Merge(aa,bb,i,i+len-1,n);else /*当剩下的元素个数小于或等于一个子序列长度len时*/Merge(aa,bb,i,n,n); /*复制剩下的元素到bb中*/
}
void MergeSort(RecType aa[],RecType bb[],int n)//归并排序
{int len=1; /*len是排序序列表的长度 */while (len<n){MergeOne(aa,bb,len,n-1);MergeOne(bb,aa,2*len,n-1);len=4*len;}
}int main()
{int n,data[3]={4,2,1},cord;RecType *r,*bb;printf("Please input number:");scanf("%d",&n);r=(RecType *)malloc(sizeof(RecType)*n);bb=(RecType *)malloc(sizeof(RecType)*n);memset(bb,0,sizeof(RecType)*n);do{printf("\n 主菜单 \n");printf("1----插入排序\n");printf("2----希尔排序\n");printf("3----冒泡排序\n");printf("4----快速排序\n");printf("5----选择排序\n");printf("6----堆排序\n");printf("7----归并排序\n");printf("8----退出\n");scanf("%d",&cord);switch(cord){case 1:memset(r,0,sizeof(RecType)*n);CreatArray(r,n);PrintArray(r,n);InsertSort(r,n);PrintArray(r,n);break;case 2:memset(r,0,sizeof(RecType)*n);CreatArray(r,n);PrintArray(r,n);ShellSort(r,data,3,n);PrintArray(r,n);break;case 3:memset(r,0,sizeof(RecType)*n);CreatArray(r,n);PrintArray(r,n);BubbleSort(r,n);PrintArray(r,n);break;case 4:memset(r,0,sizeof(RecType)*n);CreatArray(r,n);PrintArray(r,n);QuickSort1(r,n);PrintArray(r,n);break;case 5:memset(r,0,sizeof(RecType)*n);CreatArray(r,n);PrintArray(r,n);SelectSort(r,n);PrintArray(r,n);break;case 6:memset(r,0,sizeof(RecType)*n);CreatArray(r,n);PrintArray(r,n);HeapSort(r,n);PrintArray(r,n);break;case 7:memset(r,0,sizeof(RecType)*n);CreatArray(r,n);PrintArray(r,n);MergeSort(r,bb,n);PrintArray(r,n);break;case 8:exit(0);default:cord=0;}}while(cord<=8);return 0;
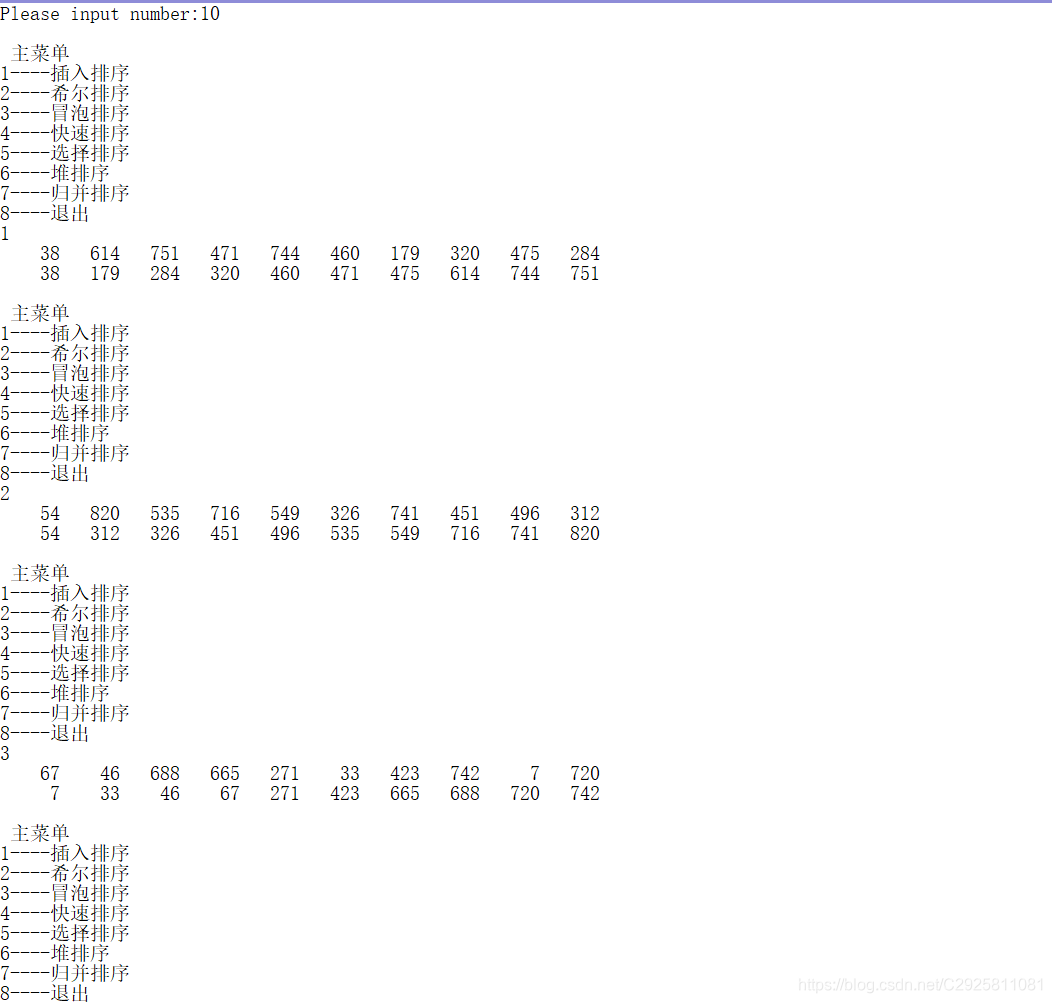
}运行结果
常用排序算法时间复杂度和空间复杂度一览表
| 排序法 | 最差时间分析 | 平均时间复杂度 | 稳定度 | 空间复杂度 |
|---|---|---|---|---|
| 冒泡排序 | O(n^2) | O(n^2) | 稳定 | O(1) |
| 快速排序 | O(n^2) | O(n*log2n) | 不稳定 | O(log2n)~O(n) |
| 选择排序 | O(n^2) | O(n^2) | 稳定 | O(1) |
| 2-路归并排序 | O(n*log2n) | O(n*log2n) | 是 | O(n) |
| 插入排序 | O(n^2) | O(n^2) | 稳定 | O(1) |
| 堆排序 | O(n*log2n) | O(n*log2n) | 不稳定 | O(1) |
| 希尔排序 | O | O | 不稳定 | O(1) |








)










