1.搜索问题

• 搜索问题——对原问题的建模
  • 构成：
    • 状态空间
      • 包含环境中每一个细节
      • 搜索状态：只保留行动需要的细节
    • 后继函数
      • 行动，消耗
    • 初始状态和目标测试
  • 解：
    • 一个行动序列，将初始状态–>目标状态
  • 表示
    • 状态空间图
      • 搜索问题的数学表示
      • 每种状态只出现一次
      • 不在内存中构建（大），但很有用
    • 搜索树
      • 根节点：初始状态
      • 子节点：父节点的后继状态
      • 节点：状态，对应到达这个状态的行动
      • 对大多问题，不会构建整棵树
    • 树中节点对应于图中节点的某条完整路径
    • 大量重复结构：在树中–>无穷大
  • 搜索
    • 扩展出潜在行动
    • 维护所考虑行动的* * 边缘* * （还未处理的节点，叶子）
    • 试图扩展尽可能少的树节点
  • 主要：
    • 边缘
    • 扩展
    • 探索策略–对应于各个搜索算法

2.全局搜索—保留了所有的路径

• 参数说明
  • b-分支因子
  • m-最大深度
  • d-最浅层的目标节点的深度
  • l-限制下的深度，
  • $C^* /\epsilon $:UCS取得最优解时估计深度，$\epsilon$是最小cost，$C^* $是解的cost，
  • 整棵树的深度：
  • $1+b^1+...+b^m=O(b^m)$

算法名称	算法策略	时间复杂度	空间复杂度	完备性	最优性	存储
DFS(深度优先）	深度优先（从左往右，得到最左结果，	$O(b^m)$	$O(bm)$	（不完备）有限就有解	无	堆栈
Depth-limited(深度优先）	深度优先,限制最长搜索深度，超过就换一条	$O(b^l)$	$O(bl)$	（不完备）m有限就有解	无	堆栈
Iterative-Depth(深度优先）	逐层限制深度，使用DFS（DFS的空间+BFS的最优)	$O(b^d)$	$O(bd)$	有解，s必然有限	无	堆栈
BFS	宽度优先，会得到最浅层的解	$O(b^d)$	$O(b^d)$	有解，s必然有限（完备)	最优（无权时才最优	队列
UCS(代价一致搜索	优先队列BFS，考虑当前代价（优先级）,BFS是UCS的特例，g(x)	$O(b^{[}{C}^{\ast }/ϵ])$	$O(b^{[}{C}^{\ast }/ϵ])$	完备	最优	优先队列
启发式搜索	使用额外信息（如到终点的长度）–启发函数h(x)	-	-	-	-	-
贪婪搜索	h(x)最好的先扩展	快速，最坏同DFS(全树扩展）	-	有限图时完备	最大问题在于往往找不到最优解	优先队列
A*	UCS+贪婪,优先级用f(x)=g(x)+h(x),目标出列时才停止	指数	指数	有限图时完备	实际h>估计h，且目标出列时结束的情况，最优（往好了估计）	花费的话小的优先队列
A* 图搜索	去除树中重复节点(一个状态则不扩展）（保证h(A)<=实际，且h(A)-h©<=弧cost(一致性）	指数	指数	完备(树有的状态他都有）	弧一致时最优	优先队列

BFS/DFS

https://blog.csdn.net/qq_40763929/article/details/81675163

• 什么情况下DFS比BFS好？
  • 解决连通性问题，用DFS
  • 解决最短路径问题，用BFS
• 迭代深入搜索存在浪费冗余吗？
  • 通常绝大多数的节点在底层，所以上层的节点生成多次影响不大

2.2 启发式搜索

• 结束条件
  • 目标出列时才结束
  • 如果目标入列时结束？得不到最优解
• g(x)前向代价，已经花费的
• h(x)后向代价，预计还要花费的 —启发函数
• f(x)
• A* 最优？
  • 需要实际消耗>估计消耗–往好了估计
  • 若实际消耗<估计消耗：得不到最优解（启发函数设计的不合理）
  • 保证往好了估计—可采纳启发
    • 可采纳启发：0<=h(x)<=h* (x)(实际
    • 获得：
      • 原问题的松弛问题的解（简化原问题）
        • 原，空格移动问题
        • eg：棋子可以从A–>B
        • eg:相邻，则可移动（不论隔壁有无东西）
      • 实际耗散（难算）
      • 好坏：
        • 占优势：ha>=hc if 任意n，ha(n)>=hc(n)
          • a扩展的节点包含于c
        • 若无包含性，则取最大：
          • h(n)=max(ha(n),hb(n))
    • 特点
      • 越接近原问题，需要扩展的节点越少
      • 越接近原问题，计算越多
  • 证明最优（使用了可采纳启发）
    • B-次优，A-最优，h-可采纳的，证明A在B前离开边缘集合（出队列)
      • 假设B和A的祖先n在边缘集合上
      • 那么，n会在B之前被扩展
        1. f(n)<=f(A)(因为还未到达终点，f(A)=g(A)就是实际全程耗散）
        2. f(A)<f(B)(g(A)<g(B),且h(A)=h(B)=0到达终点了）
        3. 所以，n先扩展
      • 所以A的所有祖先都在B之前扩展
      • A在B之前扩展
      • 所以，A* 最优
• A* 图搜索最优？
  • 前提：一致性–就是可采纳性
    • h(A)<=实际，
    • 且h(A)-h©<=弧cost(一致性）
  • 采用一致的h（启发函数，所以
    1. f单调递增
    2. 对每个状态s，到达s最优的节点，优于次优
    3. 所以是最优的
  • 证明
    • 假定到达G* (最优值)的路径上某个n不能进入队列，因为某个具有相同状态且较差的n’先被扩展了
    • 找到树中最高的这个节点n
    • p是n的祖先，且n’出列时在队列里
    • f§<f(n)(递增
    • f(n)<f(n’)次优
    • p应该在n’之前被扩展
    • 矛盾
    • 得证先到达G*
• 比较：

算法名称	方向	最优
贪婪	快速地向目标方向扩展，	不一定能够得到最优解
UCS	所有方向等可能扩展	能够得到最优解
A*	朝着最优解方向扩展	能够得到最优解

3.局部搜索—与路径无关

• 全局搜索

  • 保留了所有的路径

• 局部搜索

  • 与路径无关
  • 只与最终状态有关
  • 优点
    • 内存要求小
    • 快
  • 缺点
    • 不完备
    • 不最优
  • 用于纯最优问题
  • 操作：改进单一选项，直至不能改变
  • 新的后继函数：局部改变

• $\Delta E=E(next)-E(now):\Delta E>0,接受$:

算法名称	算法策略	时间复杂度	空间复杂度	完备性	最优性
爬山法（如SGD)	1.任意位置起始，2.移动到最好的相邻位置，3.无最好则结束	-	-	（不完备）	无
模拟退火（从爬山法改进）	1.任意位置起始，2.移动到最好的相邻位置，3.不好的状态则以$e^{\Delta E/T}$概率接受	-	-	（不完备）	下降够慢，则最优
遗传算法	1.选最好的N个（基于适应度函数），2.这几个配对，并杂交，3.随机变异各串中的一个，重复	-	-	（不完备）	？

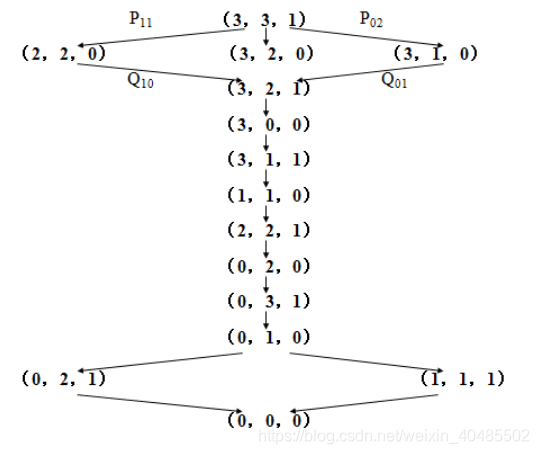
• M-左岸传教士数目
• C-左岸野人数目
• B-左岸是否有船
• Pcm-有c个传教士，m个野人从左岸到右岸
• Qcm-有c个传教士，m个野人从右岸到左岸
• 问题有解所必须的特性
  • M>=C且（3-M)>=(3-C)<==>M=C
  • 或者M=0,M=3
• 安全状态(以左岸为例)：
  1. 传教士与野人的数目相等；
  2. 传教士都在左岸；
  3. 传教士都不在左岸。
• 完全状态图：不满足约束的不在图内）
  *
  https://blog.csdn.net/guangheultimate/article/details/51377302