文章目录
- abstract
- 1.introduction
- 1.2 条件模型
- 2.标签偏差问题
- 3.CRF
- 提出条件随机场CRF
abstract
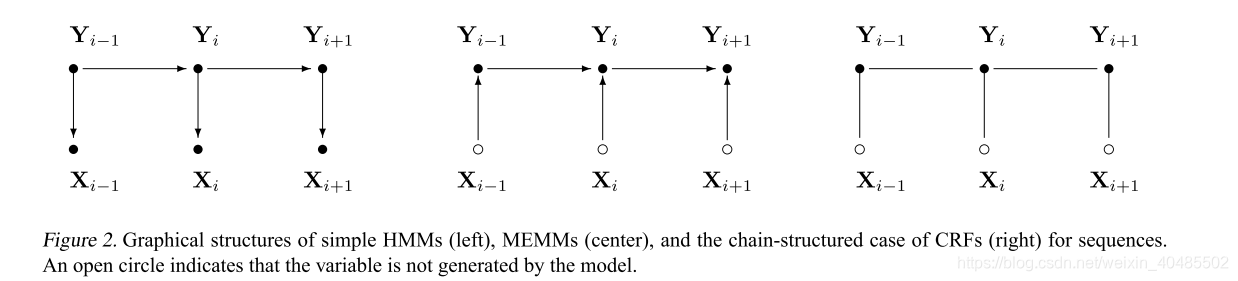
我们提出了条件随机场,这是一个建立概率模型来分割和标记序列数据的框架。相对于隐马尔可夫模型和随机语法,条件随机场在这类任务中有几个优势,包括能够放松这些模型中做出的强独立性假设。条件随机域也避免了最大熵马尔可夫模型(MEMMs)和其他基于有向图模型的判别马尔可夫模型的基本限制,这些模型可能会偏向于后继状态较少的状态。我们提出了条件随机场的迭代参数估计算法,并将得到的模型在合成和自然语言数据上与HMMs和MEMMs的性能进行了比较。
1.introduction
- 对序列进行分割和标记的需求出现在许多不同的问题中。隐马尔可夫模型(HMMs)和随机语法(stochastic grammars )是这类问题的常用概率模型。
- 生成模型
- 赋予成对观测序列和标记序列一个联合概率;
- 参数:最大化似然估计MLE
- 观察序列:单词–x
- 标注:词性/ner类型–y
- 困难:表示多个相互作用的特征或观测的长期依赖关系是不实际的
- 解决:条件模型
为了定义观察和标记序列的联合概率,生成模型需要枚举所有可能的观察序列,通常需要一个表示,其中的观察是适合任务的原子实体,如单词或核苷酸。特别是,表示多个相互作用的特征或观测的长期依赖关系是不实际的,因为此类模型的推理问题是棘手的。
这种困难是将条件模型作为备选方案的主要动机之一。条件模型指定给定观测序列的可能标签序列的概率。因此,它不会在观测上花费建模工作,因为在测试时观测是固定的。此外,标签序列的条件概率可以依赖于观察序列的任意的、非独立的特征,而不必强迫模型考虑这些依赖项的分布。所选的特性可能表示同一观察的不同粒度级别的属性(例如,英语文本中的单词和字符),或者观察序列的聚合属性(例如,文本布局)。标签之间转换的可能性不仅取决于当前的观察,而且取决于过去和未来的观察(如果可能的话)。与此相反,生成模型必须对观测结果做出非常严格的独立性假设,例如给出标签的条件独立性,以达到可处理性。
1.2 条件模型
-
条件模型:条件模型指定给定观测序列的可能标签序列的概率。
- 观测在测试时是固定的—x
- 标签序列的条件概率可以依赖于观察序列的任意的、非独立的特征,而不必强迫模型考虑这些依赖项的分布
- 特性
- 可以是不同粒度的
- 也可以是聚合属性
- 转移:依赖于过去/未来/x
- 无严格的独立性假设
-
最大熵马尔可夫模型(MEMMs)
- 是一种条件概率序列模型,它实现了上述所有优点(McCallum et al., 2000)。
- 在MEMMs中,每个源state1都有一个指数模型,该模型以观测特征为输入,并输出可能的下一个状态的分布。
- 采用适当的迭代标度法对MEMMs的这些指数模型进行训练
- 提高了回忆率(比HMM高一倍
-
MEMMs和其他基于下一状态分类器的非生成有限状态模型,如判别性马尔科夫模型(Bottou, 1991),
-
弱点:都有一个我们称之为标签偏差问题的弱点:离开给定状态的转换只会相互竞争,而不是与模型中的所有其他转换竞争。
在概率术语中,转换分数是给定当前状态和观察序列的可能下一状态的条件概率。这种每个国家过渡分数的标准化意味着分数质量的守恒(Bottou, 1991),因此到达一个国家的所有质量必须分配给可能的继承国。一个观测可以影响哪个目的地状态得到质量,但不影响传递的总质量。这导致了对输出转换较少的状态的偏爱。在极端情况下,具有单个传出转换的状态实际上忽略了观察结果。在这些情况下,与HMMs不同,Viterbi解码不能根据分支点之后的观察下调一个分支,并且具有状态转换结构的模型有稀疏连接的状态链没有得到适当的处理。MEMMs中的马尔可夫假设和类似的状态条件模型将一个状态下的决策与未来的决策隔离开来,但这种方式与连续状态之间的实际依赖关系并不匹配。
- CRFs
- 条件模型
- 解决标签偏差问题
- 区别:
- MEMM使用每个状态的指数模型来表示给定当前状态下的下一个状态的条件概率,而
- CRF使用单个指数模型来表示给定观察序列的整个标签序列的联合概率。
- 因此,不同状态下不同特征的权重可以相互抵消。
- 训练:最大似然或MAP估计进行训练
- 损失函数:是凸的,保证收敛到全局最优
- 可用于:随机上下文无关语法
- 有限状态模型,具有未归一化的转移概率
- 我们也可以认为CRF是一个有限状态模型,具有未归一化的转移概率。然而,与其他一些加权有限状态方法(LeCun et al.,
1998)不同的是,CRFs在可能的标签上分配了一个定义良好的概率分布,通过最大似然或MAP估计进行训练。此外,损失函数是凸的,保证收敛到全局最优。CRFs还可以很容易地推广到随机上下文无关语法的类似物,这将在RNA二级结构预测和自然语言处理等问题中很有用。- 提出了该模型,描述了两种训练方法,并给出了收敛性证明。我们还给出了合成数据的实验结果,表明CRFs解决了标签偏差问题的经典版本,更重要的是,当真实数据分布具有比模型更高的阶依赖性时,CRFs的性能优于HMMs和MEMMs,这在实践中经常出现。最后,我们通过在词性标注任务中对状态结构相同的HMMs、MEMMs和CRFs进行评价,证实了这些结果以及条件模型的优势。
- 本文成果
- 提出CRF(解决标签偏差)
- 两种训练方式及收敛性证明
2.标签偏差问题
-
存在此问题的:经典的概率自动机(Pa经典的概率自动机(Paz, 1971),判别马尔科夫模型(Bottou, 1991),最大熵标记器(Ratnaparkhi, 1996), MEMMs,以及非概率序列标记和分割模型与独立训练的下一状态分类器(Punyakanok &都是标签偏差问题的潜在受害者z, 1971),判别马尔科夫模型(Bottou, 1991),最大熵标记器(Ratnaparkhi, 1996), MEMMs,以及非概率序列标记和分割模型与独立训练的下一状态分类器(Punyakanok &都是标签偏差问题的潜在受害者
-
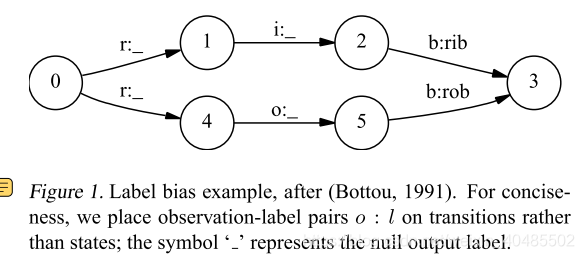
实例:例如,图1表示一个简单的有限状态模型,用于区分单词rib和rob。假设观测序列为rib,在第一个时间步中,r匹配开始状态的两个跃迁,因此概率质量在这两个跃迁之间的分布大致相等。接下来我们观察i,状态1和4都只有一个输出跃迁。状态1在训练中经常看到这种情况,状态4几乎从未看到过这种情况;但是和状态1一样,状态4别无选择,只能把它所有的质量传递给它唯一的向外的跃迁,因为它不是产生观测,而是对它进行调节。因此,只有一个外向过渡的国家实际上忽略了它们的观察结果。更一般地说,具有低熵的状态的下一个状态分布很少注意到观测结果。回到例子中,顶部路径和底部路径的概率是相等的,与观察序列无关。如果两个单词中的一个在训练集中稍微更常见一些,那么从起始状态转换出来的转换将稍微倾向于对应的转换,并且单词s状态序列将始终胜出。这一行为在第5节的实验中得到了证明。
-
解决方案
- L’eon Bottou(1991)讨论了标签偏差问题的两种解决方案。
- 一是改变模型的状态转换结构
- 在上面的例子中,我们可以折叠状态1和状态4,并延迟分支直到我们得到一个有区别的观察结果。这种操作是确定性的一个特例(Mohri, 1997),但是加权有限状态机的确定性并不总是可能的,即使有可能,也会导致组合爆炸。
- 提到的另一个解决方案是,从一个完全连接的模型开始,让训练过程找出一个好的结构。
- 但是,这将妨碍使用在信息提取任务中已被证明非常有价值的先前结构知识(Freitag & McCallu)
- 确的解决方案要求模型同时考虑整个状态序列,根据相应的观察结果,允许某些转换比其他转换更强烈地“投票”。
- 这意味着分数质量不会被保留,相反,个体的转变可以“放大”或“减弱”他们所接收到的质量。
- 在上面的例子中,转换从一开始状态会非常弱的影响路径的分数,尽管state1和4的过渡会更加强烈的影响,放大或衰减取决于实际的观察,占比大的对维特比选择贡献大。
在相关的工作部分中,我们讨论了其他的启发式模型类,它们全局地而不是局部地考虑状态序列。据我们所知,CRFs是唯一一个在纯概率设置下进行此操作的模型类,它具有全局最大似然收敛的保证
3.CRF
其中,X是待标号数据序列上的随机变量,Y是对应标号序列上的随机变量。假设Y的所有分量Yi都在一个有限的字母集Y上。例如,X可能在自然语言句子上取值,Y可能在这些句子的词性标记上取值,Y可能是一组词性标记。随机变量X和Y是共同分布的,但在判别框架中,我们根据成对观察和标记序列构造了条件模型p(Y |X),而没有显式地对边缘p(X)进行建模
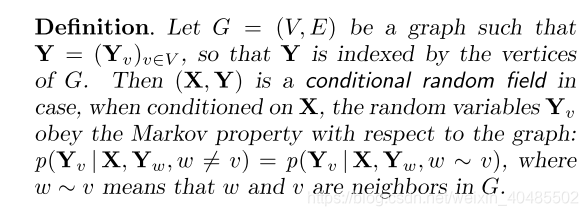

因此,CRF是基于观测x的全局随机场。在本文中,我们默认图G是固定的。以最简单最重要的方式
- 参数估计:
- 最大似然函数的目标函数
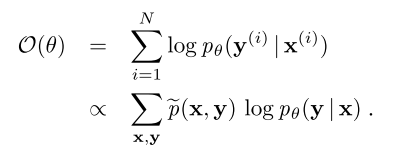
- 最大似然函数的目标函数
- 矩阵形式


- 训练方法
- improved iterative scaling (IIS) algorithm of Della Pietra et al. (1997)
- 问题:然而,有效地计算这些方程右边的指数和是有问题的,因为T(x, y)是(x, y)的一个全局性质,而动态规划将对具有潜在变化T的序列求和
- 改进
- 算法S(slack feature)
- 算法T(记录部分T总数)
- improved iterative scaling (IIS) algorithm of Della Pietra et al. (1997)


- 前向后向算法
- α1(x)={1y=start0otherwise\alpha_1(x)=\begin{cases}1& y=start\\0& otherwise\end{cases}α1(x)={10y=startotherwise

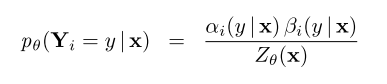
- 证明


)

)

)



)

2017)

)


)

)
