[完结]以C++与Java为例，详解数据结构的动态增长策略

前言

本文改编自小夕的订阅号文章《【萌味】小夕说,不了解动态空间增长的程序喵都是假喵（上）》、《【萌味】小夕说,不了解动态空间增长的程序喵都是假喵（中）》、《【萌味】小夕说,不了解动态空间增长的程序喵都是假喵（下）》。萌气已过滤，需要呼吸萌气的读者请戳上面原文哦。

笔者学了数据结构后，知道了链表、树、哈希表等数据结构与静态数组的固定容量不同，它们是可以动态添加元素的。这种数据结构的初始大小可能很小，甚至几乎为零，但是随着新元素的加入，其大小（内存空间占用）会不断增长，这个过程就叫做动态空间增长。

那么问题来了，所有支持动态空间增长的数据结构都是相同的增长方式吗？了解这个又有什么意义呢？

笔者曾经很傻很天真的认为所有支持动态空间增长的数据结构都是每增加一个元素，数据结构的大小就增加1个单位。直到在一个中规模机器学习任务的数据预处理过程中遇到了“内存爆炸”的问题，即笔者明明计算的内存够用，但是笔者可怜的电脑的内存却意外爆满了。这是怎么回事呢？

笔者为了避免讲解太过抽象，所以建议：如果您擅长C++，那么请注意一下Vector数据结构；如果擅长Java，请注意一下ArrayList、LinkedList、哈希系列(HashSet/ HashTable/ HashMap)；如果您不用Java也不用C++，或者已经脱离XX编程语言的层次，那么请注意一下可变数组（可增长顺序表）、链表、哈希（散列）。笔者将基于上述数据结构展开讲解。

递增式扩容

对于Java的LinkedList，也就是数据结构中的链表，其空间增长方式就是笔者一开始的设想：每增加一个元素，其大小就增加一个单位（这里的一个单位就是指一个元素占用的空间大小）。原因就在于链表在内存中的存储可以是不连续的。例如一个依次由节点1、节点2、节点3连接而成的链表在计算机内存中完全有可能是下面的存储方式。

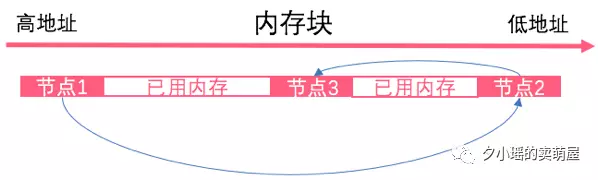
这样的话，链表每增加一个元素，只需要在内存中找个缝将新元素插进去就可以。所以如果笔者手里有n个元素想插入链表，则需要开辟n次内存，每次均开辟一个元素的大小。

这种数据结构建立后，每次数据结构要扩容时均增加固定空间大小的做法被称为【递增式扩容】。显然链表的空间增长方式就是递增式扩容，而且递增的单位为1（这里是指1个单位，即一个结点的大小）。

可以看到，如果是链表数据结构，或者是底层基于链表而实现的数据结构，采用递增式扩容是最优选择。因为要增加一个元素，则最好的情况就是其他什么都不动，仅仅是为该元素开辟一个单位的空间，然后塞入该元素。而递增式扩容用于链表确实达到了这个最理想情况呢。因此，对于链表，以及底层基于链表结构实现的数据结构，都是采用递增式扩容即可达到最优扩容效率（最优动态空间增长）。例如哈希中的横向增长，再如基于链表实现的树（如Java中的TreeSet，TreeMap等）。

因此在操纵大量数据的时候，尤其机器学习任务中常见的操纵大量样本的时候，在内存的问题上可以安心的使用此类数据结构，不会导致“内存爆炸”的问题，内存只会慢慢的起火然后轻轻的告诉你满了。当然了，不能仅考虑内存，有时操纵大量数据时对数据处理效率要求更高，这时候就要舍内存保速度啦。

那么哪些常见数据结构采用递增式扩容无法达到最优呢？它们有什么共性吗？还有，小夕遇到的内存爆炸是怎么回事呢？

源于数组

那么对于C++中的Vector，Java中的ArrayList、HashSet/ HashTable/ HashMap，也就是数据结构中的可变数组、哈希来说，空间增长方式是怎样呢？可能有读者此时在想“这些数据结构又不一样，怎么放到一起讨论了呢？”

其实这些表面看似不同的东西，底层的实现方式确是一样的，它们在底层都是通过操纵静态数组来实现他们的动态空间增长功能，下文会详细介绍。

讲到这里，可能有读者会记得笔者在上一篇中也提到过哈希，说哈希的横向增长是基于链表的，因此递增式扩容是最优动态空间增长方案。那这一篇中又说哈希是基于静态数组的，这是怎么回事呢？下面给没有接触过哈希的读者先科普一下哈希：

哈希的横向增长是基于链表实现的，即当新元素的哈希值与已有元素哈希值相同时，新元素会插入到某个链表中，因此是递增式增长。但是更多的情况下，哈希是纵向增长的。学过数据结构的宝宝知道，哈希在纵向上就是一个指针数组，数组的每个索引值即代表一个哈希值，数组的每个元素是一个指向某链表的指针。画个图来看就是这样的。

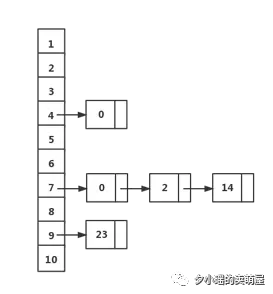
所以，在本篇文章中，我们不看哈希的横向增长，只关注纵向增长，此时显然是基于静态数组实现的。

基于数组的扩容原理

下面笔者直接以“数据结构”代称所有这些基于静态数组实现的动态空间分配的数据结构，包括但不限于上文提到的C++中的Vector（即数据结构中的动态数组），Java中的ArrayList（即动态数组）、Hash系列（即哈希/散列）等。

具体来说，如何用静态数组实现上述的动态空间增长的数据结构呢？其实很简单，每次数据结构要扩容时只需要依次进行下述操作就可以完成：

开辟一段新的内存空间，空间大小就是扩容后的数据结构大小。
把旧数据结构，也就是旧的内存空间的元素一个个的复制到新的内存空间
释放旧的内存空间（代码上就是删除旧空间的指针，当然像Java这种自动管理内存的语言就不用操心这一步了）

通过上述扩容的三步操作，可以看到每次哈希表的扩容操作的代价还是挺大的。第1步和第3步的代价不算大，但是第2步的代价会随着要搬移元素数量的增加而直线上升。所以这就相当于一个完整搬家的过程：先买个新房子，再把旧房子里的全部家当搬到新房子里去，再把旧房子注销。

加倍式扩容

既然代价如此之大，那么显然我们要尽量减小扩容次数。怎么扩呢？一个很creative的想法就是每次使数据结构变为自身的两倍！再机智一点，每次使数据结构变为自身的N倍！其中N只要大于1就可以！口说无凭，下面给出算法分析的过程。

假如数据结构A使用【递增式扩容】。每次数据结构满了的时候就固定的增加10个单位的空间（增加单位的数量不会影响最终分析出来的复杂度哦）。好，那小夕现在手里有n个元素想添加进数据结构，假如n的数值很大，远远的大于10，那么要执行多少次扩容操作呢？当然是n/10次啦~这n/10次扩容的累计开销大约为

$cost=10+2*10+3*10+...+(n/10)*10$

计算一下这个级数，就是

$cost=[(n/10)/2]*[(n/10)+1]*10$

所以复杂度是O( $n^2$ )的数量级，所以平均每个元素被添加进哈希表时的开销为cost/n，也就是O(n)的复杂度。

假如数据结构B使用【加倍式扩容】。每次数据结构满了的时候，数据结构的大小就变成原来的2倍（与之前同样的，这个倍数取不同的值并不会影响最终分析出来的复杂度,当然倍数必须大于1！）。同样，将n个元素添加进数据结构，假如n的数值很大，远远的大于2，那么要执行的扩容操作的次数是log2n！令c=log2n，则这c次扩容操作的累计开销为 $cost=2^1+2^2+...+2^c$

这个级数的和为

$cost=[2/(1-2)]*(1-2c)$

代入c=log2n得cost=2(n-1)。也就是说复杂度为O(n)，所以平均每个元素被添加进哈希表时的开销为cost/n，也就是O(1)的复杂度！注意前面我们计算过，这里数据结构A（递增式扩容）的复杂度为O(n)!

讲到这里读者应该清楚了吧？所以如果有一天你要自己写一个基于数组的动态空间增长的数据结构的话，可千万不要写成递增式扩容了。

内存爆炸

正是因为这类数据结构采用了加倍式扩容，导致这类数据结构申请内存的时候翻倍翻倍的要。结果当时在那个中规模机器学习任务中，笔者算的是一个超大哈希表只需要占用5个G作右的内存空间，而实际上在往这个哈希表加数据时，从4个G直接爆到了接近8个G，导致笔者内存8G的小电脑直接崩盘了。

等等，看似此文可以结了，实际上，敏锐的读者可能想到了：“递增式扩容你都告诉我了每次扩容增加一个单位的空间就最优了，那加倍式扩容每次增大几倍最优呢？”如果读者能发现这一点的话，真的非常棒啦！答案是2倍吗？当然不！那是几呢？真的有最优倍率吗？

一个视角：内存复用

如果倍率采用2甚至更大的数，那么被开辟过的旧空间永远都不会被新开辟的空间利用。小夕举个栗子。

if(倍率≥2){

那么以下是小夕为大家画的三次扩容后的内存块的占用情况

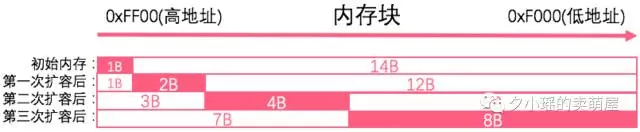
上图中，内存块一共有15个字节。粉色实心框是数据结构占用的内存块，空心框是空闲的内存。

假如一开始数据结构的大小是1字节，占用了0xFF00这个字节，如图中第一列。然后第一次扩容后数据结构大小变成2字节，无法利用之前的旧内存空间。

同样，第二次扩容，第三次扩容后，数据结构的大小总是要比之前累计占用的旧内存空间之和还要大，总是大1个字节，所以永远都无法重新利用之前的旧内存空间。

那么无法复用旧内存空间，对应有程序与操作系统各有什么影响呢？小夕还没有探索出严谨的结论，读者有思路可以跟小夕一起讨论哦~

如果倍率改为比2大的数，结果是一样的。有兴趣的读者可以自行画画图~当然，数学好的喵喵不用画图也能证明出来的~（利用几何级数的性质）

}

if(倍率<2&&倍率>1){

比如倍率采用1.5。小夕再画一下图~

可以看到，第三次扩容后的新数据结构大小约为338B！而旧空间的大小是250+225=475>338，也就是说新的哈希表可以挪到旧的内存空间了！内存得到了复用！

好咯，说到这里，读者应该懂了，对于加倍式扩容，倍率必须小于2才能复用内存。那么为什么默认值取1.5，而不是1.6，1.7呢？小夕查了很多资料，发现这是一个启发式策略（启发式策略就是拍脑袋想出来的看似合理而没有严谨理论依据的方法）。

一个疑问

那么既然看似倍率用1.5要优于2，为什么C++中部分Vector的实现中却采用2呢？

注：感谢@冒泡指正，有的C++中Vector的实现采用的1.5倍。

这就是理论与工程的不同之处。在工程中不仅要考虑内存复用这一个问题，还要考虑到浮点数运算问题和大量数据场景下的扩容速度的问题。

关于浮点运算：此处感谢@谢天奇指正，小夕之前想当然了，深深抱歉！浮点运算速度不会因有效位的增加而降低，但一般来说浮点运算效率确实比整型运算的效率低。因此确实存在浮点运算问题，但若采用浮点数运算，计算浮点数时的速度在理论上是几乎无变化的。

扩容速度也很好理解。大量数据时，2倍扩容速度会比1.5倍扩容速度少很多次扩容次数，因此效率会比1.5倍高很多。那么当程序不怎么看重内存复用，却有大量数据待填入数据结构时，2倍是更合理的。

补充：关于哈希的扩容倍率

该章节由@冒泡提供，对哈希的扩容倍率的考虑不在上一章节讨论范围内。哈希之所以采用2倍的扩容倍率（更准确的说哈希的扩容倍率应采用2的幂次），是处于哈希表元素找位置的角度考虑的。

下面引用@冒泡清晰的讲解：

一般来说，hash表元素找位置的办法是元素的hash值对表大小取模
理论上表大小是个正数就可以，不过对于一般的数字，计算机的整数除法是很慢的
如果表大小是2的幂，则可以用位运算来代替除法，比如表大小为1024，则K%1024可以优化为K&0x3FF，速度就快很多，所以hash表大小最好保持为2的幂，因此扩容时候只能乘以2，或乘以2的幂
因为这个原因，java的hash表扩容，才是翻两倍