2022年诺贝尔物理学奖的科学内涵辨识

|作者：葛惟昆

(清华大学物理系)

本文选自《物理》2022年第12期

摘要 2022年的诺贝尔物理学奖，被一些人误解为证明了量子纠缠现象。实际上，包括爱因斯坦本人都承认量子纠缠，关键在于如何诠释。今年诺贝尔物理学奖的价值在于这几位物理学家以无可争辩的实验事实，证明了基于定域隐变量的贝尔不等式是不对的。目前的一些介绍文字，没有认真解释量子力学在理论上是如何批驳贝尔不等式的，同时虽对量子纠缠的物理价值多有阐述，但对其哲学意义却鲜有评述，对社会上滥用纠缠概念缺少直接批判和阐释。文章希望在这两方面有所补充。

关键词 量子纠缠，EPR佯谬，贝尔不等式，物理与哲学

众望所归，如期而至，瑞典皇家科学院秘书长汉斯·耶利格林在10月4日宣布，将2022年诺贝尔物理学奖授予法国物理学家阿兰·阿斯佩(Alain Aspect)、美国理论和实验物理学家约翰·弗朗西斯·克劳泽(John F. Clauser)，以及奥地利物理学家安东·蔡林格(Anton Zeilinger)，如图1所示，以表彰他们在光子纠缠实验、贝尔不等式的颠覆和量子信息科学方面的开创性贡献。

图1 2022 年诺贝尔物理学奖得主 Alain Aspect，John F. Clauser，Anton Zeilinger

光子纠缠实验早已广为人知、闻名于世，甚至排进了大学本科的近代物理实验教学中^[1]。实验虽然堪称精巧，但并不十分复杂，认真的大学本科高年级学生和研究生都可以完成，也可以写出漂亮的实验报告。其中的理论推导部分也不十分艰深。然而真正理解这个实验的人并不多，大多数学生做了实验，也依然停留在知其然不知其所以然的朦胧状态。这当中的困惑，在于其逻辑推衍，这才是它的价值所在，是它的物理真谛。本文试图以简明清晰的方式予以解读，以飨一般读者。

这一发展的一个关键因素是量子力学如何允许两个或多个粒子以纠缠态存在(图2)。纠缠粒子对之中的一个粒子的状态，决定了另一个粒子的状态，即使这两个粒子相距很远——这就是“量子纠缠”，或说是“量子叠加态”。量子纠缠触及了对量子力学本质的理解、对自然规律的认识，以及量子理论未来的发展和第二次量子革命，也涉及了量子力学深刻的哲学内涵。

图2 量子纠缠示意图

故事要从头说起：为什么产生了这个实验，它的物理背景是什么？

EPR佯谬和贝尔不等式

众所周知，量子力学在几十年前曾受到包括物理学泰斗级人物爱因斯坦、薛定谔等多位物理学家的公开质疑，其中就包括了“量子纠缠”。爱因斯坦称，量子纠缠为“幽灵般的超距作用”。他还有一句针对玻恩几率解释的名言——“上帝不会掷骰子”。

近90年前的1935年，爱因斯坦和一位博士后罗森(N. Rosen)、以及研究员波多尔斯基(B. Podolsky)联合发表了论文《物理实在的量子力学描述能否被认为是完备的？》，后人称之为EPR文章，EPR即是三人姓名的首字母。这篇文章的论证又被称为“EPR佯谬”或“爱因斯坦定域实在论”，爱因斯坦认为，一个粒子只在局部拥有其所有特性并决定了任何测量的结局。

随后，薛定谔也发表了几篇相关论文，定义了“量子纠缠”这一术语。但量子纠缠这种行为被爱因斯坦抨击为违背定域实在论。他表示，量子力学的标准表述不具完备性。

1964年，英国物理学家约翰·贝尔(John Stewart Bell)提出了以他名字命名的数学不等式。他提出，如果存在隐变量，大量测量结果之间的相关性将永远不会超过某个值。然而，量子力学预言，某种类型的实验将违反贝尔不等式，从而导致比其他方式更强的相关性。

现在我们仔细来看EPR佯谬和贝尔不等式究竟在说什么。

1.1 EPR佯谬

EPR(Einstein，Podolsky and Rosen)文章^[2]是一篇基于思想实验和逻辑推理的雄文。这个思想实验就是一个复合粒子分裂为朝相反方向运动(以保证动量守恒)的两个粒子，当我们观测其中一个粒子的某个物理参数(例如自旋，虽然EPR文章并没有用自旋)，另一个粒子的相应参数就瞬时确定了。这并不违背相对论，因为并没有超光速的信息传输，在经典物理中，这也不是问题，例如两个粒子的动量显然相关，知其一，可知其二。但是在量子力学的诠释上，却产生了疑问。因为量子力学中一个粒子的状态是不确定的，只有在测量时，产生所谓“波函数坍塌”，我们才知道它处于何种状态，而这同时，另一个粒子也产生了波函数坍塌，因此这第二个粒子的状态也已经自然而然地确定了。

文章的题目：“Can quantum-mechanical description of physical reality be considered complete?”就极富挑战性，显而易见是从根本上质疑量子力学。这种质疑始于对物理实在的完备(complete)描述。文章认为：“当不存在对一个系统的任何干扰时，如果可以对它的一个物理量的值有确定(即概率为1)的计量，那么就可以认为：存在一个与之相对应的物理实在。爱因斯坦本人随即在给薛定谔的信中更明确地说明了所谓“完备”或“不完备(incomplete)”的涵义：“在量子力学中，用一个含坐标(或位形空间)的波函数ψ来描述一个系统的实际状态。其随时间的演变由薛定谔方程来决定。人们现在会非常乐于说：波函数ψ是一个对于实在系统实际状态的一对一的表达。而测量结果的统计性质完全是测量设备或过程所致。本工作中，我将论述关于对实在之完备描述的理论。如果这种诠释不成功，那么我就把这种理论描述称为‘不完备的’”。

基于这种观念，EPR文章分为两部分。第一部分集中于对一个粒子在一个空间坐标中的量子力学描述。他们假定该粒子由波函数ψ完备地描述，同时也采用概率诠释。假定ψ是算符A的本征函数，且本征值为a，这个在量子力学中称为可观测量A所取的值a即是确定的，相应的物理系统也就是实在的。但是当粒子状态不是A的本征态时，就不存在一个由A所描述的物理量的确定的值了。然后看动量的本征值P₀，认定这个粒子态的动量也是实在的。那么当一个粒子处于动量的本征态时，如果要问它的坐标(即位置)，结果如何呢？事实上，此时所有位置的概率相等，即完全不确定。在EPR看来，得到该粒子之位置的唯一途径，是做一次测量。然而测量就干扰了粒子系统及其状态，使其不再是动量的本征态。用量子力学的语言来说，当两个算符代表的是两个不对易的物理量(例如位置与动量)时，这两个量不能同时具有物理的实在性。

爱因斯坦执着于“定域论”，而这与量子力学的非定域性是矛盾的。如前所述，量子力学中一个粒子在测量中“波函数坍塌”的同时，另一个粒子也产生了波函数坍塌，因此这第二个粒子的状态也已经自然而然地确定了。

具体来说，EPR文章之第一部分涉及两个命题：

(1)用波函数描述实在是完备的；

(2)当代表两个物理量的算符不对易时，这两个物理量同时具有实在性。

EPR的结论是，这两者一定有一个是伪命题。这就意味着，EPR文章做了一个看起来理所当然的“定域性”：一个粒子的属性只局域在这个粒子上，而此处所发生的，必须经过在空间中的传播，才能对彼处发生影响。量子纠缠显然突破了这个“定域性”的假说，因此被爱因斯坦称为“幽灵般的超距作用”。

当然，如果此处与彼处的两个粒子间有某种“隐变量”把他们勾连起来，那也就无所谓超距了，它们有着某种内在的关联，即隐变量，只是我们不知道这种隐变量究竟是什么，以及它如何勾连这两个粒子。隐变量的概念是大卫·玻姆(David Bohm)提出的，他把电子想象成本质上是经典的粒子，但以它为中心发出一种量子势场(quantum potential)，这种势场弥漫在整个宇宙中，使之可以感知周围的环境。与测量仪器发生互动的就是这个势场，它带来电子本身的变化。

约翰·贝尔赞成这个观念，他想以一种数学的方式证明隐变量的真实性，这就是贝尔不等式的由来。贝尔不等式表明，如果隐变量确实存在，那么一个关联函数必定不能超过某一确定的数值。而这个关联函数是可以实验测定的，所以贝尔不等式就成为一块“价值连城”的试金石，可以用来判断量子纠缠的真伪和来源，判断量子力学是否正确。

1.2 贝尔不等式

贝尔不等式是一个悖论。它的初衷就是用来辨别真伪的。贝尔本人倾向于爱因斯坦与玻姆的“隐变量”假说。按照隐变量的观念，纠缠粒子出生伊始，即已携带相同的基因，即隐变量。这个隐变量使它们互相关联，如同孪生兄弟姐妹之间的心灵感应，就基于他们分享相同的遗传基因。贝尔不等式本意是以数学的方式证实这个隐变量的存在，也间接地证明经典的解释是正确的，量子力学的诠释是不成立的。这里数学是简单的，逻辑却很深刻和烧脑。这部分内容请参阅张天蓉2015年在《物理》杂志上形象而准确的解释^[3]。

这个解释是关于粒子自旋的。自旋是基本粒子，包括光子和电子的一个基本属性，基本粒子依照它们的自旋为整数或半整数而被分类为玻色子和费米子，并服从不同的统计规律。对于EPR文章中假定的纠缠粒子对A和B，它们的自旋总处于相反的方向。在三维直角坐标系中，两个粒子的自旋分别有三个分量，总共有2³=8种可能的结合(不要与8个卦限相混淆)，以一个序数L来表示，并产生4种相关函数P_ij(L)，i、j代表x，y，z。对应每一个序数，都会有特定的值：+1表示可能存在，-1表示不可能存在，这个值也就是在求和时相应概率的系数。总概率则为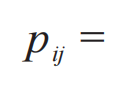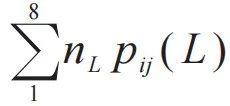：。经过一系列演算，可以得到：

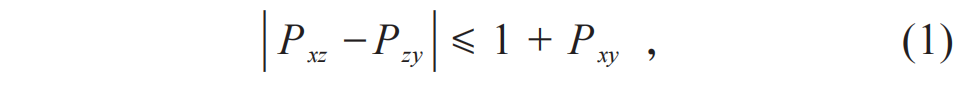
这就是名垂青史的贝尔不等式。名垂青史绝非夸大之词。当贝尔在62岁英年早逝时，很可惜他不知道当年自己已经被提名诺贝尔物理学奖。而今因他的启迪而诱导了精彩的实验研究，并众望所归地荣获了2022年诺贝尔物理学奖。他以一个批判者的角度，对量子力学原理的确立建立了不朽的功勋。

1.3 贝尔不等式如何与量子力学冲突？

贝尔不等式基于隐变量的假定，或对于粒子的经典描述，与隐变量的具体形式无关。为什么量子力学与贝尔不等式相悖呢？在樱井(J. J. Sakurai)著名的《现代量子力学》^[4]中给出了详尽的证明。他从两个观察者A和B，两个粒子1和2，及三个单位矢量a，b，和c开始，三个矢量一般并不正交。

根据量子力学中自旋单重态的表达式：

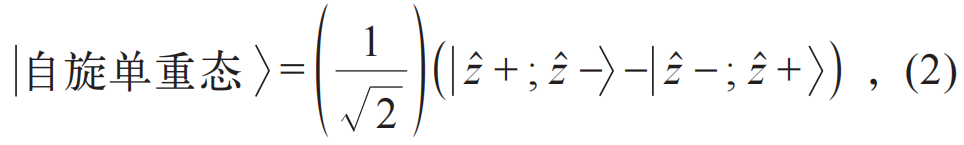
和量子力学运算法则，我们可以得出

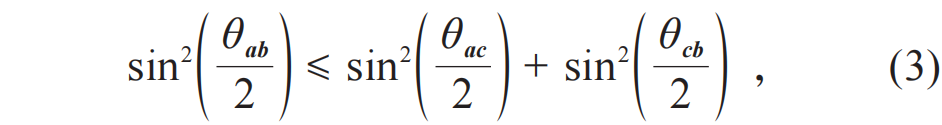
这里θ是矢量间夹角，其下角标是相应的矢量。当然从几何的角度来看，(3)式并不总是可能的。简单来说，我们把a，b和c设置在同一平面里，并使c居于a和b之间，即

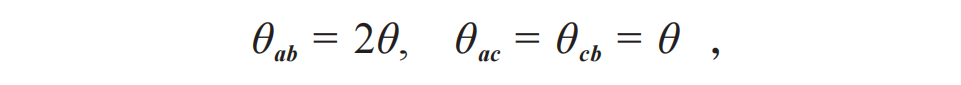
这样(3)式的不等式关系就在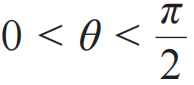的条件下被破坏了。举例来说，最极端的情况发生在θ=π/4，此时(3)式的左方为0.5，而右方为0.292，贝尔不等式被严重地违背了。也就是说，量子力学的预言与根据爱因斯坦的局域化原理所推导出来的贝尔不等式不相符。而且在实验上可以定量地验证这一点。

CHSH公式与光子纠缠实验

这一节需要量子力学的基本知识，我们借助于清华大学实验物理教学中心的“量子纠缠”实验讲义^[1]的介绍。

为了使实验更加现实，1969年，J. F. Clauser，M. A. Horne，A. Shimony和R. A. Holt改进并推广了贝尔不等式，形成所谓CHSH判据^[1]。

设4个测量方向分别为a，a′，b，b′，则关联函数P满足关系式：

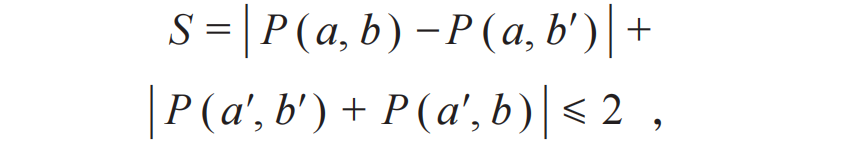
此式叫做CHSH不等式，它是贝尔不等式的一种。第一个检验CHSH不等式的实验是1972年Freedman和Clauser用原子级联辐射做出的。此外还有很多使用原子级联辐射检验CHSH不等式的实验，大多数的实验结果都支持量子力学，其中最著名的实验就是1981年Aspect，Grangier和Roger做的实验，该实验结果与量子力学符合得更好，以40倍标准偏差破坏贝尔不等式。

清华大学和北京大学都开设了量子纠缠的近代物理本科实验。实验利用BBO晶体参量下转换产生的双光子偏振纠缠态的相关性计算CHSH不等式中S的值：

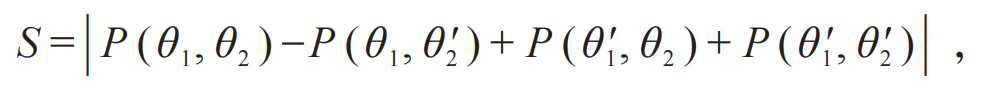
其中θ₁，θ₂，θ₁′，θ₂′分别为4个不同的偏振片角度，关联函数P(θ₁，θ₂)表示为符合计数的关系式：

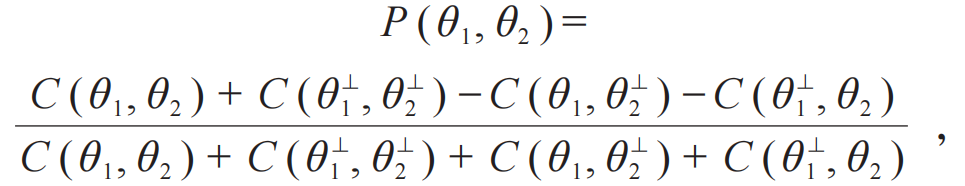
式中C(θ₁，θ₂)为A，B两路偏振片分别为θ₁和θ₂时的符合计数，C(θ₁^⊥，θ₂^⊥)为A，B两路偏振片分别取θ₁+90°和θ₂+90°时的符合计数。S≤2为基于定域实在论的结论，而特殊角度下量子力学给出的S最大可以为。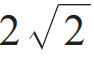

实验上对于贝尔(CHSH)不等式的测量和验证是对量子力学是否具有完备性的最有力的说明。CHSH不等式的实验检验无论是对量子力学基本原理的检验方面还是对量子信息安全性的保证方面都有重要意义。

量子纠缠究竟是什么？

被爱因斯坦称之为“幽灵般的超距作用”的量子纠缠，究竟是何方神圣？

量子纠缠的现象已经被实验证实，爱因斯坦及其合作者也并不怀疑这一点，但是它的实质尚在理解之中。目前的结论只是说它有的效应不能用经典理论或隐变量假说来诠释，但是符合量子力学的认知。如今它不但是一个物理问题，也是一个哲学问题，是大众关切的热点话题。诸如心灵感应，灵魂物质化的各种议论纷纷出炉，一时间“纠缠”的名词风靡全球，实实在在地纠缠着广大民众的心思。

量子纠缠究竟是什么？从物理实验的角度，我们已经了解，就是基于同源的两个(或多个)微观粒子间物理参量的自然关联。问题是，纠缠的本质是什么？它是如何造成，并且意味着什么？

要回答这个问题，必须承认微观世界与宏观世界服从不尽相同的物理规律，量子力学的所谓“神秘”和不可理解也正在于此。因为人类是属于宏观世界的，我们的认知以宏观世界为基础。人类无法“身临其境”地去了解微观世界的奥妙，只能通过各种测量手段去探索，而这无形中就以宏观世界的手段“干预”了微观世界，造成所谓的量子态的坍塌。从微观到宏观所发生的物理规律的变化，其实在凝聚态物理中早已体现。凝聚态物理的鼻祖安德森有一句名言“More is different”(多或大，会造成变化)，量变引致质变，就是凝聚态物质由众多的原子分子组成，但由于是众多原子分子的集合、凝聚，它的物理规律已然不同。最简单的例子，就是固体中的本征能级已经是连续的，而不像原子分子中那样是分立的。

而从宏观世界到微观世界，我们也可以说“Less is different”(少或小，会造成变化)。这个变化更加基本，催生了量子力学。量子力学最基本的原理，就是微观粒子的波粒二象性。量子纠缠就是微观世界粒子间本征的关联，是波粒二象性、波函数叠加，以致非定域性的自然结果。波粒二象性的基本表示就是德布罗意波长：

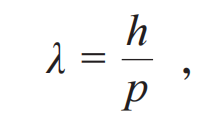
其中λ就是德布罗意波长，h是普朗克常数，p是物体(比如粒子)的动量。如果硬要把它套用到宏观物体上，那么我们可以看到，所得的德布罗意波长是无穷小，失去任何实际意义。再比如在宇观世界，必须用广义相对论做出正确的解释和定量的分析，这并不表明广义相对论不适于我们通常的宏观世界，只是在后者的尺度下，广义相对论与牛顿力学在定量分析上的差别完全可以忽略。尺度在这里是判据。这是又一种量变到质变的印证。

量子世界最本质的区别于宏观世界的现象是波粒二象性和状态的叠加性。量子纠缠的前提就是以叠加态来描述一个粒子。并非所有微观粒子之间都互相纠缠，纠缠粒子需要“生成”，基本上就是“一分为二”，如下转换晶体实验所出现的。所以在某种意义上，纠缠的粒子本来就是一体，或是一个整体的两种表现，而这两种表现是相互依存的。宏观地解释，就如同一枚硬币之两面，它们是一个整体，不可分割。这种整体的认识，反映了量子体系作为叠加态的本质，也是一分为二的普遍现象的微观表征。但是也有人无限夸大这种整体性，妄言整个宇宙是一个整体，所以似乎事事处处都有纠缠，世间万物都是纠缠的。这纯粹是对量子力学的无知。

量子纠缠是微观世界自然的现象，虽然可以表现在玻色—爱因斯坦凝聚、激光、超流等宏观现象中，特别是目前讨论的粒子非定域性^[5]。现在人们滥用“纠缠”一词，夸大或误解为普遍现象，试图解释许多匪夷所思的超距、超现实的现象，一些大量流传的视频，出于一些没有物理学，特别是没有量子力学基础知识的年轻人，造成很大的混乱。量子纠缠蕴含着丰富的哲学内涵。波粒二象性和叠加态，就是事物内部的对立统一，而从宏观到微观的规律演变，就是量变到质变的精彩演绎。量变是质变的必要准备；质变是量变的必然结果。质变是量变的必然结果，也为新的量变开辟道路，是事物在新质的基础上开始新的量变，循环往复，螺旋式上升。这正是辩证法的真谛。黑格尔在他的《逻辑学》中对量变质变的论证，以简单的化学为例证，比如从通常的氧O₂增加一个原子成为臭氧O₃，发生了性质的变化。恩格斯在引用黑格尔的理论时，更以周期表元素的变化，说明元素的变化基于其原子量的变化，显得更有说服力。到了量子力学的时代，我们看到的是从宏观到微观的革命性变化。而量子纠缠标志着量子力学正在经历第二次革命，在更深层次上揭示微观世界非定域性和状态叠加性这样一些基本事实背后的机制或原理。量子力学的第一次革命，已经成为现代科学技术发展的出发点，我们有理由期待它的第二次革命给世界带来崭新的面貌，给人类带来更大的福祉。

致谢 感谢《返朴》在完稿之初对文字的部分编辑。

参考文献

[1] 葛惟昆，王合英主编 . 近代物理实验 . 北京：清华大学出版社，2021

[2] Einstein A，Podolsky B，Rosen N. Physical Review，1935，47：777

[3] 张天蓉. 物理，2015，44(1)：44

[4] Sakurai J J. Modern Quantum Mechanics，Revised Edition. Addison Wesley，Longman，1994

[5] Davies P W，Brown J R. The Ghost in the Atom. Cambridge University Press，1986

2022年诺贝尔物理学奖专题

量子力学佯谬及第二次量子革命

《物理》在淘宝店和微店上线，扫码即可购买过刊和现刊。