题目链接：https://leetcode-cn.com/problems/climbing-stairs/

之前在递归中讲过这个问题，现在用动态规划求解。

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？
注意：给定 n 是一个正整数。

用dp[i] 表示到达第i个台阶的走法，那么到达第n个台阶的这个状态的走法，只跟n-1和n-2的状态有关（走1步或2步到n）
状态方程为 dp[n] = dp[n-1] + dp[n-2]

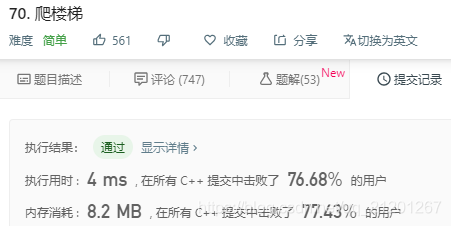
class Solution {
public:int climbStairs(int n) {if(n == 1)return 1;if(n == 2)return 2;int dp[n];dp[0] = 1;dp[1] = 2;for(int i = 2; i < n; ++i){dp[i] = dp[i-1] + dp[i-2];}return dp[n-1];}
};

对上面程序进行状态压缩，前面用不到的状态不保留

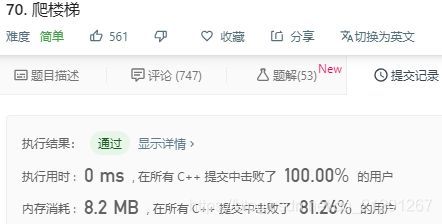
class Solution 
{
public:int climbStairs(int n) {if(n == 1)return 1;if(n == 2)return 2;int dp_i, dp_i_2 = 1, dp_i_1 = 2;for(int i = 2; i < n; ++i){dp_i = dp_i_1 + dp_i_2;dp_i_2 = dp_i_1;dp_i_1 = dp_i;}return dp_i;}
};