前言:模拟退火(simulated annealing)技术,在每一步都以一定的概率接受比当前结果更差的结果,从而有助于“跳出”局部极小。在每次迭代过程中,接受“次优解”的概率要随着时间的推移而逐渐降低,从而保证算法的稳定性。
嘻嘻嘻,推荐一篇好文章让你快速学习模拟退火算法求解旅行商问题
作者用的是c++编写的程序,而且作者在程序中设置的是每个城市的坐标,也就默认city a 到city b的距离和city b 到city a的距离一样了,和老师题目要求的用非对称矩阵来描述城市之间的距离是不一样的。
下面我参考作者代码,按老师的要求(A-B的距离不等于 B-A的距离)用 python 实现了TSP问题,其中参数也调了调。
不得不说,python真是个简单便捷的语言呢!!!
'''
设有n个城市和距离矩阵D=[dij],
其中dij表示城市i到城市j的距离,i,j=1,2 … n,
则问题是要找出遍访每个城市恰好一次的一条回路并使其路径长度为最短。
'''from time import time
from copy import copy
from numpy import exp
import numpy as np
import randomT0 = 10.0 # 初始温度
T_end = 0.001 # 最低温度
q = 0.98 # 退火系数
L = 10 # 每个温度时的迭代此时,即链长
N = 5 # 城市数量
city_list = [i for i in range(N)] # 初始化一个解
city_dis = np.floor(10 * np.random.random((N, N)) + 1) # 城市之间的距离矩阵# 计算路径长度
def path_len(path_list):path = 0for i in range(len(path_list) - 1):city1 = path_list[i]city2 = path_list[i + 1]dis = city_dis[city1][city2]path += dislast_city = path_list[-1]first_city = path_list[0]dis = city_dis[last_city][first_city]path += disreturn path# 采用随机交换位置的方式产生新解
def create_new():pos1 = random.randint(0, N - 1) # randint闭区间pos2 = random.randint(0, N - 1)temp = city_list[pos1]city_list[pos1] = city_list[pos2]city_list[pos2] = tempif __name__ == '__main__':t1 = time()count = 0 # 记录降温次数T = T0city_list_copy = [] # 保存原始解while T > T_end: # 当温度低于结束温度时,退火结束for i in range(L):city_list_copy = copy(city_list) # 复制数组create_new() # 产生新解f1 = path_len(city_list_copy) # 初始解目标函数值f2 = path_len(city_list) # 新解目标函数值df = f2 - f1# Metropolis 准则if df >= 0:print("df:", df)print("exp:", exp(-df / T))if exp(-df / T) <= random.random(): # 保留原来解city_list = copy(city_list_copy)T *= q # 降温count += 1t2 = time()print("城市之间的距离矩阵:\n", city_dis)print("模拟退火算法,初始温度T0=%.2f,降温系数q=%.2f,每个温度迭代%d次,共降温%d次\n" % (T0, q, L, count))print("TSP最优路径为:", city_list)print("最优路劲长度为:%1f\n" % (path_len(city_list)))print("程序耗时:%1f秒\n" % (t2 - t1))
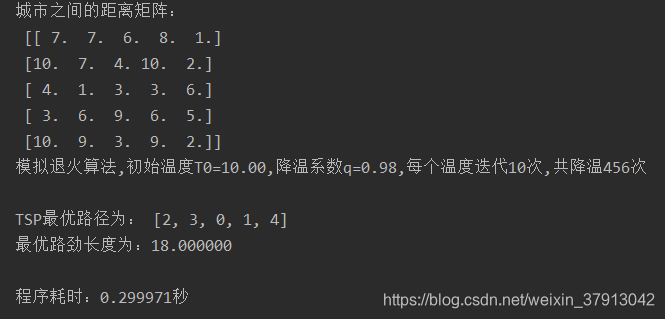
结果:
















,并使用。)


