为了加速数据库中数据的查找速度，我们常对表中数据创建索引。数据库索引是如何实现的呢？底层使用的是什么数据结构和算法呢？

1. 定义清楚问题

如何定义清楚问题呢？除了问题调研，还可以对一些模糊的需求进行假设，来限定要解决的问题的范围。

假设要解决的问题，只包含两个常用的需求：

• 根据某个值查找，比如 select * from user where id = 1234
• 根据区间来查找，比如 select * from user where id > 1234 and id < 2345

非功能性需求，比如安全、性能、用户体验等等。性能方面，主要考察时间和空间两方面，就是执行效率和存储空间。

• 在执行效率方面，希望通过索引，查询数据的效率尽可能的高；
• 在存储空间方面，希望索引不要消耗太多的内存空间。

2. 尝试学过的数据结构解决问题

支持快速查询、插入等操作的动态数据结构，已经学过散列表、平衡二叉查找树、跳表。

• 散列表。散列表的查询性能很好，时间复杂度是O（1）。但是，散列表不支持按照区间快速查找数据。
• 平衡二叉查找树。尽管平衡二叉查找树查询的性能也很高，时间复杂度是O（log n）。对树进行中序遍历，还可以得到一个从小到大有序的序列，但不足以支持按照区间快速查找数据。
• 跳表。跳表是在链表之上加上多层索引构成的。它支持快速地插入、查找、删除数据，对应的时间复杂度是O（log n）。并且，跳表也支持按照区间快速地查找数据。只需要定位到区间起点值对应在链表中的结点，然后从这个结点开始，顺序遍历链表，直到区间终点对应的结点为止。
  

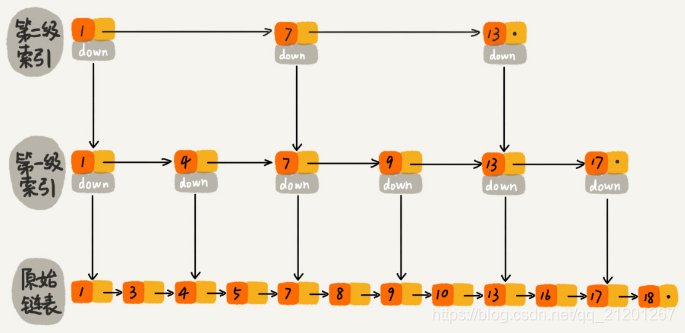
这样看来，跳表是可以解决这个问题。实际上，数据库索引所用到的数据结构跟跳表非常相似，叫作B+树。不过，它是通过二叉查找树演化来的。

3. 改造二叉查找树来解决问题

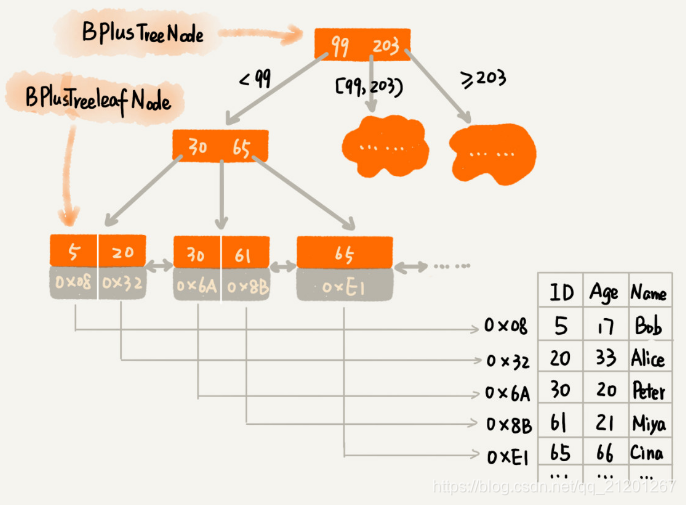
为了让二叉查找树支持按照区间查找数据，对它进行改造：树中的节点并不存储数据本身，而是只是作为索引。除此之外，我们把每个叶子节点串在一条链表上，链表中的数据是从小到大有序的。

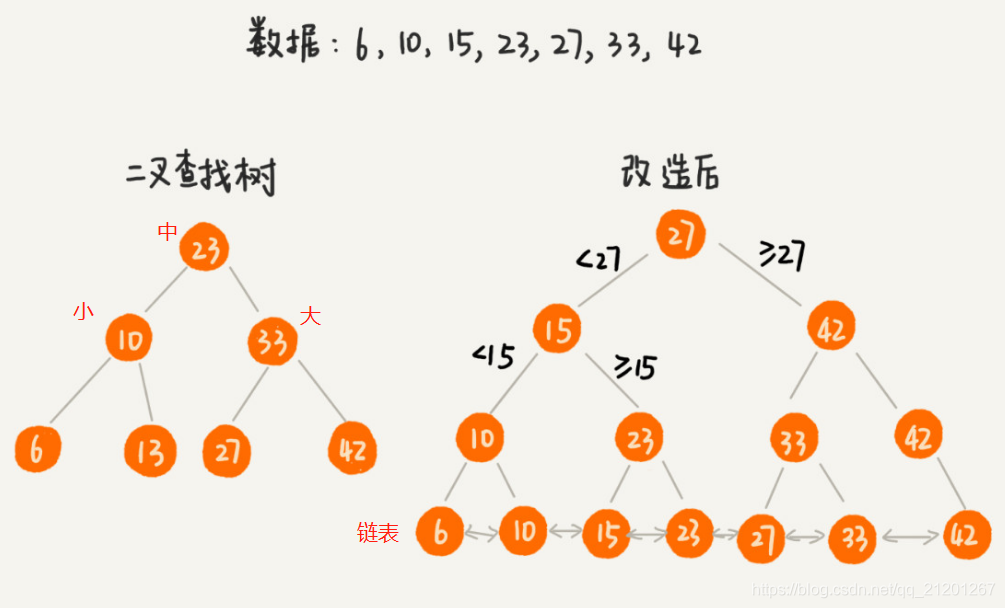
改造后，要查某个区间的数据。只需拿区间的起始值，在树中进行查找，当查找到某个叶子节点之后，再顺着链表往后遍历，直到链表中的结点数据值大于区间的终止值为止。所有遍历到的数据，就是符合区间值的数据。

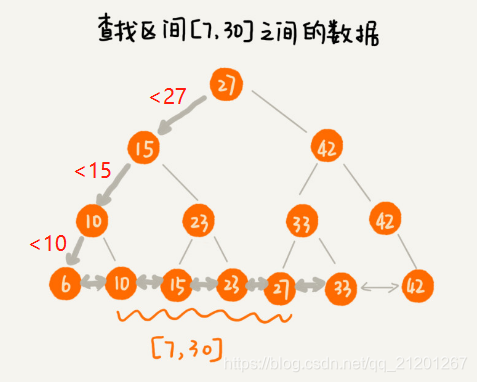
但是，要为几千万、上亿的数据构建索引，将索引存储在内存中，尽管内存访问速度非常快，查询效率非常高，但是，占用的内存非常多。

比如，给一亿个数据构建二叉查找树索引，索引中大约1亿个节点，每个节点假设占用16个字节，要大约1GB的内存。给一张表建立索引，需要1GB的内存。如果要给10张表建立索引，那对内存的需求是无法满足的。如何解决这个索引占用太多内存的问题呢？

可以借助时间换空间的思路，把索引存储在硬盘中，而非内存中。硬盘非常慢。通常内存访问纳秒级，而磁盘访问毫秒级。将索引存储在硬盘中，尽管减少了内存消耗，但是数据查找，需读取磁盘中的索引，因此查询效率降低很多。

二叉查找树，经过改造之后，支持区间查找的功能就实现了。节省内存，把树存储在硬盘中，每个节点的读取（或者访问），对应一次磁盘IO操作。树的高度就等于每次查询数据时磁盘IO操作的次数。

所以优化的重点就是尽量减少磁盘IO操作，也就是， 尽量降低树的高度 。如何降低树的高度呢？

如果把索引构建成m叉树，高度是不是比二叉树要小呢？
如图所示，给16个数据构建二叉树索引，树的高度是4，查找一个数据，就需要4个磁盘IO操作（如果根节点存储在内存中，其他结点存储磁盘），
如果对16个数据构建五叉树索引，那高度只有2，查找一个数据，对应只需要2次磁盘操作。
如果m叉树中的m是100，那对一亿个数据构建索引，树的高度也只是3，最多3次磁盘IO就能取到数据。磁盘lO少了，查找效率也就高了。

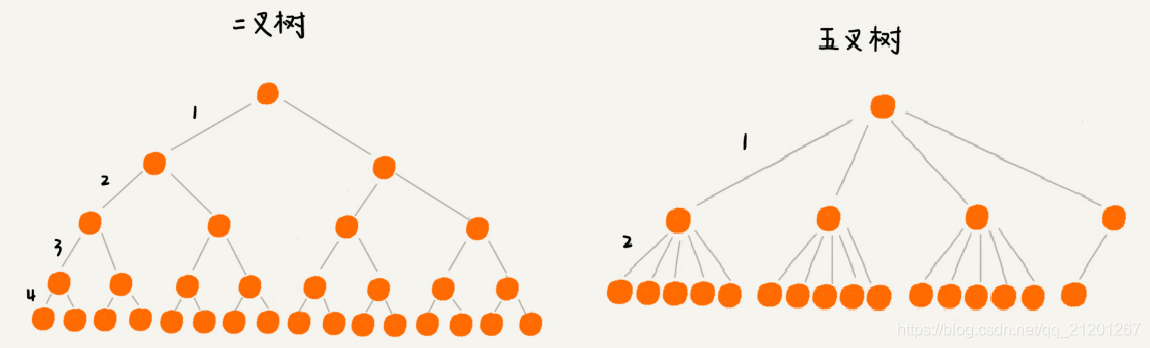
m叉树中的m越大，那树的高度就越小，那m叉树中的m是不是越大越好呢？多大才最合适？

不管是内存数据，还是磁盘数据，操作系统都是按页（一页大小通常是4KB，这个值可以通过 getconfig PAGE_SIZE命令查看）来读取的，一次会读一页的数据。如果要读取的数据量超过一页的大小，就会触发多次IO操作。所以，我们在选择m大小的时候，要尽量让每个节点的大小等于一个页的大小。读取一个节点，只需一次磁盘IO操作。

尽管索引提高数据库查询效率，索引有利也有弊，它也会让写入数据的效率下降。这是为什么呢？

数据写入过程，会涉及索引的更新，这是主要原因。

对于B+树来说，m值是根据页的大小事先算好的，也就是说，每个节点最多只能有m个子节点。往数据库写入过程中，有可能使某些节点的子节点个数超过m，这个节点的大小超了一个页的大小，读取这个节点，就会导致多次磁盘IO操作。该如何解决？

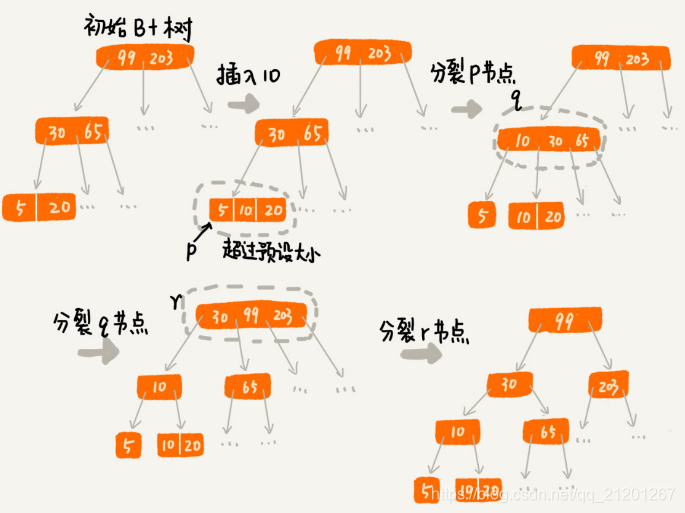
处理思路并不复杂。只需将这个节点分裂成两个节点。但是，节点分裂之后，上层父节点的子节点个数可能超过m个。用同样的方法，将父节点也分裂成两个节点。这种级联反应会从下往上，一直影响到根节点。

这个分裂过程，可以结合下图，会更容易理解（图中的B+树是一个三叉树。限定叶子节点中，数据个数超过2个就分裂节点；非叶子节点中，子节点的个数超过3个就分裂节点）。

因为要时刻保证B+树索引是一个m叉树，索引的存在会导致数据库写入速度降低。删除数据也会变慢。为什么呢？

删除数据时，也要更新索引节点。频繁删除，导致某些结点中，子节点个数变得非常少，长此以往，如果每个节点的子节点都比较少，势必会影响索引的效率。

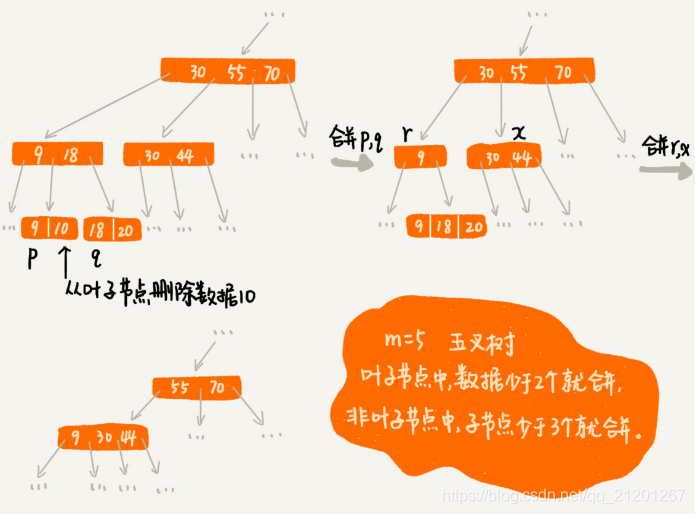
可以设置一个阈值。在B+树中，这个阈值等于m/2。某个节点的子节点个数小于m/2，将它跟相邻的兄弟节点合并。不过，合并之后结点的子节点个数有可能会超过m。再分裂节点。

文字不直观，举个删除例子，（图中的B+树是一个五叉树。限定叶子节点中，数据少于2个就合并节点；非叶子节点中，子节点少于3个就合并）

B+树的结构和操作，跟跳表非常类似。理论上，对跳表稍加改造，也可以替代B+树。

4. 总结

• 数据库索引实现，依赖的底层数据结构，B+树。
• 通过存储在磁盘的多叉树结构，做到了时间、空间的平衡，既保证了执行效率，又节省了内存。

总结一下B+树的特点：

• 每个节点中子节点的个数不超过m，也不小于m/2；
• 根节点的子节点个数可以不超过m/2，这是一个例外；
• m叉树只存储索引，并不存储数据，这个有点儿类似跳表；
• 通过链表将叶子节点串在一起，可以方便按区间查找；
• 一般情况，根节点会被存储在内存中，其他节点存储在磁盘中。

简单提一下。
B- 树就是B树，英文翻译都是B-Tree，这里的 “-” 不是相对B+树中的“+”，只是一个连接符。这个很容易误解。

B树实际上是低级版的B+树，或者说B+树是B树的改进版。B树跟B+树的不同点主要集中在这几个地方：

• B+树中的节点不存储数据，只是索引，而B树中的节点存储数据；
• B树中的叶子节点并不需要链表来串联。

也就是说，B树只是一个每个节点的子节点个数不能小于m/2的m叉树。