1. 比赛结果

2019.9.24晚，第一次参加线上比赛
比赛排名结果：582/1541，做出了2道题。。。

我证明了：我不是最菜的！！！

2. 题目解析

---

2.1 猜数字 Easy

小A 和 小B 在玩猜数字。小B 每次从 1, 2, 3 中随机选择一个，小A 每次也从 1, 2, 3 中选择一个猜。他们一共进行三次这个游戏，请返回 小A 猜对了几次？

输入的guess数组为 小A 每次的猜测，answer数组为 小B 每次的选择。guess和answer的长度都等于3。

示例 1：
输入：guess = [1,2,3], answer = [1,2,3]
输出：3
解释：小A 每次都猜对了。示例 2：
输入：guess = [2,2,3], answer = [3,2,1]
输出：1
解释：小A 只猜对了第二次。

限制：
guess的长度 = 3
answer的长度 = 3
guess的元素取值为 {1, 2, 3} 之一。
answer的元素取值为 {1, 2, 3} 之一。

---

送分题目，不解释，只是一开始觉得这么简单，会不会坑我

class Solution {
public:int game(vector<int>& guess, vector<int>& answer) {int count = 0;for(int i = 0; i < 3; ++i){if(guess[i] == answer[i])++count;}return count;}
};

---

2.2 分式化简 Esay

有一个同学在学习分式。他需要将一个连分数化成最简分数，你能帮助他吗？

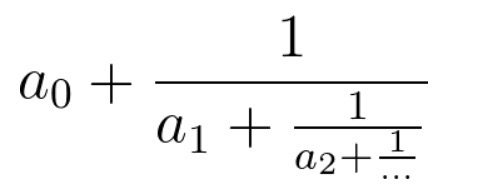
连分数是形如上图的分式。在本题中，所有系数都是大于等于0的整数。

输入的cont代表连分数的系数（cont[0]代表上图的a0，以此类推）。返回一个长度为2的数组[n, m]，使得连分数的值等于n / m，且n, m最大公约数为1。

示例 1：
输入：cont = [3, 2, 0, 2]
输出：[13, 4]
解释：原连分数等价于3 + (1 / (2 + (1 / (0 + 1 / 2))))。注意[26, 8], [-13, -4]都不是正确答案。示例 2：
输入：cont = [0, 0, 3]
输出：[3, 1]
解释：如果答案是整数，令分母为1即可。限制：
cont[i] >= 0
1 <= cont的长度 <= 10
cont最后一个元素不等于0
答案的n, m的取值都能被32位int整型存下（即不超过2 ^ 31 - 1）。

---

• 数学递推公式推导
• 用up表示初始分子（1），down表示初始分母（最后一个系数）
• 递推公式 $up=down\ast a_i+up$
• 然后颠倒分子分母
  

class Solution {
public:vector<int> fraction(vector<int>& cont) {int up = 1, down = cont.back(), i;for(i = cont.size() - 1; i >= 1; --i){up = down*cont[i-1]+up;swap(up, down);}return {down, up};}
};

---

2.3 机器人大冒险 Medium

力扣团队买了一个可编程机器人，机器人初始位置在原点(0, 0)。小伙伴事先给机器人输入一串指令command，机器人就会无限循环这条指令的步骤进行移动。指令有两种：

U: 向y轴正方向移动一格
R: 向x轴正方向移动一格。
不幸的是，在 xy 平面上还有一些障碍物，他们的坐标用obstacles表示。机器人一旦碰到障碍物就会被损毁。

给定终点坐标(x, y)，返回机器人能否完好地到达终点。如果能，返回true；否则返回false。

示例 1：
输入：command = "URR", obstacles = [], x = 3, y = 2
输出：true
解释：U(0, 1) -> R(1, 1) -> R(2, 1) -> U(2, 2) -> R(3, 2)。示例 2：
输入：command = "URR", obstacles = [[2, 2]], x = 3, y = 2
输出：false
解释：机器人在到达终点前会碰到(2, 2)的障碍物。示例 3：
输入：command = "URR", obstacles = [[4, 2]], x = 3, y = 2
输出：true
解释：到达终点后，再碰到障碍物也不影响返回结果。限制：
2 <= command的长度 <= 1000
command由U，R构成，且至少有一个U，至少有一个R
0 <= x <= 1e9, 0 <= y <= 1e9
0 <= obstacles的长度 <= 1000
obstacles[i]不为原点或者终点

---

class Solution {// 超时 代码
public:bool robot(string command, vector<vector<int>>& obstacles, int x, int y) {int ax = 0, by = 0;unordered_multimap<int,int> m;for(auto it = obstacles.begin(); it != obstacles.end(); it++){m.insert(make_pair((*it)[0],(*it)[1]));//建立哈希表}for(int i = 0; i < command.size(); i++){if(ax > x || by > y)break;//走过了，肯定达到不了终点if(command[i] == 'U')by += 1;elseax += 1;if(ax == x && by == y)return true;//达到终点if(i == command.size()-1)i = -1;//循环执行auto range = m.equal_range(ax);auto it = range.first;while(it != range.second)//查找当前坐标是否是障碍物{if(by == (*it).second)return false;++it;}   }return false;}
};

上面的效率还是有问题，可能不能这么干

---

正解：

• 找到一串命令可以走到的位置，存入哈希表
• 求出多少个循环可以到达终点，把终点移到上面一串指令走过的范围，进行检查
• 障碍物也是一样处理

class Solution {
public:bool robot(string command, vector<vector<int>>& obstacles, int x, int y) {int ax = 0, by = 0, circle, px, py;unordered_map<int,unordered_set<int>> m;m[0].insert(0);for(int i = 0; i < command.size(); i++){if(command[i] == 'U')by += 1;elseax += 1;m[ax].insert(by);//一串指令走过的点}circle = min(x/ax, y/by);//循环次数px = x-ax*circle;py = y-by*circle;if(!m.count(px) || !m[px].count(py))return false;//终点不在路径上for(int i = 0; i < obstacles.size(); ++i){if(obstacles[i][0] > x || obstacles[i][1] > y)continue;//障碍物在终点范围外circle = min(obstacles[i][0]/ax, obstacles[i][1]/by);px = obstacles[i][0]-ax*circle;py = obstacles[i][1]-by*circle;if(m.count(px) && m[px].count(py))return false;//路径包含障碍物}return true;}
};

12 ms 8.4 MB

2.4 覆盖 Hard

---

2.5 发 LeetCoin Hard