LeetCode 837. 新21点（动态规划）

文章目录

- 1. 题目
- 2. 解题
- - 2.1 暴力超时
  - 2.2 优化

1. 题目

爱丽丝参与一个大致基于纸牌游戏 “21点” 规则的游戏，描述如下：

爱丽丝以 0 分开始，并在她的得分少于 K 分时抽取数字。
抽取时，她从 [1, W] 的范围中随机获得一个整数作为分数进行累计，其中 W 是整数。
每次抽取都是独立的，其结果具有相同的概率。

当爱丽丝获得 >= K 分时，她就停止抽取数字。
爱丽丝的分数不超过 N 的概率是多少？

示例 1：
输入：N = 10, K = 1, W = 10
输出：1.00000
说明：爱丽丝得到一张卡，然后停止。示例 2：
输入：N = 6, K = 1, W = 10
输出：0.60000
说明：爱丽丝得到一张卡，然后停止。
在 W = 10 的 6 种可能下，她的得分不超过 N = 6 分。示例 3：
输入：N = 21, K = 17, W = 10
输出：0.73278提示：
0 <= K <= N <= 10000
1 <= W <= 10000
如果答案与正确答案的误差不超过 10^-5，则该答案将被视为正确答案通过。
此问题的判断限制时间已经减少。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/new-21-game
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

2.1 暴力超时

每个位置等于它前面w个位置以 1/w的该跳过来的概率值和
105 / 146 个通过测试用例

9811	# 超时
8890
7719

class Solution {
public:double new21Game(int N, int K, int W) {vector<double> dp(N+1, 0.0);dp[0] = 1.0;int i, wi;for(i = 0; i < K; ++i){for(wi = 1; wi <= W; ++wi){if(i+wi <= N)dp[i+wi] += dp[i]/W;}}double ans = 0.0;for(i = K; i <= N; ++i)ans += dp[i];return ans;}
};

2.2 优化

每个位置 i 之前的W个位置（相当于滑动窗口）的概率之和prob，到达 i 的的概率为 prob/W

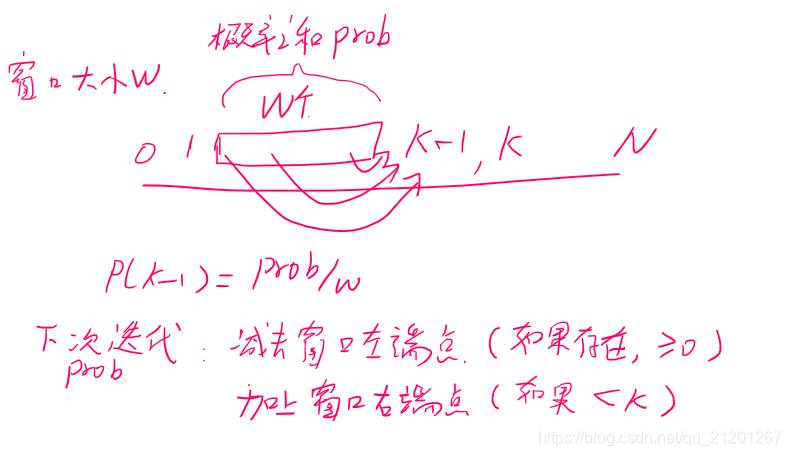
class Solution {
public:double new21Game(int N, int K, int W) {vector<double> dp(N+1, 0.0);if(K == 0 || N >= K + W) return 1.0;//肯定不会超出Ndp[0] = 1;double prob = 1.0;//停在 i前面 w个位置的概率之和， 初值在0位置概率为1int i;for(i = 1; i < K; ++i)//小于K时，可以继续，w个前缀可以加上本次的概率{if(i <= W){dp[i] = prob/W;//前面所有的位置都可以到此处，每个位置乘以1/wprob += dp[i];//前缀概率和，+本次}else	//超过w个了{dp[i] = (prob-dp[i-W-1])/W;//不在窗口内的，不能到i处了，需要减去prob += dp[i] - dp[i-W-1];//前缀+本次，-不在窗口内的}}for( ; i >= K && i <= N; ++i)// >= K 了， 不能再走了，不加本次的概率{if(i <= W)dp[i] = prob/W;else{dp[i] = (prob-dp[i-W-1])/W;prob -= dp[i-W-1];//不加本次的概率，在窗口w外的减去}}for(i = K, prob = 0.0; i <= N; ++i)prob += dp[i];return prob;}
};