目录

等宽离散

等频离散

聚类离散

附录：

rolling_mean函数解释

cut函数解释

其他数据预处理方法

---

一些数据挖掘算法中，特别是某些分类算法（eg:ID3算法、Aprioroi算法等），要求数据是分类属性形式。因此常常需要将连续属性变换成分类属性，即离散化。

离散化就是在数据的取值范围内设定若干个离散的花粉店，将取值范围划分为一些离散化的区间，最后用不同的符号护着整数值代表落在每个区间中的数据值。所以离散化涉及两个过程：确定分类数&将连续属性值映射到n个分类值。

常用的离散化方法：等宽离散、等频离散和聚类离散（一维）。

 

等宽离散

将属性的值域从最小值到最大值分成具有相同宽度的n个区间，n由数据特点决定，往往是需要有业务经验的人进行评估。

代码实现：

#-*- coding:utf-8 -*-
#数据离散化-等宽离散
import pandas as pddatafile = u'E:\\pythondata\\hk04.xlsx'
data = pd.read_excel(datafile)
data = data[u'回款金额'].copy()
k = 5 #设置离散之后的数据段为5#等宽离散
d1 = pd.cut(data,k,labels = range(k))#将回款金额等宽分成k类，命名为0,1,2,3,4,5，data经过cut之后生成了第一列为索引，第二列为当前行的回款金额被划分为0-5的哪一类，属于3这一类的第二列就显示为3def cluster_plot(d,k):import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = Falseplt.figure(figsize = (12,4))for j in range(0,k):plt.plot(data[d==j], [j for i in d[d==j]],'o')plt.ylim(-0.5, k-0.5)return pltcluster_plot(d1, k).show()

离散结果：

由这个离散结果我们可以直观的看出等宽离散的缺点，其缺点在于对噪点过于敏感，倾向于不均匀的把属性值分布到各个区间，导致有些区间的数值极多，而有些区间极少，严重损坏离散化之后建立的数据模型。

 

等频离散

将相同数量的记录放在每个区间，保证每个区间的数量基本一致。

代码实现：

#-*- coding:utf-8 -*-
#数据离散化-等频离散
import pandas as pddatafile = u'E:\\pythondata\\hk04.xlsx'
data = pd.read_excel(datafile)
data = data[u'回款金额'].copy()
k = 5 #设置离散之后的数据段为5#等频率离散化
w = [1.0*i/k for i in range(k+1)]
w = data.describe(percentiles = w)[4:4+k+1]
w[0] = w[0]*(1-1e-10)
d2 = pd.cut(data, w, labels = range(k))def cluster_plot(d,k):import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = Falseplt.figure(figsize = (12,4))for j in range(0,k):plt.plot(data[d==j], [j for i in d[d==j]],'o')plt.ylim(-0.5, k-0.5)return pltcluster_plot(d2, k).show()

离散结果：

由离散结果看出，等频离散不会像等宽离散一样，出现某些区间极多或者极少的情况。但是根据等频离散的原理，为了保证每个区间的数据一致，很有可能将原本是相同的两个数值却被分进了不同的区间，这对最终模型的损坏程度一点都不亚于等宽离散。

 

聚类离散

一维聚类离散包括两个过程：通过聚类算法（K-Means算法）将连续属性值进行聚类，处理聚类之后的到的k个簇，得到每个簇对应的分类值（类似这个簇的标记）。

代码实现：

#-*- coding:utf-8 -*-
#数据离散化-聚类离散
import pandas as pddatafile = u'E:\\pythondata\\hk04.xlsx'
data = pd.read_excel(datafile)
data = data[u'回款金额'].copy()
k = 5 #设置离散之后的数据段为5#聚类离散
from sklearn.cluster import KMeanskmodel = KMeans(n_clusters = k, n_jobs = 4)#n_jobs是并行数，一般等于CPU数
kmodel.fit(data.reshape((len(data), 1)))
c = pd.DataFrame(kmodel.cluster_centers_, columns=list('a')).sort_values(by='a')
#rolling_mean表示移动平均，即用当前值和前2个数值取平均数，
#由于通过移动平均，会使得第一个数变为空值，因此需要使用.iloc[1:]过滤掉空值。
w = pd.rolling_mean(c, 2).iloc[1:]#此处w=[2174.1003996693553, 8547.46386803177, 22710.538501243103, 48516.861774600904]
w = [0] + list(w[0]) + [data.max()]#把首末边界点加上，首边界为0，末边界为data的最大值120000，此处w=[0, 2174.1003996693553, 8547.46386803177, 22710.538501243103, 48516.861774600904, 120000.0]
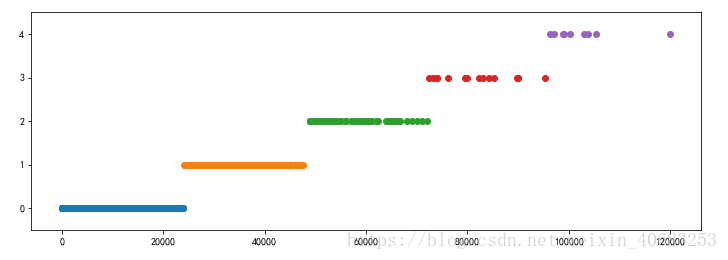
d3 = pd.cut(data, w, labels = range(k))#cut函数实现将data中的数据按照w的边界分类。def cluster_plot(d,k):import matplotlib.pyplot as pltplt.rcParams['font.sans-serif'] = ['SimHei']plt.rcParams['axes.unicode_minus'] = Falseplt.figure(figsize = (12,4))for j in range(0,k):plt.plot(data[d==j], [j for i in d[d==j]],'o')plt.ylim(-0.5, k-0.5)return pltcluster_plot(d3, k).show()

离散结果：

三种离散化方法中，最得本宫心意的便是最后这个聚类离散，但是即便是这般如花似玉，也有她的弊端：无法自己学习得知离散后簇的个数，依然需要内阁大学士来决定。

 

附录：

rolling_mean函数解释

pandas.rolling_mean(arg, window, min_periods=None, freq=None, center=False, how=None, **kwargs)

rolling_mean函数表示通过移动窗口求平均值，即用当前值和前[window]个数值取平均数，得到新的数值。

import pandas as pddata = [3, 60, 83, 100, 52, 36]#源数据
data = pd.DataFrame(data).sort_values(0)  
w2 = pd.rolling_mean(data, 2)#设置移动窗口为2，即用当前值和前2个数值取平均数
w3 = pd.rolling_mean(data, 3)#用当前值和前3个数值取平均数
print("源数据:\n", data)
print("移动窗口数为2:\n", w2)
print("移动窗口数为3:\n", w3)

运行结果：

源数据:0
0    3
5   36
4   52
1   60
2   83
3  100
移动窗口数为2:0
0   NaN
5  19.5
4  44.0
1  56.0
2  71.5
3  91.5
移动窗口数为3:0
0        NaN
5        NaN
4  30.333333
1  49.333333
2  65.000000
3  81.000000

rolling的一系列函数中，除了rolling_mean（移动窗口的均值），还有rolling_median（移动窗口的中位数）、rolling_var （移动窗口的方差）、rolling_std （移动窗口的标准差）、rolling_cov （移动窗口的协方差）、rolling_sum （移动窗口的和）、rolling_min （移动窗口的最小值）、rolling_max （移动窗口的最大值）、rolling_corr （移动窗口的相关系数）、rolling_count （计算各个窗口中非NA观测值的数量）。最常用的还是rolling_mean了，作用类似时间序列中提到的移动平滑。

 

cut函数解释

cut()函数可以将一个数组中的数据切分成几个部分。两种用法：可以设置分类的边界，也可以仅规定分类后的个数。 cut([被分割的数据]，[将数据分为几个部分])

import pandas as pddata = [3, 60, 83, 100, 52, 36]#源数据
w = [0, 25, 50, 75, 100]#规定了分类的边界
v = 4 #仅规定分类的个数，不规定边界值
data_cut1 = pd.cut(data, w)
data_cut2 = pd.cut(data, v)
print("规定了分类的边界:\n", data_cut1)
print("\n规定了分类的个数:\n", data_cut2)

运行结果：

规定了分类的边界:[(0, 25], (50, 75], (75, 100], (75, 100], (50, 75], (25, 50]]
Categories (4, interval[int64]): [(0, 25] < (25, 50] < (50, 75] < (75, 100]]规定了分类的个数:[(2.903, 27.25], (51.5, 75.75], (75.75, 100.0], (75.75, 100.0], (51.5, 75.75], (27.25, 51.5]]
Categories (4, interval[float64]): [(2.903, 27.25] < (27.25, 51.5] < (51.5, 75.75] < (75.75, 100.0]]

 

其他数据预处理方法

拉格朗日插值法补充缺失值

清洗重复数据

数据预处理 - 归一化与标准化