算法简介

决策数(Decision Tree)在机器学习中也是比较常见的一种算法，属于监督学习中的一种。其中ID3算法是以信息熵和信息增益作为衡量标准的分类算法。

信息熵(Entropy)

熵的概念主要是指信息的混乱程度，变量的不确定性越大，熵的值也就越大，熵的公式可以表示为：

信息增益(Information gain) - ID3算法

信息增益指的是根据特征划分数据前后熵的变化，可以用下面的公式表示：

根据不同特征分类后熵的变化不同，信息增益也不同，信息增益越大，区分样本的能力越强，越具有代表性。这是一种自顶向下的贪心策略，即在ID3中根据“最大信息增益”原则选择特征。

ID3采用信息增益来选择特征，存在一个缺点，它一般会优先选择有较多属性值的特征，因为属性值多的特征会有相对较大的信息增益。(这是因为：信息增益反映的给定一个条件以后不确定性减少的程度,必然是分得越细的数据集确定性更高,也就是条件熵越小,信息增益越大)。

信息增益率(gain ratio) - C4.5算法

为了避免ID3的不足，C4.5中是用信息增益率(gain ratio)来作为选择分支的准则。对于有较多属性值的特征，信息增益率的分母Split information（S,A），我们称之为分裂信息，会稀释掉它对特征选择的影响。分裂信息（公式1）和信息增益率（公式2）的计算如下所示。

源数据

收入	身高	长相	体型	是否见面
一般	高	丑	胖	否
高	一般	帅	瘦	是
一般	一般	一般	一般	否
高	高	丑	一般	是
一般	高	帅	胖	是

这是一位单身女性根据对方的一些基本条件，判断是否去约会的数据，此处展示前五行。我们要通过这位女士历史的数据建立决策树模型，使得尽量给这位女性推送她比较愿意约会的异性信息。

代码实现 - ID3算法

from math import log
import operator
import numpy as np
import pandas as pd
from pandas import DataFrame,Series# 计算数据的熵(entropy)-原始熵
def dataentropy(data, feat):  lendata=len(data)  # 数据条数labelCounts={} # 数据中不同类别的条数for featVec in data:category=featVec[-1] # 每行数据的最后一个字（叶子节点）if category not in labelCounts.keys():labelCounts[category]=0 labelCounts[category]+=1  # 统计有多少个类以及每个类的数量entropy=0for key in labelCounts:prob=float(labelCounts[key])/lendata # 计算单个类的熵值entropy-=prob*log(prob,2) # 累加每个类的熵值return entropy# 处理后导入数据数据
def Importdata(datafile): dataa = pd.read_excel(datafile)#datafile是excel文件，所以用read_excel,如果是csv文件则用read_csv#将文本中不可直接使用的文本变量替换成数字productDict={'高':1,'一般':2,'低':3, '帅':1,  '丑':3,  '胖':3,  '瘦':1,  '是':1,  '否':0}dataa['income'] = dataa['收入'].map(productDict)#将每一列中的数据按照字典规定的转化成数字dataa['hight'] = dataa['身高'].map(productDict)dataa['look'] = dataa['长相'].map(productDict)dataa['shape'] = dataa['体型'].map(productDict)dataa['is_meet'] = dataa['是否见面'].map(productDict)data = dataa.iloc[:,5:].values.tolist()#取量化后的几列，去掉文本列b = dataa.iloc[0:0,5:-1]labels = b.columns.values.tolist()#将标题中的值存入列表中return data,labels# 按某个特征value分类后的数据
def splitData(data,i,value): splitData=[]for featVec in data:if featVec[i]==value:rfv =featVec[:i]rfv.extend(featVec[i+1:])splitData.append(rfv)return splitData# 选择最优的分类特征
def BestSplit(data):  numFea = len(data[0])-1#计算一共有多少个特征，因为最后一列一般是分类结果，所以需要-1baseEnt = dataentropy(data,-1)   # 定义初始的熵,用于对比分类后信息增益的变化bestInfo = 0bestFeat = -1for i in range(numFea):featList = [rowdata[i] for rowdata in data]uniqueVals = set(featList)newEnt = 0for value in uniqueVals:subData = splitData(data,i,value)#获取按照特征value分类后的数据prob =len(subData)/float(len(data))newEnt +=prob*dataentropy(subData,i)  # 按特征分类后计算得到的熵info = baseEnt - newEnt  # 原始熵与按特征分类后的熵的差值，即信息增益if (info>bestInfo):   # 若按某特征划分后，若infoGain大于bestInf，则infoGain对应的特征分类区分样本的能力更强，更具有代表性。 bestInfo=info #将infoGain赋值给bestInf，如果出现比infoGain更大的信息增益，说明还有更好地特征分类bestFeat = i #将最大的信息增益对应的特征下标赋给bestFea，返回最佳分类特征return bestFeat #按分类后类别数量排序，取数量较大的
def majorityCnt(classList):    c_count={}for i in classList:if i not in c_count.keys():c_count[i]=0c_count[i]+=1ClassCount = sorted(c_count.items(),key=operator.itemgetter(1),reverse=True)#按照统计量降序排序return ClassCount[0][0]#reverse=True表示降序，因此取[0][0]，即最大值#建树
def createTree(data,labels):classList = [rowdata[-1] for rowdata in data]  # 取每一行的最后一列，分类结果（1/0）if classList.count(classList[0])==len(classList):return classList[0]if len(data[0])==1:return majorityCnt(classList)bestFeat = BestSplit(data) #根据信息增益选择最优特征bestLab = labels[bestFeat]myTree = {bestLab:{}} #分类结果以字典形式保存del(labels[bestFeat])featValues = [rowdata[bestFeat] for rowdata in data]uniqueVals = set(featValues)for value in uniqueVals:subLabels = labels[:]myTree[bestLab][value] = createTree(splitData(data,bestFeat,value),subLabels)return myTreeif __name__=='__main__':datafile = u'E:\\pythondata\\tree.xlsx'#文件所在位置，u为防止路径中有中文名称data, labels=Importdata(datafile)  # 导入数据print(createTree(data, labels))  # 输出决策树模型结果

运行结果：

{'hight': {1: {'look': {1: {'income': {1: {'shape': {1: 1, 2: 1}}, 2: 1, 3: {'shape': {1: 1, 2: 0}}}}, 2: 1, 3: {'income': {1: 1, 2: 0}}}}, 2: {'income': {1: 1, 2: {'look': {1: 1, 2: 0}}, 3: 0}}, 3: {'look': {1: {'shape': {3: 0, 1: 1}}, 2: 0, 3: 0}}}}

对应的决策树：

代码实现 - C4.5算法

C4.5算法和ID3算法逻辑很相似，只是ID3算法是用信息增益来选择特征，而C4.5算法是用的信息增益率，因此对代码的影响也只有BestSplit(data)函数的定义部分，只需要加一个信息增益率的计算即可，BestSplit(data)函数定义代码更改后如下：

# 选择最优的分类特征
def BestSplit(data):  numFea = len(data[0])-1#计算一共有多少个特征，因为最后一列一般是分类结果，所以需要-1baseEnt = dataentropy(data,-1)   # 定义初始的熵,用于对比分类后信息增益的变化bestGainRate = 0bestFeat = -1for i in range(numFea):featList = [rowdata[i] for rowdata in data]uniqueVals = set(featList)newEnt = 0for value in uniqueVals:subData = splitData(data,i,value)#获取按照特征value分类后的数据prob =len(subData)/float(len(data))newEnt +=prob*dataentropy(subData,i)  # 按特征分类后计算得到的熵info = baseEnt - newEnt  # 原始熵与按特征分类后的熵的差值，即信息增益splitonfo = dataentropy(subData,i) #分裂信息if splitonfo == 0:#若特征值相同（eg:长相这一特征的值都是帅），即splitonfo和info均为0，则跳过该特征continueGainRate = info/splitonfo #计算信息增益率if (GainRate>bestGainRate):   # 若按某特征划分后，若infoGain大于bestInf，则infoGain对应的特征分类区分样本的能力更强，更具有代表性。 bestGainRate=GainRate #将infoGain赋值给bestInf，如果出现比infoGain更大的信息增益，说明还有更好地特征分类bestFeat = i #将最大的信息增益对应的特征下标赋给bestFea，返回最佳分类特征return bestFeat

运行结果：

{'hight': {1: {'look': {1: {'income': {1: {'shape': {0: 0, 1: 1}}, 2: 1, 3: {'shape': {0: 0, 1: 1}}}}, 2: 1, 3: {'shape': {0: 0, 1: 1}}}}, 2: {'shape': {0: 0, 1: 1}}, 3: {'shape': {1: 0, 3: {'look': {0: 0, 1: 1}}}}}}

画决策树代码-treePlotter

决策树可以代码实现的，不需要按照运行结果一点一点手动画图。

import treePlotter
treePlotter.createPlot(myTree)

其中treePlotter模块是如下一段代码，可以保存为.py文件，放在Python/Lib/site-package目录下，然后用的时候import 【文件名】就可以了。

treePlotter模块代码：

#绘制决策树
import matplotlib.pyplot as plt# 定义文本框和箭头格式，boxstyle用于指定边框类型，color表示填充色
decisionNode = dict(boxstyle="round4", color='#ccccff')  #定义判断结点为圆角长方形，填充浅蓝色
leafNode = dict(boxstyle="circle", color='#66ff99')  #定义叶结点为圆形，填充绿色
arrow_args = dict(arrowstyle="<-", color='ffcc00')  #定义箭头及颜色#绘制带箭头的注释
def plotNode(nodeTxt, centerPt, parentPt, nodeType):createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',xytext=centerPt, textcoords='axes fraction',va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)#计算叶结点数
def getNumLeafs(myTree):numLeafs = 0firstStr = myTree.keys()[0]secondDict = myTree[firstStr]for key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict':numLeafs += getNumLeafs(secondDict[key])else:numLeafs += 1return numLeafs#计算树的层数
def getTreeDepth(myTree):maxDepth = 0firstStr = myTree.keys()[0]secondDict = myTree[firstStr]for key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict':thisDepth = 1 + getTreeDepth(secondDict[key])else:thisDepth = 1if thisDepth > maxDepth:maxDepth = thisDepthreturn maxDepth#在父子结点间填充文本信息
def plotMidText(cntrPt, parentPt, txtString):xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]createPlot.ax1.text(xMid, yMid, txtString, va="center", ha="center", rotation=30)def plotTree(myTree, parentPt, nodeTxt):numLeafs = getNumLeafs(myTree)depth = getTreeDepth(myTree)firstStr = myTree.keys()[0]cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)plotMidText(cntrPt, parentPt, nodeTxt)  #在父子结点间填充文本信息plotNode(firstStr, cntrPt, parentPt, decisionNode)  #绘制带箭头的注释secondDict = myTree[firstStr]plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalDfor key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict':plotTree(secondDict[key], cntrPt, str(key))else:plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalWplotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalDdef createPlot(inTree):fig = plt.figure(1, facecolor='white')fig.clf()axprops = dict(xticks=[], yticks=[])createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)plotTree.totalW = float(getNumLeafs(inTree))plotTree.totalD = float(getTreeDepth(inTree))plotTree.xOff = -0.5 / plotTree.totalW;plotTree.yOff = 1.0;plotTree(inTree, (0.5, 1.0), '')plt.show()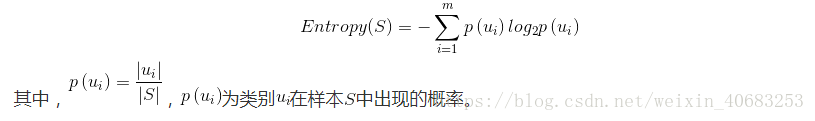