LeetCode 1444. 切披萨的方案数（DP）

1. 题目

给你一个 rows x cols 大小的矩形披萨和一个整数 k ，矩形包含两种字符： ‘A’ （表示苹果）和 ‘.’ （表示空白格子）。
你需要切披萨 k-1 次，得到 k 块披萨并送给别人。

切披萨的每一刀，先要选择是向垂直还是水平方向切，再在矩形的边界上选一个切的位置，将披萨一分为二。
如果垂直地切披萨，那么需要把左边的部分送给一个人，如果水平地切，那么需要把上面的部分送给一个人。
在切完最后一刀后，需要把剩下来的一块送给最后一个人。

请你返回确保每一块披萨包含至少一个苹果的切披萨方案数。
由于答案可能是个很大的数字，请你返回它对 10^9 + 7 取余的结果。

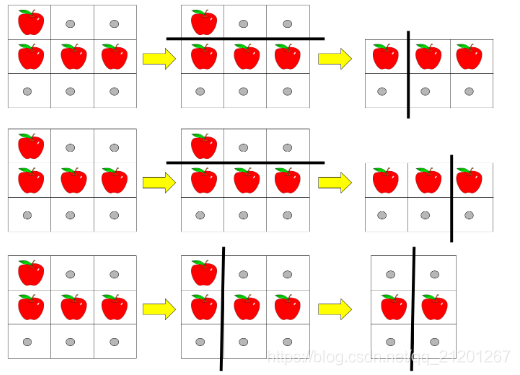
在这里插入图片描述

示例 1：
输入：pizza = ["A..","AAA","..."], k = 3
输出：3 
解释：上图展示了三种切披萨的方案。注意每一块披萨都至少包含一个苹果。示例 2：
输入：pizza = ["A..","AA.","..."], k = 3
输出：1示例 3：
输入：pizza = ["A..","A..","..."], k = 1
输出：1提示：
1 <= rows, cols <= 50
rows == pizza.length
cols == pizza[i].length
1 <= k <= 10
pizza 只包含字符 'A' 和 '.' 。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-ways-of-cutting-a-pizza
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

先用dp方法求出以（i,j）位置为右下角，左上角为（0,0）的区域的苹果数量
建立3维数组，dp[i][j][k]表示切完k次后，剩余蛋糕左上角在i, j位置时的方案数
初始化，dp[0][0][0] = 1
样本维度为切的次数 k
状态维度，这次切之前的状态（蛋糕左上角位置 i, j）
状态转移，这次切完后蛋糕左上角位置（横向切，ni，j；竖向切，i, nj，切的次数 +1）
转移条件：切出去的蛋糕当中有苹果（用上面求得的苹果数量，dp公式求得）
最后求结果总和：最后的一块蛋糕中有苹果，sum += dp[i][j][k-1]

class Solution {
public:int ways(vector<string>& pizza, int k) {int m = pizza.size(), n = pizza[0].size(), i, j, sum = 0;vector<vector<int>> app(m,vector<int>(n,0));for(i = 0; i < n; ++i){if(pizza[0][i]=='A')sum++;app[0][i] = sum;}sum = 0;for(i = 0; i < m; ++i){if(pizza[i][0]=='A')sum++;app[i][0] = sum;}for(i = 1; i < m; ++i){for(j = 1; j < n; ++j){app[i][j] = (pizza[i][j]=='A'? 1 : 0) +app[i-1][j]+app[i][j-1]-app[i-1][j-1];}}//求得以i,j为左下角的矩形中的苹果数量vector<vector<vector<int>>> dp(m,vector<vector<int>>(n,vector<int>(k,0)));//dp[i][j][k]表示切完k次后，剩余蛋糕左上角 在i,j位置时的方案数dp[0][0][0] = 1;int ni, nj, appcount;//下一个转移状态的位置for(int cut = 1; cut < k; ++cut)for(i = 0; i < m; ++i){for(j = 0; j < n; ++j){if(dp[i][j][cut-1] != 0)//上一次cut完后，剩余蛋糕左上角在i,j{for(ni = i+1; ni < m; ++ni){	//横向切，切完后的剩余左上角为 ni, jappcount = app[ni-1][n-1]-(j>0 ? app[ni-1][j-1]:0)-(i>0?app[i-1][n-1]:0)+(i>0&&j>0 ? app[i-1][j-1] : 0);if(appcount != 0)dp[ni][j][cut] = (dp[ni][j][cut]+dp[i][j][cut-1])%1000000007;}for(nj = j+1; nj < n; ++nj){	//竖向切appcount = app[m-1][nj-1]-(i>0?app[i-1][nj-1]:0)-(j>0?app[m-1][j-1]:0)+(i>0&&j>0 ? app[i-1][j-1] : 0);if(appcount != 0)dp[i][nj][cut] = (dp[i][nj][cut]+dp[i][j][cut-1])%1000000007;}}}}sum = 0;for(i = 0; i < m; ++i)for(j = 0; j < n; ++j){appcount = app[m-1][n-1]-(j>0?app[m-1][j-1]:0)-(i>0?app[i-1][n-1]:0)+(i>0&&j>0 ? app[i-1][j-1]:0);if(appcount != 0)sum = (sum+dp[i][j][k-1])%1000000007;}return sum;}
};