LeetCode 723. 粉碎糖果（模拟）

文章目录

- 1. 题目
- 2. 解题

1. 题目

这个问题是实现一个简单的消除算法。

给定一个二维整数数组 board 代表糖果所在的方格，不同的正整数 board[i][j] 代表不同种类的糖果，如果 board[i][j] = 0 代表 (i, j) 这个位置是空的。
给定的方格是玩家移动后的游戏状态，现在需要你根据以下规则粉碎糖果，使得整个方格处于稳定状态并最终输出。

如果有三个及以上水平或者垂直相连的同种糖果，同一时间将它们粉碎，即将这些位置变成空的。
在同时粉碎掉这些糖果之后，如果有一个空的位置上方还有糖果，那么上方的糖果就会下落直到碰到下方的糖果或者底部，这些糖果都是同时下落，也不会有新的糖果从顶部出现并落下来。
通过前两步的操作，可能又会出现可以粉碎的糖果，请继续重复前面的操作。
当不存在可以粉碎的糖果，也就是状态稳定之后，请输出最终的状态。
你需要模拟上述规则并使整个方格达到稳定状态，并输出。

样例 :
输入:
board = 
[[110,5,112,113,114],
[210,211,5,213,214],
[310,311,3,313,314],
[410,411,412,5,414],
[5,1,512,3,3],
[610,4,1,613,614],
[710,1,2,713,714],
[810,1,2,1,1],
[1,1,2,2,2],
[4,1,4,4,1014]]
输出:
[[0,0,0,0,0],[0,0,0,0,0],[0,0,0,0,0],
[110,0,0,0,114],[210,0,0,0,214],
[310,0,0,113,314],[410,0,0,213,414],
[610,211,112,313,614],[710,311,412,613,714],
[810,411,512,713,1014]]

解释:
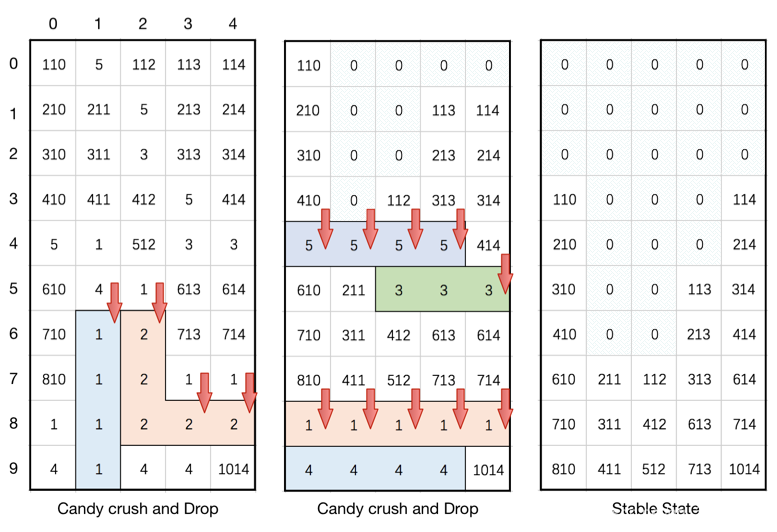
在这里插入图片描述

注释 :
board 数组的行数区间是 [3, 50]。
board[i] 数组的长度区间（即 board 数组的列数区间）是 [3, 50]。
每个 board[i][j] 初始整数范围是 [1, 2000]。

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/candy-crush
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

把连续三个不为0的标记为负数，待删除，横向和纵向都要扫描
把标记为负数的置为0
按纵向扫描，填补下方的空白，双指针法
递归处理，如果没有需要操作的，达到稳态，返回不再递归

class Solution {
public:vector<vector<int>> candyCrush(vector<vector<int>>& b) {bool todo = false;int m = b.size(), n = b[0].size(), i, j, up, down;for(i = 0; i < m; ++i)//横向检查for(j = 0; j < n-2; ++j){if(b[i][j] == 0)continue;if(abs(b[i][j])==abs(b[i][j+1]) && abs(b[i][j+1])==abs(b[i][j+2])){b[i][j] = b[i][j+1] = b[i][j+2] = -abs(b[i][j]);//标记为负的todo = true;}}for(j = 0; j < n; ++j)//纵向检查for(i = 0; i < m-2; ++i){if(b[i][j] == 0)continue;if(abs(b[i][j])==abs(b[i+1][j]) && abs(b[i+1][j])==abs(b[i+2][j])){b[i][j] = b[i+1][j] = b[i+2][j] = -abs(b[i][j]);//标记为负的todo = true;}}for(i = 0; i < m; ++i)//负的 标记为0要删除for(j = 0; j < n; ++j)if(b[i][j] < 0)b[i][j] = 0;for(j = 0; j < n; ++j)//纵向掉落{down = up = m-1;//从最底下开始往上找while(down >= 0){	//双指针搬移数据if(b[down][j] == 0)//底下待填{up = min(down, up);//up记住上次的位置while(up >= 0 && b[up][j] == 0)up--;if(up >= 0)//上面找到糖果swap(b[down][j], b[up][j]);//交换elsebreak;//找完了}down--;}}if(todo)candyCrush(b);return b;}
};