测试题：参考博文

笔记：02.改善深层神经网络：超参数调试、正则化以及优化 W2.优化算法

• 导入一些包

import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasetsfrom opt_utils import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from testCases import *%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

1. 梯度下降

（Batch）Gradient Descent 梯度下降 对每一层都进行：

$W^{[l]}=W^{[l]}-\alpha \ast d{W}^{[l]}$

$b^{[l]}=b^{[l]}-\alpha \ast d{b}^{[l]}$

$l$ 是层号，$\alpha$ 是学习率

# GRADED FUNCTION: update_parameters_with_gddef update_parameters_with_gd(parameters, grads, learning_rate):"""Update parameters using one step of gradient descentArguments:parameters -- python dictionary containing your parameters to be updated:parameters['W' + str(l)] = Wlparameters['b' + str(l)] = blgrads -- python dictionary containing your gradients to update each parameters:grads['dW' + str(l)] = dWlgrads['db' + str(l)] = dbllearning_rate -- the learning rate, scalar.Returns:parameters -- python dictionary containing your updated parameters """L = len(parameters) // 2 # number of layers in the neural networks# Update rule for each parameterfor l in range(L):### START CODE HERE ### (approx. 2 lines)parameters["W" + str(l+1)] = parameters['W'+str(l+1)] - learning_rate * grads['dW'+str(l+1)]parameters["b" + str(l+1)] = parameters['b'+str(l+1)] - learning_rate * grads['db'+str(l+1)]### END CODE HERE ###return parameters

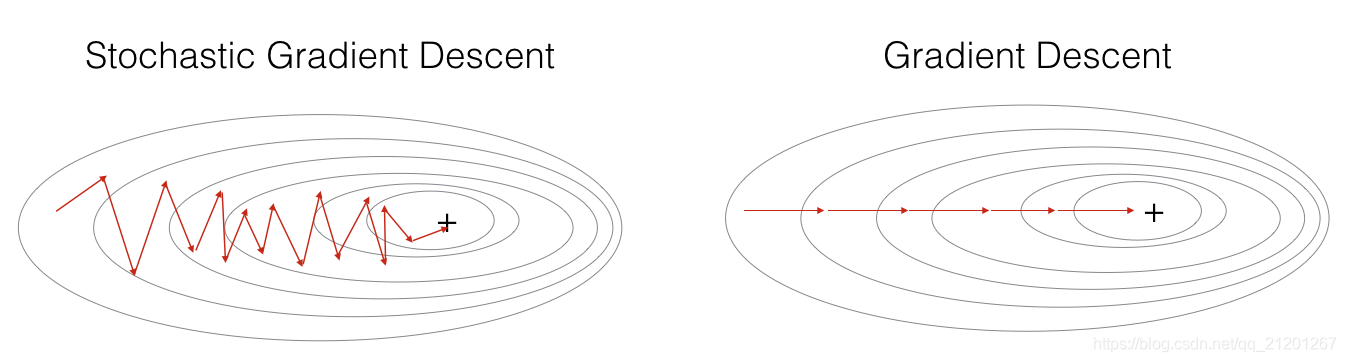
Stochastic Gradient Descent 随机梯度下降

• 每次只用1个样本来更新梯度，当训练集很大的时候，SGD 很快
• 其寻优过程有震荡
  

代码差异：

• (Batch) Gradient Descent:

X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):# Forward propagationa, caches = forward_propagation(X, parameters)# Compute cost.cost = compute_cost(a, Y)# Backward propagation.grads = backward_propagation(a, caches, parameters)# Update parameters.parameters = update_parameters(parameters, grads)

• Stochastic Gradient Descent:

X = data_input
Y = labels
parameters = initialize_parameters(layers_dims)
for i in range(0, num_iterations):for j in range(0, m):# Forward propagationa, caches = forward_propagation(X[:,j], parameters)# Compute costcost = compute_cost(a, Y[:,j])# Backward propagationgrads = backward_propagation(a, caches, parameters)# Update parameters.parameters = update_parameters(parameters, grads)

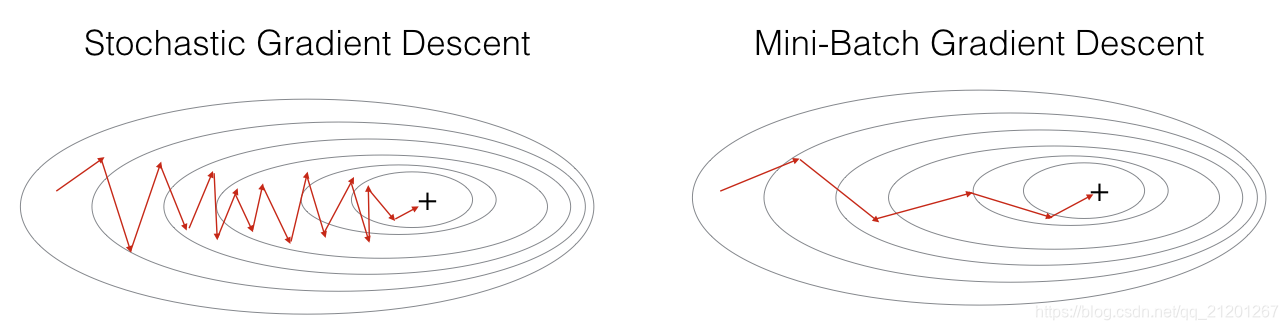
3者的差别在于，一次梯度更新时，用到的样本数量不同

调好参数的 mini-batch 梯度下降，通常优于梯度下降或随机梯度下降（特别是当训练集很大时）

2. mini-Batch 梯度下降

如何从训练集 $(X,Y)$ 建立 mini-batches

步骤1：随机打乱数据，X 和 Y 是同步进行的，保持对应关系

步骤2：切分数据集（每个子集大小为 mini_batch_size，最后一个可能不够，没关系）

# GRADED FUNCTION: random_mini_batchesdef random_mini_batches(X, Y, mini_batch_size = 64, seed = 0):"""Creates a list of random minibatches from (X, Y)Arguments:X -- input data, of shape (input size, number of examples)Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)mini_batch_size -- size of the mini-batches, integerReturns:mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)"""np.random.seed(seed)            # To make your "random" minibatches the same as oursm = X.shape[1]                  # number of training examplesmini_batches = []# Step 1: Shuffle (X, Y)permutation = list(np.random.permutation(m))shuffled_X = X[:, permutation]shuffled_Y = Y[:, permutation].reshape((1,m))# Step 2: Partition (shuffled_X, shuffled_Y). Minus the end case.num_complete_minibatches = math.floor(m/mini_batch_size) # number of mini batches of size mini_batch_size in your partitionningfor k in range(0, num_complete_minibatches):### START CODE HERE ### (approx. 2 lines)mini_batch_X = X[:, k*mini_batch_size : (k+1)*mini_batch_size]mini_batch_Y = Y[:, k*mini_batch_size : (k+1)*mini_batch_size]### END CODE HERE ###mini_batch = (mini_batch_X, mini_batch_Y)mini_batches.append(mini_batch)# Handling the end case (last mini-batch < mini_batch_size)if m % mini_batch_size != 0:### START CODE HERE ### (approx. 2 lines)mini_batch_X = X[:, num_complete_minibatches*mini_batch_size : ]mini_batch_Y = Y[:, num_complete_minibatches*mini_batch_size : ]### END CODE HERE ###mini_batch = (mini_batch_X, mini_batch_Y)mini_batches.append(mini_batch)return mini_batches

3. 动量

带动量 的 梯度下降可以降低 mini-batch 梯度下降时的震荡

原因：Momentum 考虑过去的梯度对当前的梯度进行平滑，梯度不会剧烈变化

• 初始化梯度的 初速度为 0

# GRADED FUNCTION: initialize_velocitydef initialize_velocity(parameters):"""Initializes the velocity as a python dictionary with:- keys: "dW1", "db1", ..., "dWL", "dbL" - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.Arguments:parameters -- python dictionary containing your parameters.parameters['W' + str(l)] = Wlparameters['b' + str(l)] = blReturns:v -- python dictionary containing the current velocity.v['dW' + str(l)] = velocity of dWlv['db' + str(l)] = velocity of dbl"""L = len(parameters) // 2 # number of layers in the neural networksv = {}# Initialize velocityfor l in range(L):### START CODE HERE ### (approx. 2 lines)v["dW" + str(l+1)] = np.zeros(parameters['W'+str(l+1)].shape)v["db" + str(l+1)] = np.zeros(parameters['b'+str(l+1)].shape)### END CODE HERE ###return v

• 对每一层，更新动量
  $$\{\begin{array}{l}{v}_{d{W}^{[l]}}=\beta v_{d{W}^{[l]}}+(1-\beta )d{W}^{[l]}\\ W^{[l]}=W^{[l]}-\alpha v_{d{W}^{[l]}}\end{array}$$

$$\{\begin{array}{l}{v}_{d{b}^{[l]}}=\beta v_{d{b}^{[l]}}+(1-\beta )d{b}^{[l]}\\ b^{[l]}=b^{[l]}-\alpha v_{d{b}^{[l]}}\end{array}$$

# GRADED FUNCTION: update_parameters_with_momentumdef update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):"""Update parameters using MomentumArguments:parameters -- python dictionary containing your parameters:parameters['W' + str(l)] = Wlparameters['b' + str(l)] = blgrads -- python dictionary containing your gradients for each parameters:grads['dW' + str(l)] = dWlgrads['db' + str(l)] = dblv -- python dictionary containing the current velocity:v['dW' + str(l)] = ...v['db' + str(l)] = ...beta -- the momentum hyperparameter, scalarlearning_rate -- the learning rate, scalarReturns:parameters -- python dictionary containing your updated parameters v -- python dictionary containing your updated velocities"""L = len(parameters) // 2 # number of layers in the neural networks# Momentum update for each parameterfor l in range(L):### START CODE HERE ### (approx. 4 lines)# compute velocitiesv["dW" + str(l+1)] = beta* v["dW" + str(l+1)] + (1-beta)*grads['dW' + str(l+1)]v["db" + str(l+1)] = beta* v["db" + str(l+1)] + (1-beta)*grads['db' + str(l+1)]# update parametersparameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*v["dW" + str(l+1)]parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*v["db" + str(l+1)]### END CODE HERE ###return parameters, v

注意：

• 速度 v 初始化为 0，算法需要几次迭代后才能把 v 加上来，然后开始采用大的步长
• $\beta =0$ 就是不带动量的标准梯度下降

如何选择 $\beta$：

• $\beta$ 越大，考虑的过去的梯度越多，梯度输出也更光滑，太大也不行，过度光滑
• 经常取值为 0.8 - 0.999 之间，如果不确定，0.9 是个合理的默认值
• 参数验证选取，看其如何影响损失函数

4. Adam

参看笔记

对每一层：
$$\{\begin{array}{l}{v}_{d{W}^{[l]}}={\beta }_1{v}_{d{W}^{[l]}}+(1-{\beta }_1)\frac{\partial \mathcal{J}}{\partial W^{[l]}}\\ v_{d{W}^{[l]}}^{corrected}=\frac{v_{d{W}^{[l]}}}{1-({\beta }_1{)}^t}\\ s_{d{W}^{[l]}}={\beta }_2{s}_{d{W}^{[l]}}+(1-{\beta }_2)(\frac{\partial \mathcal{J}}{\partial W^{[l]}}{)}^2\\ s_{d{W}^{[l]}}^{corrected}=\frac{s_{d{W}^{[l]}}}{1-({\beta }_2{)}^t}\\ W^{[l]}=W^{[l]}-\alpha \frac{v_{d{W}^{[l]}}^{corrected}}{\sqrt{s_{d{W}^{[l]}}^{corrected}}+\epsilon }\end{array}$$

• 初始化为 0

# GRADED FUNCTION: initialize_adamdef initialize_adam(parameters) :"""Initializes v and s as two python dictionaries with:- keys: "dW1", "db1", ..., "dWL", "dbL" - values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.Arguments:parameters -- python dictionary containing your parameters.parameters["W" + str(l)] = Wlparameters["b" + str(l)] = blReturns: v -- python dictionary that will contain the exponentially weighted average of the gradient.v["dW" + str(l)] = ...v["db" + str(l)] = ...s -- python dictionary that will contain the exponentially weighted average of the squared gradient.s["dW" + str(l)] = ...s["db" + str(l)] = ..."""L = len(parameters) // 2 # number of layers in the neural networksv = {}s = {}# Initialize v, s. Input: "parameters". Outputs: "v, s".for l in range(L):### START CODE HERE ### (approx. 4 lines)v["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)v["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)s["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)s["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)### END CODE HERE ###return v, s

• 迭代更新

# GRADED FUNCTION: update_parameters_with_adamdef update_parameters_with_adam(parameters, grads, v, s, t, learning_rate = 0.01,beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8):"""Update parameters using AdamArguments:parameters -- python dictionary containing your parameters:parameters['W' + str(l)] = Wlparameters['b' + str(l)] = blgrads -- python dictionary containing your gradients for each parameters:grads['dW' + str(l)] = dWlgrads['db' + str(l)] = dblv -- Adam variable, moving average of the first gradient, python dictionarys -- Adam variable, moving average of the squared gradient, python dictionarylearning_rate -- the learning rate, scalar.beta1 -- Exponential decay hyperparameter for the first moment estimates beta2 -- Exponential decay hyperparameter for the second moment estimates epsilon -- hyperparameter preventing division by zero in Adam updatesReturns:parameters -- python dictionary containing your updated parameters v -- Adam variable, moving average of the first gradient, python dictionarys -- Adam variable, moving average of the squared gradient, python dictionary"""L = len(parameters) // 2                 # number of layers in the neural networksv_corrected = {}                         # Initializing first moment estimate, python dictionarys_corrected = {}                         # Initializing second moment estimate, python dictionary# Perform Adam update on all parametersfor l in range(L):# Moving average of the gradients. Inputs: "v, grads, beta1". Output: "v".### START CODE HERE ### (approx. 2 lines)v["dW" + str(l+1)] = beta1*v["dW" + str(l+1)] + (1-beta1)*grads['dW' + str(l+1)]v["db" + str(l+1)] = beta1*v["db" + str(l+1)] + (1-beta1)*grads['db' + str(l+1)]### END CODE HERE #### Compute bias-corrected first moment estimate. Inputs: "v, beta1, t". Output: "v_corrected".### START CODE HERE ### (approx. 2 lines)v_corrected["dW" + str(l+1)] = v["dW" + str(l+1)]/(1-np.power(beta1,t))v_corrected["db" + str(l+1)] = v["db" + str(l+1)]/(1-np.power(beta1,t))### END CODE HERE #### Moving average of the squared gradients. Inputs: "s, grads, beta2". Output: "s".### START CODE HERE ### (approx. 2 lines)s["dW" + str(l+1)] = beta2*s["dW" + str(l+1)] + (1-beta2)*grads['dW' + str(l+1)]**2s["db" + str(l+1)] = beta2*s["db" + str(l+1)] + (1-beta2)*grads['db' + str(l+1)]**2### END CODE HERE #### Compute bias-corrected second raw moment estimate. Inputs: "s, beta2, t". Output: "s_corrected".### START CODE HERE ### (approx. 2 lines)s_corrected["dW" + str(l+1)] = s["dW" + str(l+1)]/(1-np.power(beta2,t))s_corrected["db" + str(l+1)] = s["db" + str(l+1)]/(1-np.power(beta2,t))### END CODE HERE #### Update parameters. Inputs: "parameters, learning_rate, v_corrected, s_corrected, epsilon". Output: "parameters".### START CODE HERE ### (approx. 2 lines)parameters["W" + str(l+1)] = parameters["W" + str(l+1)] - learning_rate*v_corrected["dW" + str(l+1)]/(np.sqrt(s_corrected["dW" + str(l+1)])+epsilon)parameters["b" + str(l+1)] = parameters["b" + str(l+1)] - learning_rate*v_corrected["db" + str(l+1)]/(np.sqrt(s_corrected["db" + str(l+1)])+epsilon)### END CODE HERE ###return parameters, v, s

5. 不同优化算法下的模型

数据集：使用以下数据集进行测试

3层神经网络模型：

• Mini-batch Gradient Descent:：
  使用函数 update_parameters_with_gd()
• Mini-batch Momentum:：
  使用函数 initialize_velocity() 和 update_parameters_with_momentum()
• Mini-batch Adam：
  使用函数 initialize_adam() 和 update_parameters_with_adam()

def model(X, Y, layers_dims, optimizer, learning_rate = 0.0007, mini_batch_size = 64, beta = 0.9,beta1 = 0.9, beta2 = 0.999,  epsilon = 1e-8, num_epochs = 10000, print_cost = True):"""3-layer neural network model which can be run in different optimizer modes.Arguments:X -- input data, of shape (2, number of examples)Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)layers_dims -- python list, containing the size of each layerlearning_rate -- the learning rate, scalar.mini_batch_size -- the size of a mini batchbeta -- Momentum hyperparameterbeta1 -- Exponential decay hyperparameter for the past gradients estimates beta2 -- Exponential decay hyperparameter for the past squared gradients estimates epsilon -- hyperparameter preventing division by zero in Adam updatesnum_epochs -- number of epochsprint_cost -- True to print the cost every 1000 epochsReturns:parameters -- python dictionary containing your updated parameters """L = len(layers_dims)             # number of layers in the neural networkscosts = []                       # to keep track of the costt = 0                            # initializing the counter required for Adam updateseed = 10                        # For grading purposes, so that your "random" minibatches are the same as ours# Initialize parametersparameters = initialize_parameters(layers_dims)# Initialize the optimizerif optimizer == "gd":pass # no initialization required for gradient descentelif optimizer == "momentum":v = initialize_velocity(parameters)elif optimizer == "adam":v, s = initialize_adam(parameters)# Optimization loopfor i in range(num_epochs):# Define the random minibatches. We increment the seed to reshuffle differently the dataset after each epochseed = seed + 1minibatches = random_mini_batches(X, Y, mini_batch_size, seed)for minibatch in minibatches:# Select a minibatch(minibatch_X, minibatch_Y) = minibatch# Forward propagationa3, caches = forward_propagation(minibatch_X, parameters)# Compute costcost = compute_cost(a3, minibatch_Y)# Backward propagationgrads = backward_propagation(minibatch_X, minibatch_Y, caches)# Update parametersif optimizer == "gd":parameters = update_parameters_with_gd(parameters, grads, learning_rate)elif optimizer == "momentum":parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)elif optimizer == "adam":t = t + 1 # Adam counterparameters, v, s = update_parameters_with_adam(parameters, grads, v, s,t, learning_rate, beta1, beta2,  epsilon)# Print the cost every 1000 epochif print_cost and i % 1000 == 0:print ("Cost after epoch %i: %f" %(i, cost))if print_cost and i % 100 == 0:costs.append(cost)# plot the costplt.plot(costs)plt.ylabel('cost')plt.xlabel('epochs (per 100)')plt.title("Learning rate = " + str(learning_rate))plt.show()return parameters

5.1 Mini-batch梯度下降

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

表现：

Accuracy: 0.79 （Mini-batch梯度下降）

5.2 带动量的Mini-batch梯度下降

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Momentum optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

表现：

Accuracy: 0.79（带动量的Mini-batch梯度下降）

本例子由于太过简单，所以动量的优势没有体现出来，在大的数据集上会较不带动量的模型更好

5.3 带Adam的Mini-batch梯度下降

# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")# Predict
predictions = predict(train_X, train_Y, parameters)# Plot decision boundary
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

表现：

Accuracy: 0.9366666666666666（带Adam的Mini-batch梯度下降）

5.4 对比总结

优化方法	准确率	cost shape
Gradient descent	79.7%	振荡（我的结果是光滑）
Momentum	79.7%	振荡 （我的结果是光滑，求指点）
Adam	94%	更光滑

• 动量Momentum 通常是有帮助的，但是 较小的学习率 和 过于简单的数据集，优势体现不出来
• Adam，明显优于 mini-batch梯度下降 和 动量
• 如果运行更多的迭代次数，三种方法都会产生非常好的结果。但是 Adam 收敛更快
• Adam优点：
  相对较低的内存要求（虽然比 梯度下降 和 动量梯度下降更高）
  即使很少调整超参数（除了𝛼 学习率），通常也能很好地工作

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！