关键词

• 分类模型、回归模型

• 存在序的离散属性、不存在序的离散属性

• 有监督的机器学习

• 回归的分类（输入变量数目，输入变量和输出变量的关系）

• 已知数据集，未知参数

• 均方误差最小化，最小二乘法

• 一元线性回归

• 多元线性回归

一、什么是回归分析

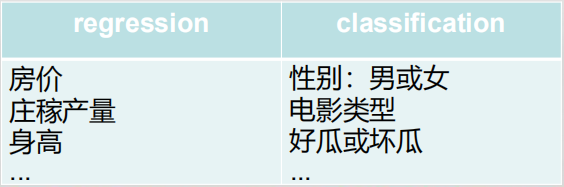
• 分类模型的输出值是离散的 classification
• 回归模型的输出值是连续的 regression
  

倘若在离散属性之间存在序的关系，可通过连续化，将其转化为连续值。

倘若在离散属性之间不存在序的关系，假设为 k 个属性值，通常将其转化为 k 维向量。

回归用于预测输入变量和输出变量之间的关系。回归模型表示从输入变量到输出变量之间映射的函数。并且可以利用这个映射函数尽可能准确地预测出新输入变量的相应输出变量。

因为数据集是有标签的，因而回归是一个有监督的学习过程。

按照输入变量的数目，可以将回归分为单元回归和多元回归
按照输入变量和输出变量之间的关系，可以将其分为线性回归和非线性回归

二、线性模型的基本形式

线性模型：

给定由 d 个属性描述的实例，
$x=(x_1,x_2,...,x_d)$
给定 $\omega$ 表示各属性在预测中的重要性，
$\omega =({\omega }_1,{\omega }_2,...,{\omega }_d)$

此处，我们常常将向量看做是列向量(n*1)

三、线性模型的任务

在我看来，就是利用已知的数据集，确定出合适的参数，已达到要求的预测效果

四、一元线性回归

线性回归的公式为
$f(x)={\omega }^{T}x+b$，其中 $\omega =({\omega }_1,{\omega }_2,...,{\omega }_d),x=(x_1,x_2,...,x_d)$
当为一元线性回归时，$d=1$，
即$f(x)=\omega x+b$

五、多元线性回归

六、检验

七、应用场景