机器学习中的泛化，泛化即是，模型学习到的概念在它处于学习的过程中时模型没有遇见过的样本时候的表现。在机器学习领域中，当我们讨论一个机器学习模型学习和泛化的好坏时，我们通常使用术语：过拟合和欠拟合。我们知道模型训练和测试的时候有两套数据，训练集和测试集。在对训练数据进行拟合时，需要照顾到每个点，而其中有一些噪点，当某个模型过度的学习训练数据中的细节和噪音，以至于模型在新的数据上表现很差，这样的话模型容易复杂，拟合程度较高，造成过拟合。而相反如果值描绘了一部分数据那么模型复杂度过于简单，欠拟合指的是模型在训练和预测时表现都不好的情况，称为欠拟合。

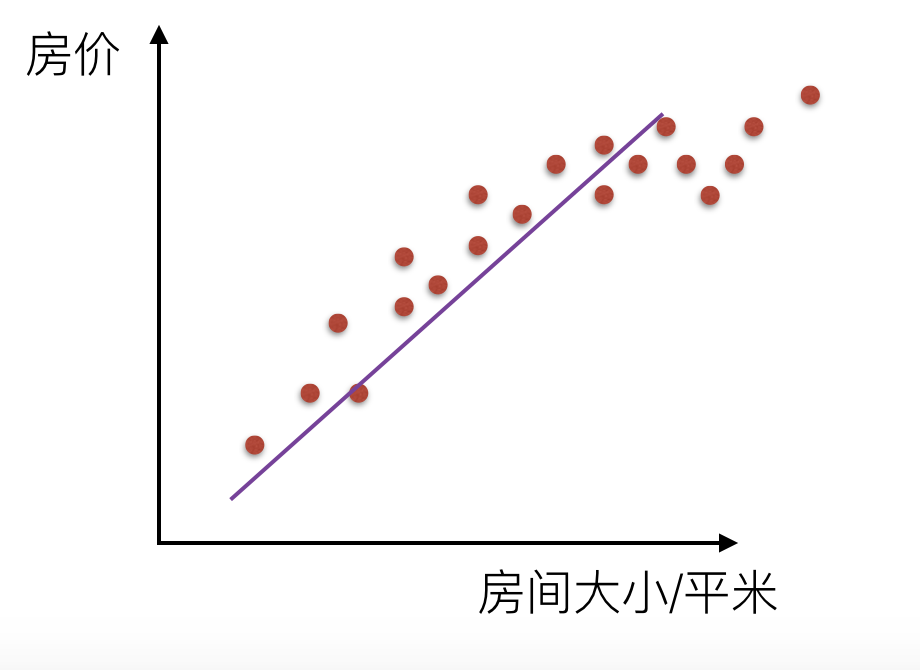
我们来看一下线性回归中拟合的几种情况图示：

$$\theta_0+\theta_1{x}$$

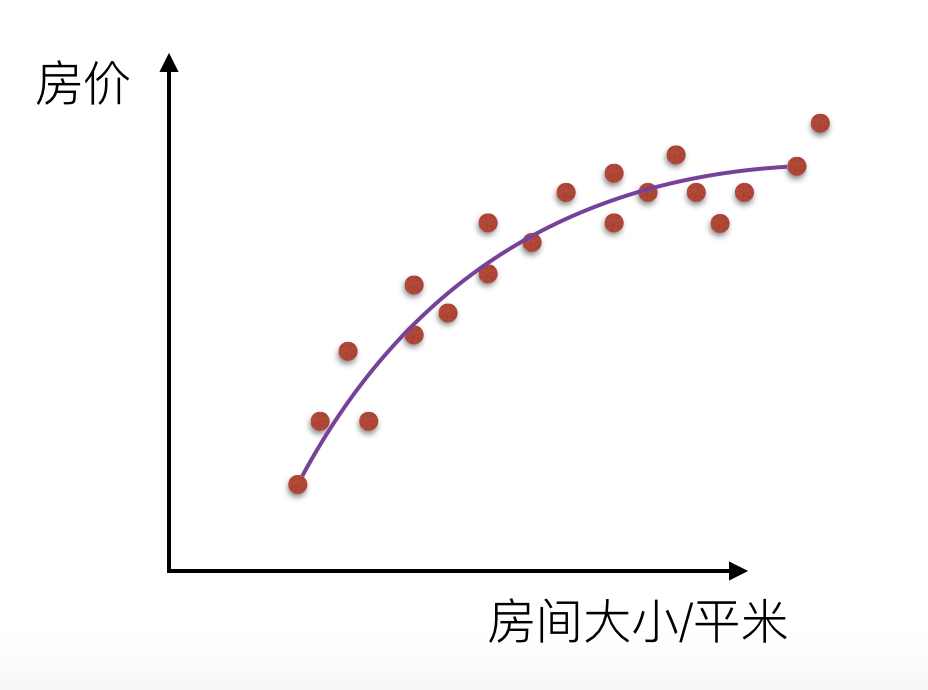
$$\theta{0}+\theta{1}{x}+\theta_{2}x^{2}$$

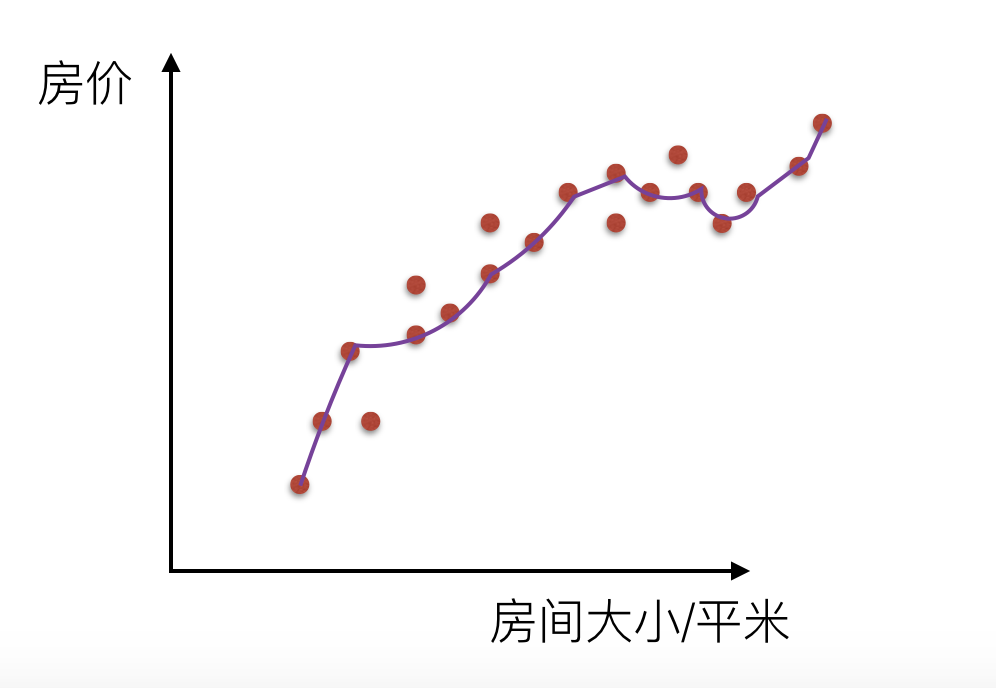
$$\theta{0}+\theta{1}{x}+\theta{2}x^{2}+\theta{3}x^{3}+\theta_{4}x^{4}$$

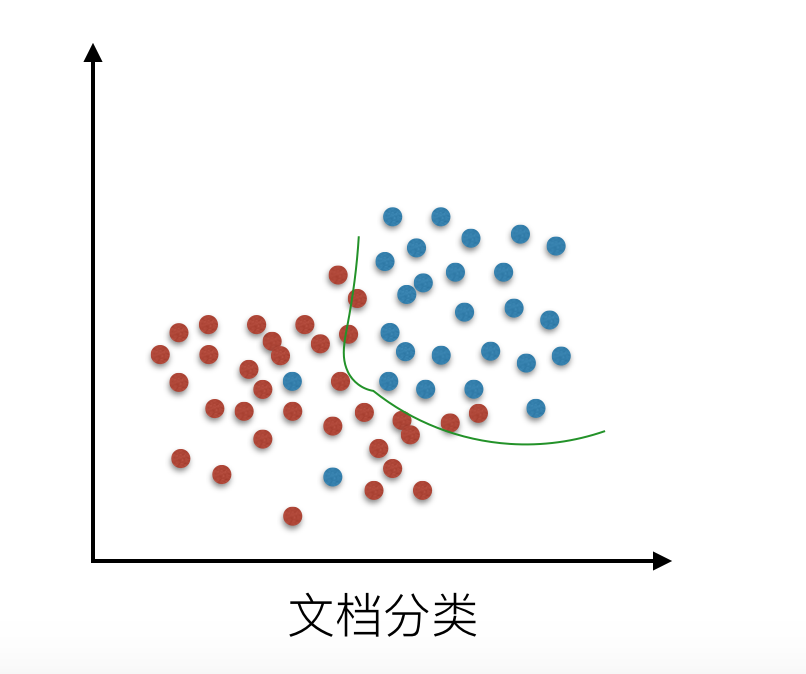
还有在逻辑回归分类中的拟合情况：

解决过拟合的方法

在线性回归中，对于特征集过小的情况，容易造成欠拟合（underfitting），对于特征集过大的情况，容易造成过拟合（overfitting）。针对这两种情况有了更好的解决办法

欠拟合

欠拟合指的是模型在训练和预测时表现都不好的情况，欠拟合通常不被讨论，因为给定一个评估模型表现的指标的情况下，欠拟合很容易被发现。矫正方法是继续学习并且试着更换机器学习算法。

过拟合

对于过拟合，特征集合数目过多，我们需要做的是尽量不让回归系数数量变多，对拟合（损失函数）加以限制。

（1）当然解决过拟合的问题可以减少特征数，显然这只是权宜之计，因为特征意味着信息，放弃特征也就等同于丢弃信息，要知道，特征的获取往往也是艰苦卓绝的。

（2）引入了 正则化 概念。

直观上来看，如果我们想要解决上面回归中的过拟合问题，我们最好就要消除$$x_3$$和$$x_4$$的影响，也就是想让$$\theta_3{,}\theta_4$$都等于0，一个简单的方法就是我们对$$\theta_3{,}\theta_4$$进行惩罚，增加一个很大的系数，这样在优化的过程中就会使这两个参数为零。
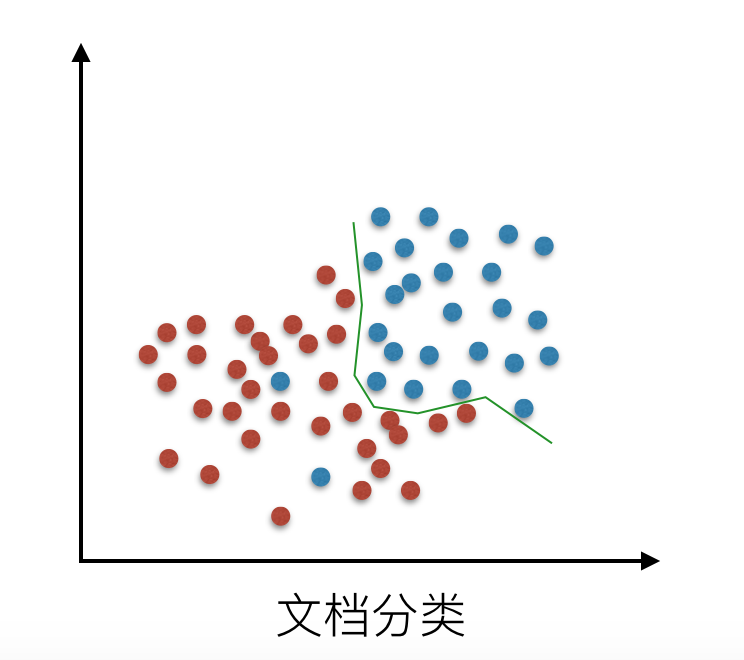
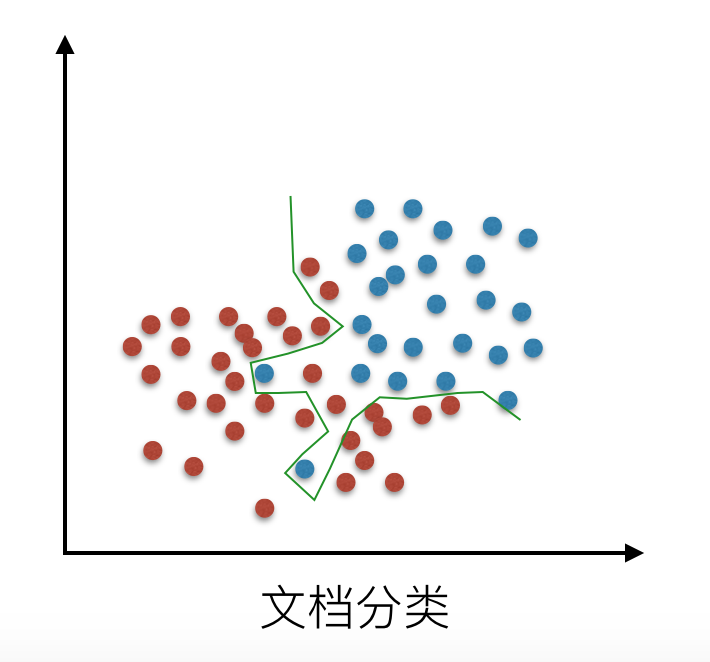