1. 题目

给你一个由正整数组成的数组 nums 。

数字序列的 最大公约数 定义为序列中所有整数的共有约数中的最大整数。

例如，序列 [4,6,16] 的最大公约数是 2 。
数组的一个 子序列 本质是一个序列，可以通过删除数组中的某些元素（或者不删除）得到。

例如，[2,5,10] 是 [1,2,1,2,4,1,5,10] 的一个子序列。
计算并返回 nums 的所有 非空 子序列中 不同 最大公约数的 数目 。

示例 1：

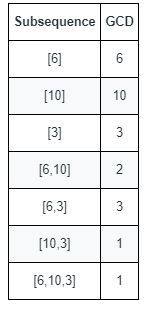
输入：nums = [6,10,3]
输出：5
解释：上图显示了所有的非空子序列与各自的最大公约数。
不同的最大公约数为 6 、10 、3 、2 和 1 。示例 2：
输入：nums = [5,15,40,5,6]
输出：7提示：
1 <= nums.length <= 10^5
1 <= nums[i] <= 2 * 10^5

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/number-of-different-subsequences-gcds
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

• 不能枚举子序列，2^n 很大
• 枚举 最大公约数 g ，参考题解区

class Solution {
public:int countDifferentSubsequenceGCDs(vector<int>& nums) {int maxnum = *max_element(nums.begin(), nums.end());vector<int> hasnum(maxnum+1, false);//数字是否存在for(auto n : nums){hasnum[n] = true;}int count = 0;for(int g = 1; g <= maxnum; g++)//枚举最大公约数{int gcd = -1;//实际的公约数for(int num = g; num <= maxnum; num += g){   // 枚举 公约数 g 的倍数的 numif(hasnum[num])// num 存在{if(gcd == -1)gcd = num;elsegcd = __gcd(num, gcd);//序列的最大公约数if(gcd <= g)// = 找到了序列的 最大公约数 gcd 为 g// < gcd 不会变大, 停止搜索break;}}if(gcd == g)count++;}return count;}
};

328 ms 95.9 MB C++

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！