同学你好！本文章于2021年末编写，获得广泛的好评！

故在2022年末对本系列进行填充与更新，欢迎大家订阅最新的专栏，获取基于Pytorch1.10版本的理论代码(2023版)实现，

Pytorch深度学习·理论篇(2023版)目录地址为：

CSDN独家 | 全网首发 | Pytorch深度学习·理论篇(2023版)目录本专栏将通过系统的深度学习实例，从可解释性的角度对深度学习的原理进行讲解与分析，通过将深度学习知识与Pytorch的高效结合，帮助各位新入门的读者理解深度学习各个模板之间的关系，这些均是在Pytorch上实现的，可以有效的结合当前各位研究生的研究方向，设计人工智能的各个领域，是经过一年时间打磨的精品专栏！https://v9999.blog.csdn.net/article/details/127587345欢迎大家订阅(2023版)理论篇

以下为2021版原文~~~~

1 卷积神经网络接口

1.1 卷积接口介绍

• torch.nn.functional.conv1d：实现按照1个维度进行的卷积操作，常用于处理序列数据。
• torch.nn.functional.conv2d：实现按照2个维度进行的卷积操作，常用于处理二维平面图片。
• torch.nn.functional.conv3d：实现按照3个维度进行的卷积操作，常用于处理三维图形数据。

1.2 卷积函数的定义

torch.nn.functional.conv2d(input, weight, bias=None, stride=1, padding=0, dilation=1, groups=1) 

• input：输入图像的大小(minibatch，in_channels，H，W)，是一个四维tensor
• filters：卷积核的大小(out_channels，in_channe/groups，H，W)，是一个四维tensor
• bias：每一个channel的bias，是一个维数等于out_channels的tensor
• stride：一个数或者一个二元组(SH，SW)，代表纵向和横向的步长
• padding：一个数或者一个二元组(PH，PW )，代表纵向和横向的填充值
• dilation：一个数，代表卷积核内部每个元素之间间隔元素的数目(不常用，默认为0)
• groups：一个数，代表分组卷积时分的组数，特别的当groups = in_channel时，就是在做逐层卷积(depth-wise conv).

1.2 卷积函数的类实现

class torch.nn.Conv2d(in_channels, out_channels, kennel_size, stride=1, padding=0, dilation=1, groups=1, bias=true)

• in_channels(int) 输入特征图的通道数
• out_channels(int) 输出特征图的通道数
• kenal_size(int or tuple) 卷积核大小
• stride(int or tuple, optional) 卷积核的步长，默认为1
• padding(int or tuple,optional) 输入的每一条边补充0的层数，默认为0
• dilation(int or tuple, optional) 卷积核元素间的距离，默认为1
• groups(int,optional)将原始输入通道划分成的组数，默认为1
• bias(bool,optional) 默认为True，表示输出的bias可学习
   

1.3 两者区别

torch.nn.Conv2D是一个类，而torch.nn.functional.conv2d是一个函数，在Sequential里面只能放nn.xxx，而nn.functional.xxx是不能放入Sequential里面的。

nn.Module 实现的 layer 是由 class Layer(nn.Module) 定义的特殊类，nn.functional 中的函数是纯函数，由 def function(input) 定义。

nn.functional.xxx 需要自己定义 weight，每次调用时都需要手动传入 weight，而 nn.xxx 则不用。

1.4 卷积函数的操作步骤

1.5 卷积操作的类型

1.5.1 窄卷积(vaild卷积)

即生成的特征图比原来的原始图片小。它的步长是可变的。假如，滑动步长为S,原始图片的维度为N1×N1。卷积核的大小为卷积后图像大小为[(N1-N2)/S + 1]。

1.5.2 同卷积(same卷积)，

卷积后的图片尺寸与原始的一样大，同卷积的步长是固定的，滑动步长为1。一般操作时都要使用padding操作（在原始图片的外围补0，来确保生成的尺寸不变)。

1.5.3 全卷积(full卷积)，也称反卷积，主要用作反卷积网络中，用于图像的恢复与还原。

将原始图片里面的每个像素点都用卷积操作展开。如图7-16所示，白色的块是原始图片，浅色的是卷积核，深色的是正在卷积操作的像素点。在全卷积操作的过程中，同样需要对原有图片进行padding操作，生成的结果会比原有的图片尺寸大。步长固定为1，卷积核的大小为卷积后图像大小为[N1-N2-1]

2 卷积函数的使用

2.1 定义卷积输入变量 --- CNN_New.py(第01部分)

import torch### 1.1 定义输入变量
# [batch,in_channels,in_height,in_width]
# [训练时一个batch的图片数量，图像通道数，图片高度，图片宽度]
input1 = torch.ones([1,1,5,5])
input2 = torch.ones([1,2,5,5])
input3 = torch.ones([1,1,4,4])

2.2 验证卷积的补0规则 --- CNN_New.py(第02部分)

### 1.2 验证补0规则
# 设置padding为1，在输入数据上补1排0
padding1 = torch.nn.functional.conv2d(input1,torch.ones([1,1,1,1]),stride=1,padding=1)
print(padding1)
# 设置padding为1，在输入数据上补2行0
padding2 = torch.nn.functional.conv2d(input1,torch.ones([1,1,1,1]),stride=1,padding=(1,2))
print(padding2)

tensor([[[[0., 0., 0., 0., 0., 0., 0.],
          [0., 1., 1., 1., 1., 1., 0.],
          [0., 1., 1., 1., 1., 1., 0.],
          [0., 1., 1., 1., 1., 1., 0.],
          [0., 1., 1., 1., 1., 1., 0.],
          [0., 1., 1., 1., 1., 1., 0.],
          [0., 0., 0., 0., 0., 0., 0.]]]])
tensor([[[[0., 0., 0., 0., 0., 0., 0., 0., 0.],
          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
          [0., 0., 1., 1., 1., 1., 1., 0., 0.],
          [0., 0., 0., 0., 0., 0., 0., 0., 0.]]]])

2.3 卷积核的定义 --- CNN_New.py(第03部分)

### 1.3 定义卷积核变量
# [out_channels,in_channels,filter_height,filter_width]
# [卷积核个数,图像通道数,卷积核的高度,卷积核的宽度
filter1 = torch.tensor([-1.0,0,0,-1]).reshape([1,1,2,2]) # 1通道输入和1通道输出的2X2矩阵
filter2 = torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1]).reshape([2,1,2,2])# 1通道输入和2通道输出的2X2矩阵
filter3 = torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1,-1.0,0,0,-1]).reshape([3,1,2,2])# 1通道输入和3通道输出的2X2矩阵
filter4 = torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1,-1.0,0,0,-1,-1.0,0,0,-1]).reshape([2,2,2,2])# 2通道输入和2通道输出的2X2矩阵
filter5 = torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1]).reshape([1,2,2,2]) # 2通道输入和1通道输出的2X2矩阵

2.4 卷积操作与其结果 --- CNN_New.py(第04部分)

### 1.4 卷积操作
## 1个通道输入，生成1个特征图(卷积核个数)
pl1 = torch.nn.functional.conv2d(input1,filter1,stride=2,padding=1)
print("p1",pl1)
## 1个通道输入，生成2个特征图(卷积核个数)
pl2 = torch.nn.functional.conv2d(input1,filter2,stride=2,padding=1)
print("p2",pl2)
## 1个通道输入，生成3个特征图(卷积核个数)
pl3 = torch.nn.functional.conv2d(input1,filter3,stride=2,padding=1)
print("p3",pl3)
## 2个通道输入，生成2个特征图(卷积核个数)
pl4 = torch.nn.functional.conv2d(input2,filter4,stride=2,padding=1)
print("p4",pl4)
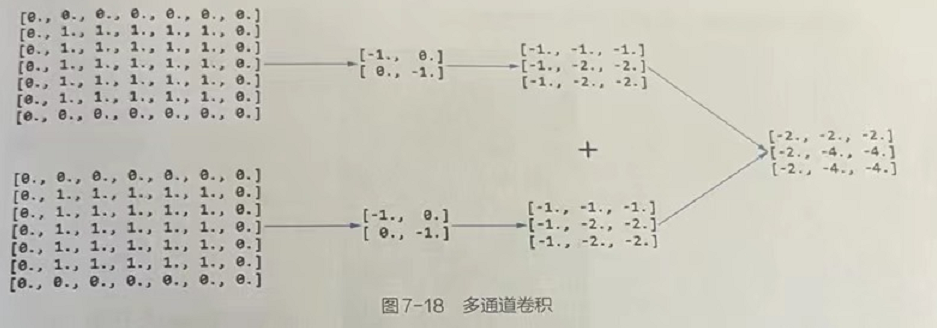
## 2个通道输入，生成1个特征图(卷积核个数)====》对于卷积核对多通道输入的卷积处理，多通道的结果的叠加
pl5 = torch.nn.functional.conv2d(input2,filter5,stride=2,padding=1)
print("p5",pl5)
## padding不同，生成的结果也不同
pl6 = torch.nn.functional.conv2d(input1,filter1,stride=2,padding=0)
print("p6",pl6)

p1 tensor([[[[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]]]])
p2 tensor([[[[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]],

         [[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]]]])
p3 tensor([[[[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]],

         [[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]],

         [[-1., -1., -1.],
          [-1., -2., -2.],
          [-1., -2., -2.]]]])
p4 tensor([[[[-2., -2., -2.],
          [-2., -4., -4.],
          [-2., -4., -4.]],

         [[-2., -2., -2.],
          [-2., -4., -4.],
          [-2., -4., -4.]]]])
p5 tensor([[[[-2., -2., -2.],
          [-2., -4., -4.],
          [-2., -4., -4.]]]])
p6 tensor([[[[-2., -2.],
          [-2., -2.]]]])

Tip：多通道卷积的图解

2.5 代码汇总

import torch### 1.1 定义输入变量
# [batch,in_channels,in_height,in_width]
# [训练时一个batch的图片数量，图像通道数，图片高度，图片宽度]
input1 = torch.ones([1,1,5,5])
input2 = torch.ones([1,2,5,5])
input3 = torch.ones([1,1,4,4])### 1.2 验证补0规则
# 设置padding为1，在输入数据上补1排0
padding1 = torch.nn.functional.conv2d(input1,torch.ones([1,1,1,1]),stride=1,padding=1)
print(padding1)
# 设置padding为1，在输入数据上补2行0
padding2 = torch.nn.functional.conv2d(input1,torch.ones([1,1,1,1]),stride=1,padding=(1,2))
print(padding2)### 1.3 定义卷积核变量
# [out_channels,in_channels,filter_height,filter_width]
# [卷积核个数,图像通道数,卷积核的高度,卷积核的宽度
filter1 = torch.tensor([-1.0,0,0,-1]).reshape([1,1,2,2]) # 1通道输入和1通道输出的2X2矩阵
filter2 = torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1]).reshape([2,1,2,2])# 1通道输入和2通道输出的2X2矩阵
filter3 = torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1,-1.0,0,0,-1]).reshape([3,1,2,2])# 1通道输入和3通道输出的2X2矩阵
filter4 = torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1,-1.0,0,0,-1,-1.0,0,0,-1]).reshape([2,2,2,2])# 2通道输入和2通道输出的2X2矩阵
filter5 = torch.tensor([-1.0,0,0,-1,-1.0,0,0,-1]).reshape([1,2,2,2]) # 2通道输入和1通道输出的2X2矩阵### 1.4 卷积操作
## 1个通道输入，生成1个特征图(卷积核个数)
pl1 = torch.nn.functional.conv2d(input1,filter1,stride=2,padding=1)
print("p1",pl1)
## 1个通道输入，生成2个特征图(卷积核个数)
pl2 = torch.nn.functional.conv2d(input1,filter2,stride=2,padding=1)
print("p2",pl2)
## 1个通道输入，生成3个特征图(卷积核个数)
pl3 = torch.nn.functional.conv2d(input1,filter3,stride=2,padding=1)
print("p3",pl3)
## 2个通道输入，生成2个特征图(卷积核个数)
pl4 = torch.nn.functional.conv2d(input2,filter4,stride=2,padding=1)
print("p4",pl4)
## 2个通道输入，生成1个特征图(卷积核个数)====》对于卷积核对多通道输入的卷积处理，多通道的结果的叠加
pl5 = torch.nn.functional.conv2d(input2,filter5,stride=2,padding=1)
print("p5",pl5)
## padding不同，生成的结果也不同
pl6 = torch.nn.functional.conv2d(input1,filter1,stride=2,padding=0)
print("p6",pl6)