1、常见的集成思想

bagging：基学习器之间并行训练，且学习器之间没有依赖，像是集体决策的过程，每个个体都进行单独学习，再通过投票的方式做最后的集体决策。常见的算法有随机森林

boosting：基学习器之间串行训练，且学习器之间存在依赖，将基学习器层层叠加，每一层在训练的时候，对前一层基学习器分错的样本给予更高的权重。类似于人类的学习过程，对于错误，进行加强学习，直到犯错误的次数减少到很低的程度。常见的算法有AdaBoost、GBDT、XGBoost。

Stacking:首先使用原始数据训练出一级学习器，将一级学习器的输出作为输入并使用对应原始标记作为新标记，组成新的数据集来训练二级学习器（结合学习器）。常用于模型融合。

2、从偏差和方差的角度解释Bagging和Boosting

偏差是由于分类器的表达能力有限导致的系统性错误；

方差是由于分类器对于样本分布过于敏感，导致在训练样本数较少时，产生过拟合；

bagging是采用分而治之策略，通过对训练样本进行多次采样，并分别训练出不同模型，然后做综合，减小集成分类器之间的方差。

boosting是通过逐步聚焦于基学习器分错的样本，减小集成分类器的偏差。

2、随机森林的随机性？

数据集：有放回随机取样

特征：随机选取特征，进行分割点计算

3、Adboost、提升树（boosting tree），梯度提升树的异同？

相同：

• 加法模型：模型是基学习器进行累加，得到一个最终的加法模型。
• 前向分步算法：从前向后，每一步只学习一个基函数及其系数，逐步逼近优化目标函数，简化优化的复杂度。

区别：

Adaboost的实现步骤：

（1）初始化权重分布，假设模型有均匀的权值分布。

（2）对数据进行学习，计算Gm（分类器）在训练数据集上的分类误差率，

（3）计算Gm（分类器）系数，系数代表在最终分类器上的重要性。

（4）更新权重（m步的权重分布），

（5）对基学习器进行累加，组成线性组合，得到最终的分类器：

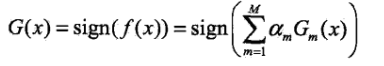
注释：I(x)是指示函数，sign(x)是符号函数。

,

提升树（Boosting Tree）的实现步骤:

提升方法实际采用加法模型和前向分布算法，以决策树为基函数的提升方法称为提升树，对分类问题决策树是二叉分类树，损失函数时指数损失，对于回归问题决策树是二叉回归树，损失函数是均方损失。

分析：

其中，r是当前模型拟合数据的残差。

梯度提升树（Gradient boosting DT）：

将当前模型损失函数的负梯度作为残差的近似替换值。

4、RF和GBDT的区别

相同点：都用了集成思想

不同点：

• RF是bagging思想，减小了方差，GBDT是boosting思想，减小了偏差
• RF是串行，GBDT是并行
• RF是分类和回归树，GBDT只能回归树
• RF是采用投票进行最终决策，GBDT是多棵树累加决策
• RF对异常值不敏感，且不需要归一化，GBDT对异常值敏感（串行），需要归一化（GBDT的树是在上一颗树的基础上通过梯度下降求解最优解，归一化能收敛的更快，而随机森林本来就是通过减少方差提高性能的，树之间建立关系是独立的，不需要归一化）

5、GBDT的缺点？

• 在高维稀疏的数据集上，表现性不好。
• 训练过程是串行，需要在决策树内部采用一些局部并行的手段提高训练速度。

6、GBDT和XGBoost的异同？

不同：

• GBDT用了一阶导数信息，XGBoost用了一阶、二阶导数信息
• GBDT不执行并行化，XGBoost在数据和特征方便增加了并行化处理，（数据采样、特征重要性排序）
• GBDT对异常值敏感，XGBoost新增了缺失值处理策略
• GBDT只能是树模型，XGBoost可以自定义基学习器
• XGBoost增加了正则化的策略

7、Xgboost 如何寻找最优特征？是有放回还是无放回呢？

Xgboost在训练的过程中给出各个特征的增益评分，最大增益的特征会被选出来作为分裂依据，从而记忆了每个特征对在模型训练时的重要性。从根到叶子中间节点涉及某特征的次数作为该特征重要性排序。Xgboost是不放回，还支持子采样和列采样。

8、Xgboost为什么要用泰勒展开，优势在哪里？

XGBoost使用了一阶和二阶偏导，二阶导数有利于梯度下降的更快更准，使用泰勒展开取得函数做自变量的二阶导数形式，可以再不选定损失函数具体形式的情况下，仅仅依靠输入数据的值就可以进行叶子分裂优化算法，本质上将损失函数的选取和模型算法优化/参数选择分开，这种去耦合增强了XGBoost的适用性，使得模型按需选取损失函数。

9、RF如何处理缺失值？

方法一：将数值型变量中的缺失值用其所对应类别中的中位数替换。把描述型变量缺失的部分用所对应类别出现最多的数值替代。

方法二：在方法一的基础上做了升级，引入了权重变量，即对需要替换的数据先和其他数据做相似度测量，如果是分类变量，则用没有缺失的观测实例相似度的权重投票，如果是连续型变量，则用加权平均和进行填充。

10、XGBoost如何处理缺失值？

xgboost把缺失值当做稀疏矩阵来对待，本身的在节点分裂时不考虑的缺失值的数值。缺失值数据会被分到左子树和右子树分别计算损失，选择较优的那一个。如果训练中没有数据缺失，预测时出现了数据缺失，那么默认被分类到右子树。

11、随机森林如何评估特征重要性？

12、XGBoost如何给特征评分？

在CART树中，通过基尼指数选取分离点的特征，一个特征被选中的次数越多，该特征的评分就越高。

在XGboost中，枚举不同的树结构，利用打分函数来寻找最优的结构树。从树深度0开始，每个节点遍历所有特征，对于单个特征，首先对特征的值进行排序，然后线性扫描该特征进行选择最好的切割点，再比较所有的特征，选择信息增益增高的特征为当前节点。

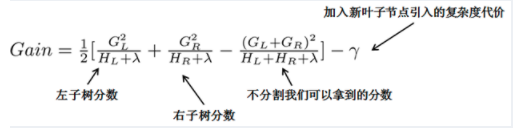
假设年龄这个特征，我们首先对年龄进行排序，设定阈值a，将小于阈值a的分为一类，大于阈值a的分为一类，计算该特征的基尼指数，若存在多个阈值，就会出现多个基尼指数值，选择最大的那个为当前的阈值，并计算所有特征（年龄、性别、职业等），选择最大的gini指数的特征为当前节点。这种只看到当前节点的思想就是greddy exact。

引入新叶子的惩罚项是为了优化目标函数，对应了树的剪枝，当分割阈值小于惩罚项，就忽略这个分割。