借汉诺塔理解栈与递归

我们先说，在一个函数中，调用另一个函数。

首先，要意识到，函数中的代码和平常所写代码一样，也都是要执行完的，只有执行完代码，或者遇到return，才会停止。

那么，我们在函数中调用函数，执行完了，就会重新回到本函数中，继续向下执行，直到结束。

在执行其它函数时，本函数相当于中断了，不执行了。那我们重新回来的时候，要从刚才暂停的地方开始，继续执行，这期间，所有现场信息都要原封不动，就相当于时间暂停了一样，什么都不能改变，这样才能做到程序的准确。

所以，通常，在执行另一个函数之前，电脑会将现场信息压入一个系统栈，为被调用的函数分配存储区，然后开始执行被调函数。执行完毕后，保存计算结果，释放被调函数的空间，按照被调函数里保存的返回地址，返回到原函数。

那什么是递归函数呢？

就是多个函数嵌套调用。不同的是，这些函数是同一个函数，只是参数可能不同，甚至参数也一样，只是存储空间不同。

每一层递归所需信息构成一个栈，每一块内存储着所有实在参数，所有局部变量，上一层的返回地址，等等一切现场信息。每执行完就弹出。

递归函数有着广泛应用，主要适合可以把自身分化成一样的子问题的问题。比如汉诺塔。

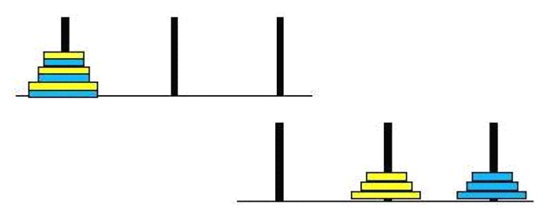
汉诺塔：汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

思路：函数（n,a,b,c)含义是把n个盘子从a柱子搬到c柱子的方法

一个盘子，直接搬过去。

多个盘子，我们把n-1个盘子都移动到另一个柱子上，把最大的搬过去然后把剩下的搬过去。

def hanoi(n, a, b, c):if n == 1:print(a, '-->', c)else:hanoi(n - 1, a, c, b)print(a, '-->', c)hanoi(n - 1, b, a, c)
# 调用
hanoi(3, 'A', 'B', 'C')

结果：

A --> C
A --> B
C --> B
A --> C
B --> A
B --> C
A --> C

我们的栈：

第一次：

我们把hanoi(3, 'A', 'B', 'C')存了起来，调用了hanoi(3-1, 'A', 'C', 'B'),现在栈里压入了3, 'A', 'B', 'C'，还有函数执行到的位置等现场信息。然后执行hanoi(3-1, 'A', 'C', 'B')，发现要调用hanoi(3-1-1, 'A', 'B', 'C')，我们又把3-1, 'A', 'C', 'B'等信息压入了栈，现在栈是这样的：

栈头

2, 'A', 'C', 'B'

3, 'A', 'B', 'C'

栈尾

然后执行hanoi(3-1-1, 'A', 'B', 'C')，发现n=1了，打印了第一条A --> C，然后释放掉了hanoi(3-1-1, 'A', 'B', 'C')的空间，并通过记录的返址回到了hanoi(3-1, 'A', 'C', 'B')，然后执行打印语句A --> B，然后发现要调用hanoi(3-1-1, 'C', 'A', 'B')，此时栈又成了：

2, 'A', 'C', 'B'
3, 'A', 'B', 'C'

调用hanoi(1, 'A', 'C', 'B')发现可以直接打印，C --> B。

然后我们又回到了2, 'A', 'C', 'B'这里。发现整个函数执行完了，那就弹出吧。这时栈是这样的：

3, 'A', 'B', 'C'

只有这一个。

我们继续执行这个函数的代码，发现

def hanoi(n, a, b, c):
if n == 1:
print(a, '-->', c)
else:
hanoi(n - 1, a, c, b)//执行到了这里
print(a, '-->', c)
hanoi(n - 1, b, a, c)

那我们就继续执行，发现要打印A --> C

然后继续，发现要调用 hanoi(n - 1, b, a, c)，那我们继续把现场信息压栈，继续执行就好了。

递归就是把大问题分解成小问题进而求解。

具体执行就是通过系统的栈来实现返回原函数的功能。