01知识框架

02图的遍历

1

深度优先遍历基本思想：首先访问图中起始顶点v，然后由v出发，访问与v邻接且未被访问的顶点再访问与v相邻且未被访问的顶点 w1...重复上述过程。当不能再继续向下访问时，依次退回到最近被的问的顶点，若它仍有邻接顶点未被访问过，则从该点开始继续上述搜索过程，直至 图中所有顶点均被切问过为止。所以深度优先遍历的策略就是尽可能“深”的搜索一个图。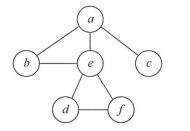

对以上无向图进行深度优先遍历，从a开始：

第1步：访问a

第2步：访问a的邻接点e(这里也可以访问b或c)

第3步：访问e的邻接点f(也可访问d)

第4步：访问f的邻接点d

第5步：此时d无还没有过的邻接点，退回到e，访问b

第6步：此时b也无还未被访问过的邻接点，故访问最后一个点c

因此访问顺序为：a->e->f->d->b->c(答案不唯一)

代码实现如下：(非递归)思想：深度优先遍历图的思想就是从初始顶点开始，一直访问其相邻的结点(在其相邻结点存在情况下)。故可利用一个栈记住上一个访问过的结点，当结点无邻接点时，可以退回到上一个结点，访问上一结点为被访问过的结点，直至所有顶点均被访问。

void  Traver(AdjList g,vertype v){   struct arc *stack[];//初始化栈   visited[v]=1；   printf(v);  //输出顶点v，将该顶点的访问数组对应元素置为1   top=0;    p=g[v].firstarc;    stack[++top]=p; //初始化栈顶元素，将p指向初始顶点，将p入栈   while(top>0 || p!=null) //当栈中有元素或p不为空  {     while (p)     {       if (p && visited[p->adjvex])          p=p->next;       else        {         printf(p->adjvex);          visited[p->adjvex]=1;          stack[++top]=p;          p=g[p->adjvex].firstarc;//将p指向与p的邻接点相邻的第一个元素        }     }     if (top>0)     {      p=stack[top--];       p=p->next;      } //若栈不为空，则退栈并将退栈元素赋给p，使p指向p的下一个邻接点}//[注意] 以上算法适合连通图，若是非连通图，可能有结点未被访问到，则再增加一个主调算法,其核心语句是for (vi=1;vi<=n;vi++) if (!visited[vi]) Traver(g,vi);

(递归)思想：因为每次从顶点依次访问的操作相同，故也可使用递归。

void DFS(ALGraph &G , int v){   ArcNode *p ;  if(visited[v]==0)   {     printf("%c ",G.vertices[v].data); //置访问标志，访问顶点v    }  visited[v]=1;  p=G.vertices[v].firstarc; //链表的第一个结点   while (p!=NULL)  {     if (!visited[p->adjvex])    {       DFS(G, p->adjvex);     } //从v的未访问过的邻接顶点出发深度优先搜索p=p->nextarc ;   }}

2

应用

应用：(选择题使用)

(1)查找图中的路径

(2)寻找连通分量

(3)判断是否有环

---

2

广度优先遍历基本思想：广度优先遍历类似于二叉树的层次遍历。首先访问起始顶点v，然后从v出发依次访问v的各个未访问过的邻接顶点 w1,w2,...然后依次访问w1,w2...的所有未被防问过的邻接顶点,再从这些访问过的顶点出发，访问它们所有未被访问过的邻接顶点，直至图中所有顶点都被访问过为止，此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作为始点，重复上述过程，直至图中所有顶点都被访问到为止。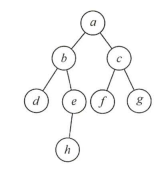

利用广度优先遍历访问上图：

第1步：访问初始顶点a第2步：访问与a相邻的结点b、c第3步：访问与b相邻的结点d、e第4步：访问与c相邻的结点f、g第5步：访问与e相邻的结点h访问顺序为：a->b->c->d->e->f->g->h代码实现：思想：图的广度优先遍历算法是树的层次遍历的扩展，该算法使用了两个函数，一个是广度优先遍历图，一个是广度优先遍历的详细遍历过程。与二叉树的层次遍历类似，详细实现时需要借用一个辅助队列存放每一层的元素，访问其子结点时使用。

bool visited[MAX VERTEX NUM]; //访问标记数组 void BFSTraverse (Graph G) {    for (i=O ; i   visited[i]=FALSE; //访问标记数组初始化   InitQueue(Q) ; //初始化辅助队列    for (i=0; i     if (! visited [i]) //对每个连通分量调用BFS       BFS(G ,i); //vi未被访问过，从vi开始BFSvoid BFS (Graph G, int v ){   //从顶点出发广度优先遍历图   visit(v); //访问初始顶点   visited [v] =TRUE ; //将访问过的顶点做标记  Enqueue( v)  //顶点入队列  while ( ! isEmpty (Q)) {    DeQueue (Q, v ); //顶点出队列   for (w=FirstNeighbor(G,v) ;w>=0; w=NextNeighbor(G,v,w)) {//检测所有v的邻接点     if (! visited [w] )      { //w为v尚未被访问过的邻接点       visit (w); //访问顶点        visited[w ]=TRUE ；//对已访问的顶点做标记        EnQueue (Q, w) ; //将顶点w入队列      }    }  }}

应用：(选择题使用)

(1)查找最短路径

(2)求任意两顶点间的最短路径