只听名字的话会感觉对偶单纯形法和对偶问题关系很大，其实不然(想要了解对偶问题的话可以看我之前的文章)。对偶单纯形法在我看来和大M法以及两阶段法很像，都是用来补充纯粹的单纯形法无法解决特殊问题的缺陷。而且对偶单纯形法更加“强大”，因为它可以在等式右端(b)为负值时直接求解，这也是选择使用它的大多数场景。
接下来以下图中题为例直接进行讲解：
设：对偶法 = 对偶单纯形法第一步： 与单纯形法一样，对偶法第一步仍然是要化成标准形式，但是注意这里化成标准形式时和单纯形法不同。由于对偶法计算时等式右端可以为负值，所以为了简化计算，统一将不等式符号化为“<=”，也就是只添加松弛变量。即原式化为：
相应的单纯形表：
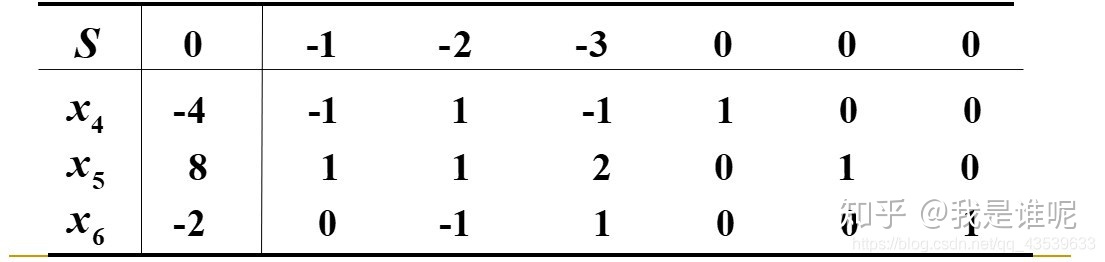
判断对偶法为最优解的方法：左下值(b值)全为正数(也就是-4,8,-2那里)，以及检验数全为非正。
第二步： 如果该基本解不是最优解那么就要进行换基迭代，但是对偶法的迭代法和单纯形法的方式不太一样。回忆下单纯形法的迭代方式(这里以min类型函数为例，我一般都是这样写)：①找检验数中最大的值(假如以上图中的单纯形表为例)，这里要找的值就是-1，然后用x4，x5，x6对应的b值去除以相应的-1下的每一行数(-4/-1，8/1)，注意下我没有写-2/0，因为当要除的数为0时一般就不考虑将该x换出的可能了。然后根据计算出的数值(4,8)取其中最小的数所对应的x，并将其做出基处理。接着说对偶法的换基迭代方式 ，与单纯法所考虑的重点不同，对偶法主要目的是要将b值全部化为正数，因此要优先考虑将b值中最小的数做出基处理，这里选的值为-4，然后用检验数除以该行对应的相应列的数(-1/-1，-3/-1)，注意这里除的时候只有两个需要考虑，因为做除数的值必须要为负值，否则不考虑入基的情况(被除数÷除数)，取最小的值做入基处理，即本题选的是-1，也就是x1。然后进行初等行变换即可，如果达不到最优解的条件就要继续换基迭代。
剩余步骤如下：
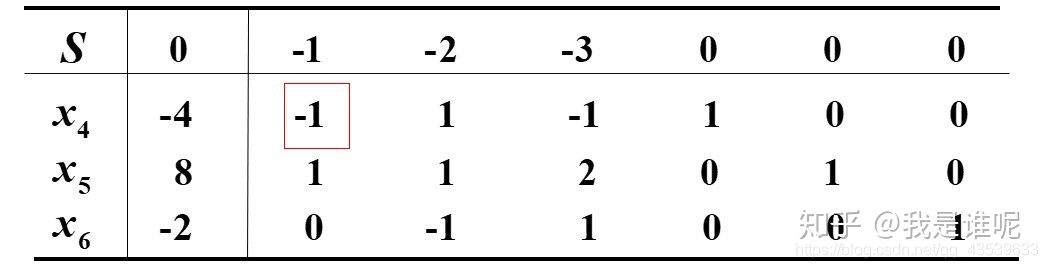
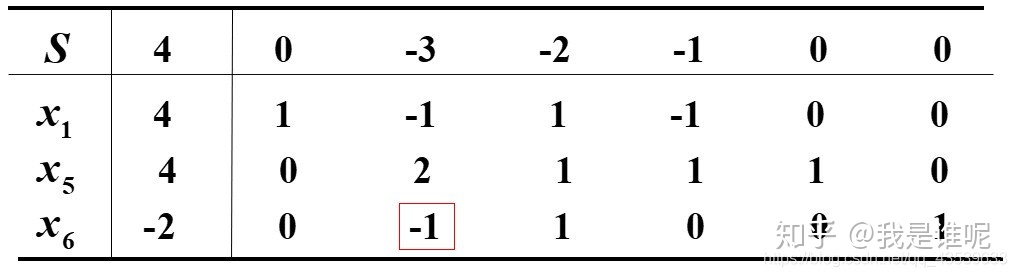
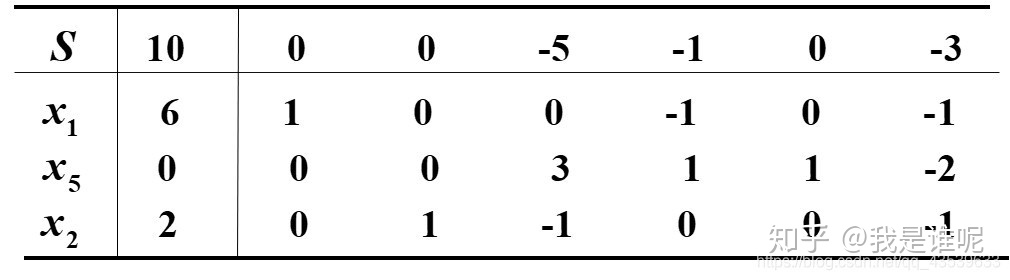
因为b值全都非负，得最优单纯形表，所以得原问题得最优解为x1 = 6，x2 = 2，x3 = 10，最优值为S = 10.
下面再举一个例子，并附上对应步骤：
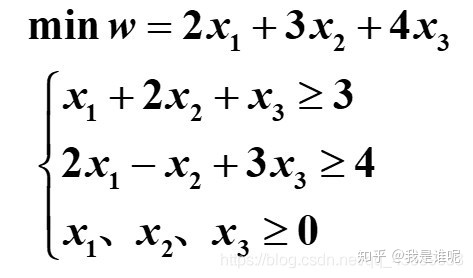
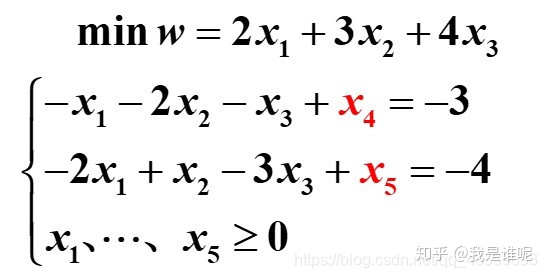
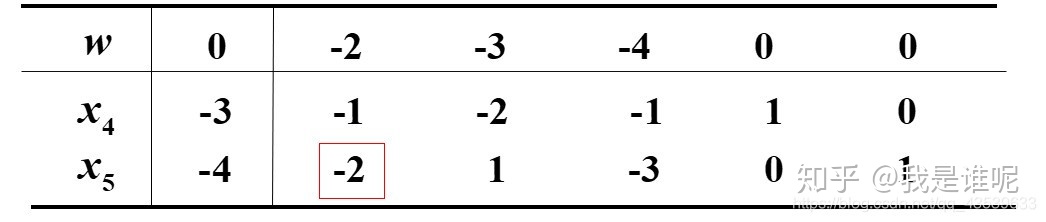
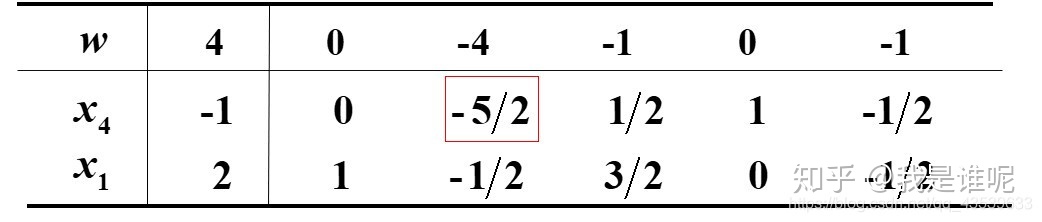
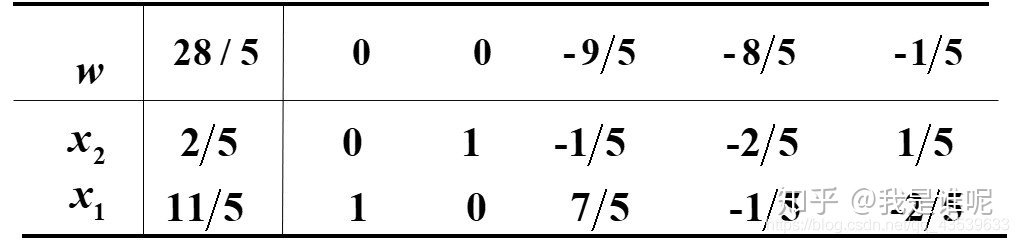
得原问题的最优解为 x1 = 11/5，x2 = 2/5，x3 = 0;最优值为 w = 28/5。
原创不易，你的鼓励是最大的支持。（约耗时1小时30分钟）
后续随着进一步学习还会出更多的运筹学文章，关注的话可以看到热乎乎的文章哦。
