我的公众号“每日晴天”，可关注领取我的笔记pdf版哦~

------------------------------------------------------------------------------

一、向量

1、简单的高中那些就不说了....

2、左右手系：

右手系：将右手四指（拇指除外）从x轴方向以小于π的角度弯向y轴方向，如果拇指所指的方向为z轴的方向，则称此坐标系为右手系。

左手系：将左手四指（拇指除外）从x轴方向以小于π的角度弯向y轴方向，如果拇指所指的方向为z轴的方向，则称此坐标系为左手系。

3、单位向量的方向：设向量

所以向量投影的定义为：

其中方向余弦是：

三个方向余弦的平方和等于1，

4、向量的内积：两个向量a和b的内积记作

其中：

5、对于任意的向量a，b，c，以及任意实数λ，有

（1）若

（2）

（3）

（4）

6、向量的外积：

（1）定义：两个向量a与b的外积记作

（2）性质：

①若a，b中有一个为0，则a×b=0。

②a×b=0的充分必要条件是a与b共线。

外积的几何意义：当a与b不平行时，

（3）外积的计算性质：对于任意的向量a，b，c，以及任意实数λ，外积有

①

④

（4）外积的计算：设

为了方便记忆可以写成：

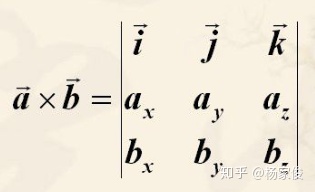
7、向量的混合积：

（1）定义：三个向量a，b，c的混合积记作(a,b,c)，它是一个数，规定

（2）几何意义：以三个非零向量a，b，c为棱作一个平行六面体，其底面积为|a×b|，高为

（3）在空间直角坐标系中建立混合积的坐标表达式：

设

从而有：

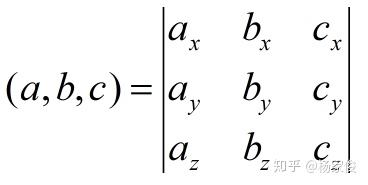
注意，有的地方是写成

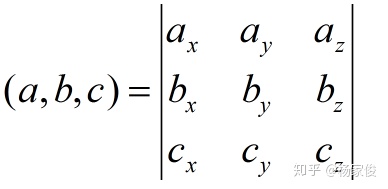
此时他们定义的混合积是：

二、空间平面及其方程

1、平面的点法式方程：设π平面的法向量

平面方程为：

（其实很简单，记住原理使法向量和平面上的一条向量垂直就可以了）

2、平面的一般式方程：

（1）设C≠0，则方程可以化成：

对照平面的点法式方程，我们可以知道这是一个过 以 法向量的平面。

（2）特点：

①D=0时，方程表示一个过原点的平面。

②当D≠0时，若A，B，C中只有一个为零，则平面平行于某个坐标轴

（如只有C=0时，平面的法向量与z轴垂直，因此平面平行于z轴）

③当D≠0时，若A，B，C中只有一个不为零，则平面平行于某坐标面

（如只有A≠0，则平面的法向量平行于x轴，因此平面平行于yOz面）

3、平面的截距式方程：当abc≠0时，平面

x、y、z轴上的截距分别为a、b、c，因此这种形式的平面称为平面的截距式方程。

4、平面的三点式方程：用三点可以确定一个平面，三个点都在这个平面上面，设

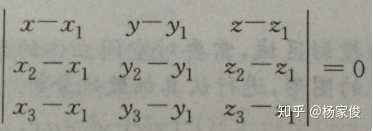
5、两平面间的关系设两个平面：

结论：

（1）两个平面重合

（2）两个平面平行

（3）两个平面相交

6、同轴平面束：经过同一条直线的所有平面的集合叫做同轴平面束。

设l为平面π1和平面π2的交线，则可以设λ1和λ2，就可以得到

以直线l为轴的平面束方程：

三、空间直线及其方程

1、直线的点向式方程（或者叫直线的对称式方程）：设

所以P(x,y,z)在l上

则有

2、直线的一般式方程：当

3、直线与直线的关系：设两条空间直线：

分析：l1过点

l2过点

两直线固定点的向量P1P2为：

（1）共面与异面的判断：s1、s2、P1P2的混合积为0则

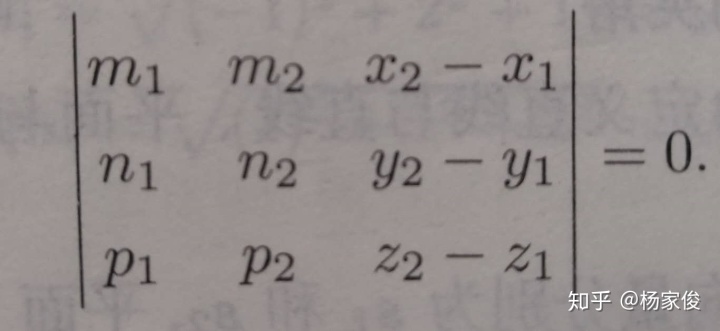
（2）共面后判断是否重合、平行、相交。

①两直线重合

②两直线平行

③两直线相交

四、直线与平面的关系，点和直线和平面的关系

1、直线与平面的关系：

设

记s为l的方向向量

（1）l在π上

垂直于n，且点 满足平面π的方程

（2）l与π平行

不满足平面π的方程

（3）l与π相交

不垂直

（4）l与π垂直

s×n=0）

2、直线与平面相互之间的夹角（都是锐角）

设l1、l2的方向向量分别为s1，s2。平面π1和π2的法向量分别为n1和n2。

（1）两条直线的夹角：s1和s2的夹角为θ，把

（2）两个平面的夹角：n1与n2的夹角是θ，把

（3）平面与直线的夹角：设s1和n1的夹角为θ，把

3、距离问题：

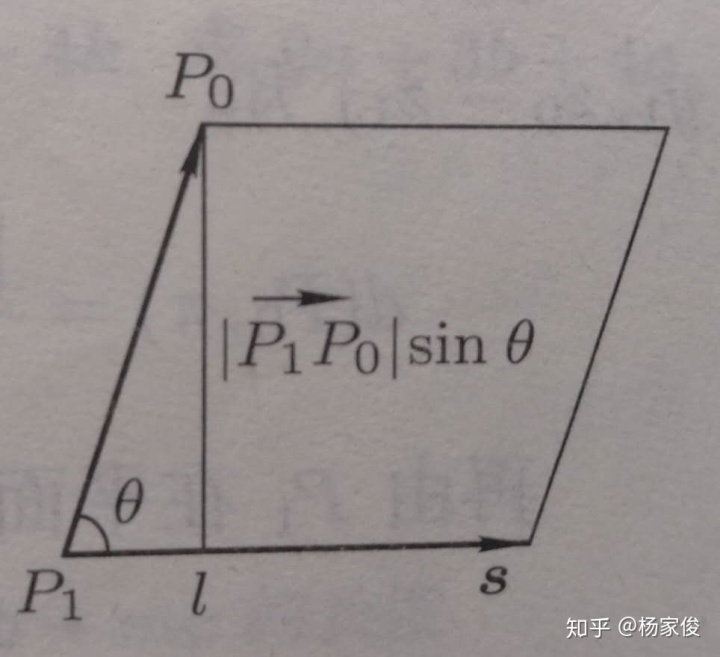
（1）点到直线的距离：设

设θ为向量s与向量P1P0的夹角，则从图中可以得到有

又因为从外积公式得到

所以

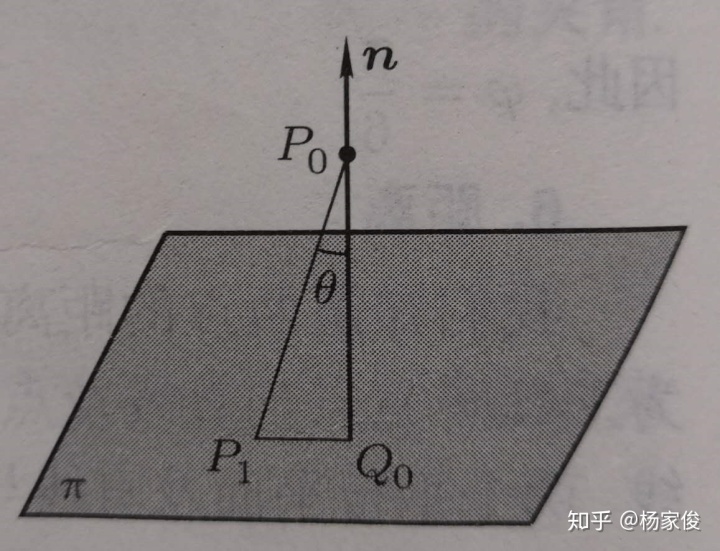
（2）点到平面的距离：设

设θ为向量n与向量P1P0的夹角，则从图中可以得到，

由内积公式可以得到

所以可以得到：

（对于π平面的方程为：Ax+By+Cz+D=0，

则公式为