【问题描述】[中等]

输入某二叉树的前序遍历和中序遍历的结果，请重建该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如，给出前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：3/ \9  20/  \15   7

【解答思路】

1. 递归解释1

关键要理解
前序遍历的左右子树根节点 可以根据中序遍历得到的左右子树的长度推断

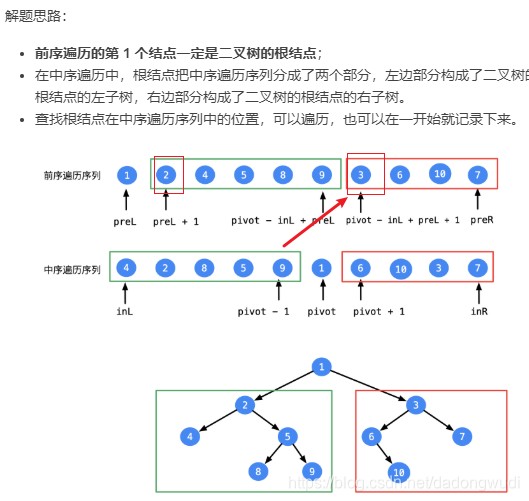
时间复杂度：O(N) 空间复杂度：O(N)

import java.util.HashMap;
import java.util.Map;class TreeNode {int val;TreeNode left;TreeNode right;TreeNode(int x) {val = x;}
}public class Solution {// 使用全局变量是为了让递归方法少传一些参数，不一定非要这么做private Map<Integer, Integer> reverses;private int[] preorder;public TreeNode buildTree(int[] preorder, int[] inorder) {int preLen = preorder.length;int inLen = inorder.length;// 可以不做判断，因为题目中给出的数据都是有效的if (preLen != inLen) {return null;}this.preorder = preorder;// 以空间换时间，否则，找根结点在中序遍历中的位置需要遍历reverses = new HashMap<>(inLen);for (int i = 0; i < inLen; i++) {reverses.put(inorder[i], i);}return buildTree(0, preLen - 1, 0, inLen - 1);}/*** 根据前序遍历数组的 [preL, preR] 和 中序遍历数组的 [inL, inR] 重新组建二叉树** @param preL 前序遍历数组的区间左端点* @param preR 前序遍历数组的区间右端点* @param inL  中序遍历数组的区间左端点* @param inR  中序遍历数组的区间右端点* @return 构建的新二叉树的根结点*/private TreeNode buildTree(int preL, int preR,int inL, int inR) {if (preL > preR || inL > inR) {return null;}// 构建的新二叉树的根结点一定是前序遍历数组的第 1 个元素int pivot = preorder[preL];TreeNode root = new TreeNode(pivot);int pivotIndex = reverses.get(pivot);// 这一步得画草稿，计算边界的取值，必要时需要解方程，并不难root.left = buildTree(preL + 1, preL + (pivotIndex - inL), inL, pivotIndex - 1);root.right = buildTree(preL + (pivotIndex - inL) + 1, preR, pivotIndex + 1, inR);return root;}
}

2. 递归解释2

时间复杂度：O(N) 空间复杂度：O(N)

    //利用原理,先序遍历的第一个节点就是根。在中序遍历中通过根 区分哪些是左子树的，哪些是右子树的//左右子树，递归HashMap<Integer, Integer> map = new HashMap<>();//标记中序遍历int[] preorder;//保留的先序遍历public TreeNode buildTree(int[] preorder, int[] inorder) {this.preorder = preorder;for (int i = 0; i < preorder.length; i++) {map.put(inorder[i], i);}return recursive(0,0,inorder.length-1);}/*** @param pre_root_idx  先序遍历的索引* @param in_left_idx  中序遍历的索引* @param in_right_idx 中序遍历的索引*/public TreeNode recursive(int pre_root_idx, int in_left_idx, int in_right_idx) {//相等就是自己if (in_left_idx > in_right_idx) {return null;}//root_idx是在先序里面的TreeNode root = new TreeNode(preorder[pre_root_idx]);// 有了先序的,再根据先序的，在中序中获 当前根的索引int idx = map.get(preorder[pre_root_idx]);//左子树的根节点就是 左子树的(前序遍历）第一个，就是+1,左边边界就是left，右边边界是中间区分的idx-1root.left = recursive(pre_root_idx + 1, in_left_idx, idx - 1);//由根节点在中序遍历的idx 区分成2段,idx 就是根//右子树的根，就是右子树（前序遍历）的第一个,就是当前根节点 加上左子树的数量// pre_root_idx 当前的根  左子树的长度 = 左子树的左边-右边 (idx-1 - in_left_idx +1) 。最后+1就是右子树的根了root.right = recursive(pre_root_idx + (idx-1 - in_left_idx +1)  + 1, idx + 1, in_right_idx);return root;}

【总结】

1.前中后序遍历变化的是[中]的位置，左到右的顺序不改变

• 前序遍历 中左右
• 中序遍历 左中右
• 后续遍历 左右中

2.前序+中序遍历可画出原二叉树

3. 多画图 写写写 遍历代码 手撕变量 大脑保持清醒

转载链接：https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/solution/mian-shi-ti-07-zhong-jian-er-cha-shu-di-gui-fa-qin/
来源：力扣（LeetCode）
转载链接：https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/solution/er-cha-shu-de-qian-xu-bian-li-fen-zhi-si-xiang-by-/
来源：力扣（LeetCode）