[剑指offer][JAVA]面试题第[10-1]题[斐波那契数列][动态规划][记忆化递归]

【问题描述】[中等]

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项。斐波那契数列的定义如下：F(0) = 0,   F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

【解答思路】

1. 动态规划

在这里插入图片描述

时间复杂度：O(N) 空间复杂度：O(1)

class Solution {public int fib(int n) {if(n == 0) return 0;int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for(int i = 2; i <= n; i++){dp[i] = dp[i-1] + dp[i-2];dp[i] %= 1000000007;}return dp[n];}
}

2. 动态规划空间复杂度优化

dp[n + 1] -> abc
在这里插入图片描述
时间复杂度：O(N) 空间复杂度：O(1)

public int fib(int n) {if(n==0 ){return 0;}if(n==1 ){return 1;}int a = 0;int b = 1;int c = 0;for(int i =2; i<=n;i++){c =(a +b)%1000000007;a = b ;b = c ;}return  c;}

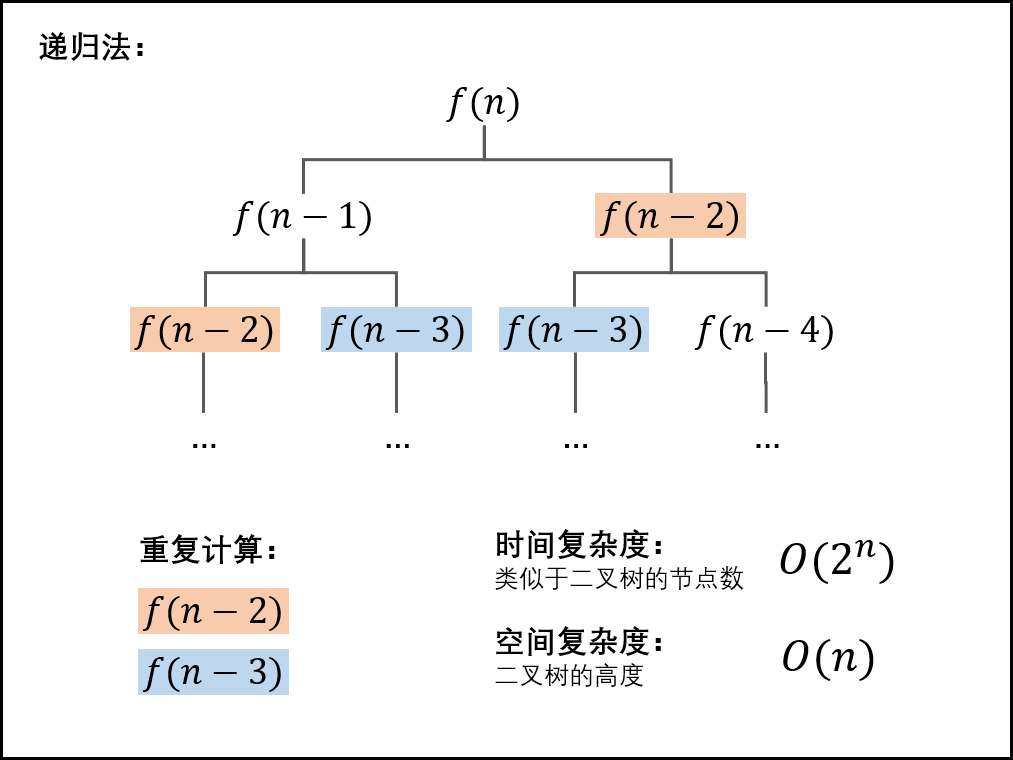
3. 递归（超时）

在这里插入图片描述
时间复杂度：O(2^N) 空间复杂度：O(1)

  public int fib(int n) {if(n==0) return 0;if(n==1) return 1;return (fib(n-1)+fib(n-2))%1000000007;}

4. 记忆化递归

在这里插入图片描述
时间复杂度：O(N) 空间复杂度：O(1)

class Solution {public int fib(int n) {if(n == 0) return 0;int[] memorization = new int[n+1]; //用于存储第0~n个数对应的值memorization[1] = 1; //第一二个数先定义好，由于第一个数是0，默认即可不用写出return Fibonacci(n,memorization);}public int Fibonacci(int n,int[] memo) {if(n < 2 ) //当n等于0或1时，将不再往下递归，直接返回记忆化结果对应的值return memo[n];if(memo[n] > 0) //当遇到之前计算过的数时，将不再递归往下找，直接用记忆化结果return memo[n];memo[n] = (Fibonacci(n - 2, memo) + Fibonacci(n - 1, memo)) % 1000000007;return memo[n];}
}