Discrete Cosine Transform，简写为DCT
函数的偶对称性使DCT只有实数域变换结果, 不再涉及复数运算，运算简单，费时少；

又保持了变换域的频率特性；

与人类视觉系统特性相适应；

得到了更加广泛的应用。

 二维偶DCT(2D-DCT)

基本思想：

把一个的图像数据矩阵延拓成二维平面上的偶对称 阵列。延拓方式有两种：

（1）围绕图像边缘（但不重叠）将其折叠成对称形式而 得到的变换称为偶离散余弦变换；

（2）通过重叠图像的第一列像素和第行像素将其 折叠成对称形式而得到的变换称为奇离散余弦变换。

下面只介绍偶离散余弦变换。

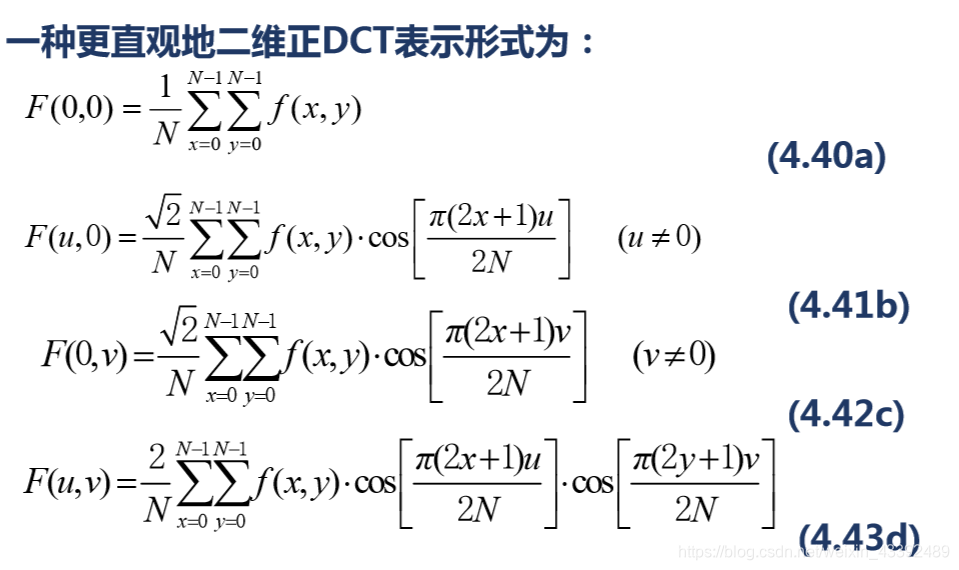
DCT变换的基函数与基图像

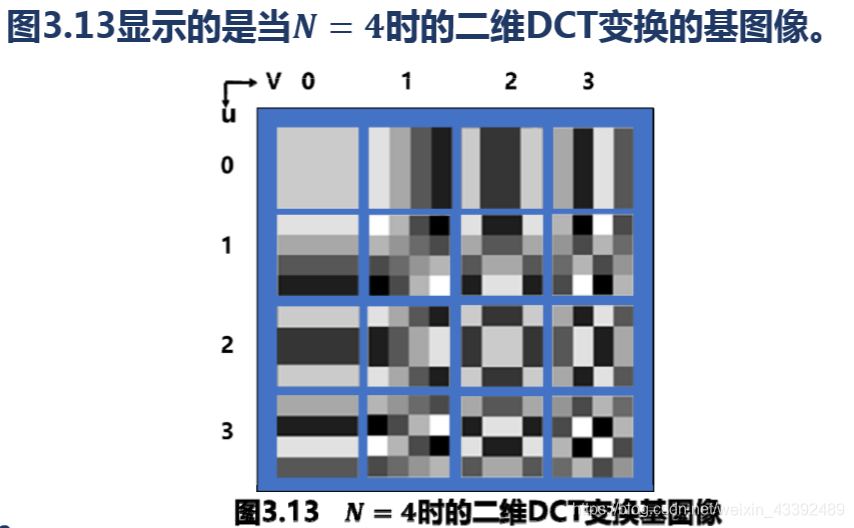
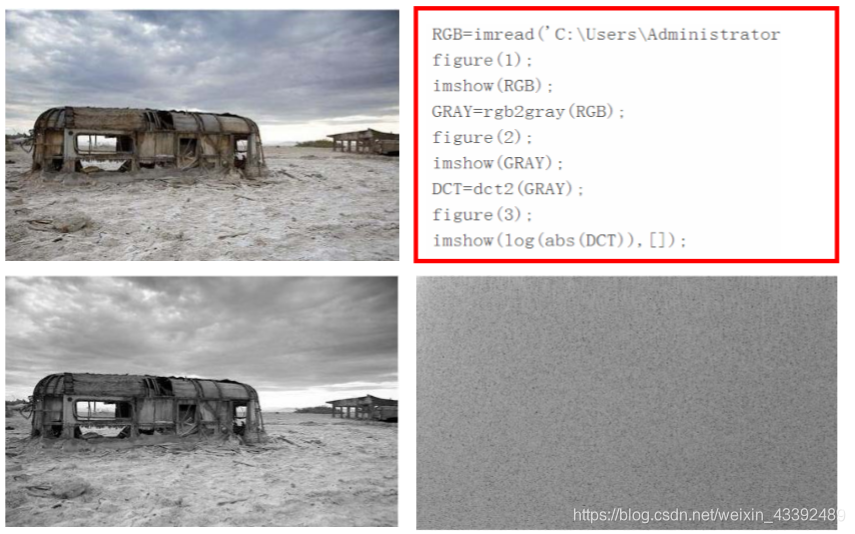
 DCT变换的实例