【问题描述】[中等]

【解答思路】

1. 动态规划思路一 自上而下

第 1 步：设计状态
f[i][j] 表示从三角形顶部走到位置 (i,j) 的最小路径和
位置(i,j) 指的是三角形中第 i 行第 j 列（均从 00 开始编号）的位置
第 2 步：状态转移方程

第 3 步：考虑初始化
f[0][0]=c[0][0]
第 4 步：考虑输出
f[n−1][0] 到 f[n-1][n-1] 中的最大值，其中 n 是三角形的行数
第 5 步：考虑是否可以状态压缩
是
时间复杂度：O(N^2) 空间复杂度：O(N^2)

class Solution {public int minimumTotal(List<List<Integer>> triangle) {int n = triangle.size();int[][] f = new int[n][n];f[0][0] = triangle.get(0).get(0);for (int i = 1; i < n; ++i) {f[i][0] = f[i - 1][0] + triangle.get(i).get(0);for (int j = 1; j < i; ++j) {f[i][j] = Math.min(f[i - 1][j - 1], f[i - 1][j]) + triangle.get(i).get(j);}f[i][i] = f[i - 1][i - 1] + triangle.get(i).get(i);}int minTotal = f[n - 1][0];for (int i = 1; i < n; ++i) {minTotal = Math.min(minTotal, f[n - 1][i]);}return minTotal;}
}

动态规划 + 空间优化

时间复杂度：O(N^2) 空间复杂度：O(2N)

class Solution {public int minimumTotal(List<List<Integer>> triangle) {int n = triangle.size();int[][] f = new int[2][n];f[0][0] = triangle.get(0).get(0);for (int i = 1; i < n; ++i) {int curr = i % 2;int prev = 1 - curr;f[curr][0] = f[prev][0] + triangle.get(i).get(0);for (int j = 1; j < i; ++j) {f[curr][j] = Math.min(f[prev][j - 1], f[prev][j]) + triangle.get(i).get(j);}f[curr][i] = f[prev][i - 1] + triangle.get(i).get(i);}int minTotal = f[(n - 1) % 2][0];for (int i = 1; i < n; ++i) {minTotal = Math.min(minTotal, f[(n - 1) % 2][i]);}return minTotal;}
}

时间复杂度：O(N^2) 空间复杂度：O(N)

class Solution {public int minimumTotal(List<List<Integer>> triangle) {int n = triangle.size();int[] f = new int[n];f[0] = triangle.get(0).get(0);for (int i = 1; i < n; ++i) {f[i] = f[i - 1] + triangle.get(i).get(i);for (int j = i - 1; j > 0; --j) {f[j] = Math.min(f[j - 1], f[j]) + triangle.get(i).get(j);}f[0] += triangle.get(i).get(0);}int minTotal = f[0];for (int i = 1; i < n; ++i) {minTotal = Math.min(minTotal, f[i]);}return minTotal;}
}

2. 动态规划 自底向上 （考虑边界减少）

第 1 步：设计状态
dp[i][j] 表示从点 (i, j)(i,j) 到底边的最小路径和。
第 2 步：状态转移方程
dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle[i][j]
第 3 步：考虑初始化
dp[i][j] 均为’0’
第 4 步：考虑输出
dp[0][0]
第 5 步：考虑是否可以状态压缩
是
时间复杂度：O(N^2) 空间复杂度：O(N^2)

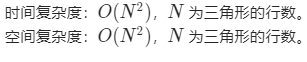
class Solution {public int minimumTotal(List<List<Integer>> triangle) {int n = triangle.size();// dp[i][j] 表示从点 (i, j) 到底边的最小路径和。int[][] dp = new int[n + 1][n + 1];// 从三角形的最后一行开始递推。for (int i = n - 1; i >= 0; i--) {for (int j = 0; j <= i; j++) {dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle.get(i).get(j);}}return dp[0][0];}
}
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200714110356304.png)

时间复杂度：O(N^2) 空间复杂度：O(N)

class Solution {public int minimumTotal(List<List<Integer>> triangle) {int n = triangle.size();int[] dp = new int[n + 1];for (int i = n - 1; i >= 0; i--) {for (int j = 0; j <= i; j++) {dp[j] = Math.min(dp[j], dp[j + 1]) + triangle.get(i).get(j);}}return dp[0];}
}

3. 递归

暴力搜索会有大量的重复计算，导致 超时，因此在 结合记忆化数组进行优化。

class Solution {public int minimumTotal(List<List<Integer>> triangle) {return  dfs(triangle, 0, 0);}private int dfs(List<List<Integer>> triangle, int i, int j) {if (i == triangle.size()) {return 0;}return Math.min(dfs(triangle, i + 1, j), dfs(triangle, i + 1, j + 1)) + triangle.get(i).get(j);}
}

递归 + 记忆化
时间复杂度：O(N^2) 空间复杂度：O(N^2)

class Solution {Integer[][] memo;public int minimumTotal(List<List<Integer>> triangle) {memo = new Integer[triangle.size()][triangle.size()];return  dfs(triangle, 0, 0);}private int dfs(List<List<Integer>> triangle, int i, int j) {if (i == triangle.size()) {return 0;}if (memo[i][j] != null) {return memo[i][j];}return memo[i][j] = Math.min(dfs(triangle, i + 1, j), dfs(triangle, i + 1, j + 1)) + triangle.get(i).get(j);}
}

【总结】

1.动态规划流程

第 1 步：设计状态
第 2 步：状态转移方程
第 3 步：考虑初始化
第 4 步：考虑输出
第 5 步：考虑是否可以状态压缩

2.自下而上 自上而下均可以实现 哪个顺手使用哪个 哪个边界清晰用哪个

转载链接：https://leetcode-cn.com/problems/triangle/solution/san-jiao-xing-zui-xiao-lu-jing-he-by-leetcode-solu/
转载链接：https://leetcode-cn.com/problems/triangle/solution/di-gui-ji-yi-hua-dp-bi-xu-miao-dong-by-sweetiee/