【问题描述】[中等]

【解答思路】

1. 拓扑排序

复杂度分析

HashSet[] 数组

import java.util.HashSet;
import java.util.LinkedList;
import java.util.Queue;public class Solution {public boolean canFinish(int numCourses, int[][] prerequisites) {if (numCourses <= 0) {return false;}// 特判int pLen = prerequisites.length;if (pLen == 0) {return true;}int[] inDegree = new int[numCourses];HashSet<Integer>[] adj = new HashSet[numCourses];for (int i = 0; i < numCourses; i++) {adj[i] = new HashSet<>();}for (int[] p : prerequisites) {inDegree[p[0]]++;adj[p[1]].add(p[0]);}Queue<Integer> queue = new LinkedList<>();// 首先加入入度为 0 的结点for (int i = 0; i < numCourses; i++) {if (inDegree[i] == 0) {queue.add(i);}}// 记录已经出队的课程数量int cnt = 0;while (!queue.isEmpty()) {Integer top = queue.poll();cnt += 1;// 遍历当前出队结点的所有后继结点for (int successor : adj[top]) {inDegree[successor]--;if (inDegree[successor] == 0) {queue.add(successor);}}}return cnt == numCourses;}
}

List<List>

class Solution {public boolean canFinish(int numCourses, int[][] prerequisites) {int[] indegrees = new int[numCourses];List<List<Integer>> adjacency = new ArrayList<>();Queue<Integer> queue = new LinkedList<>();for(int i = 0; i < numCourses; i++)adjacency.add(new ArrayList<>());// Get the indegree and adjacency of every course.for(int[] cp : prerequisites) {indegrees[cp[0]]++;adjacency.get(cp[1]).add(cp[0]);}// Get all the courses with the indegree of 0.for(int i = 0; i < numCourses; i++)if(indegrees[i] == 0) queue.add(i);// BFS TopSort.while(!queue.isEmpty()) {int pre = queue.poll();numCourses--;for(int cur : adjacency.get(pre))if(--indegrees[cur] == 0) queue.add(cur);}return numCourses == 0;}
}

2. DFS

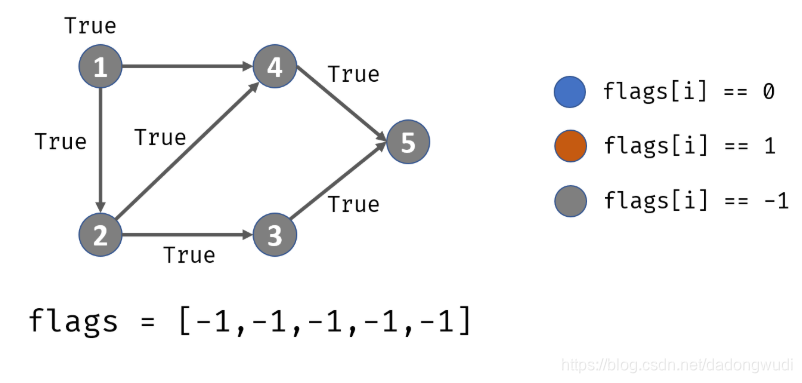
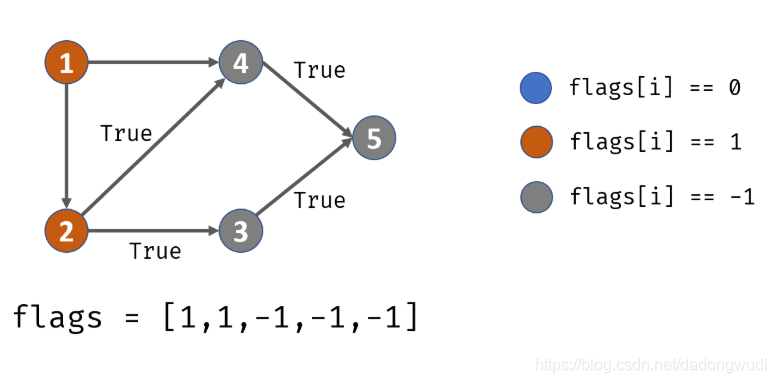
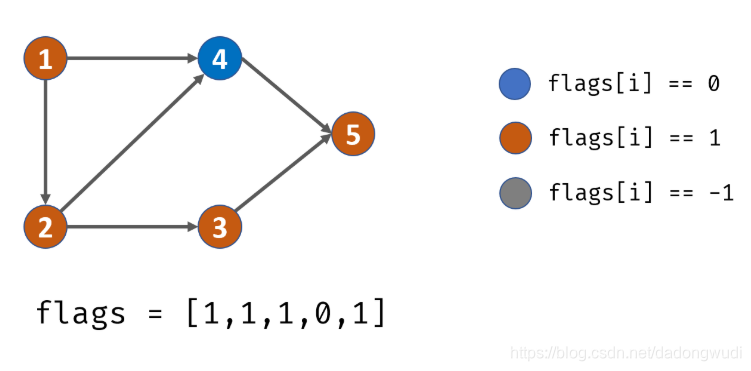
复杂度

class Solution {public boolean canFinish(int numCourses, int[][] prerequisites) {List<List<Integer>> adjacency = new ArrayList<>();for(int i = 0; i < numCourses; i++)adjacency.add(new ArrayList<>());int[] flags = new int[numCourses];for(int[] cp : prerequisites)adjacency.get(cp[1]).add(cp[0]);for(int i = 0; i < numCourses; i++)if(!dfs(adjacency, flags, i)) return false;return true;}private boolean dfs(List<List<Integer>> adjacency, int[] flags, int i) {if(flags[i] == 1) return false;if(flags[i] == -1) return true;flags[i] = 1;for(Integer j : adjacency.get(i))if(!dfs(adjacency, flags, j)) return false;flags[i] = -1;return true;}
}

【总结】

1. 拓扑排序

拓扑排序实际上应用的是贪心算法。贪心算法简而言之：每一步最优，全局就最优。

具体到拓扑排序，每一次都从图中删除没有前驱的顶点，这里并不需要真正的做删除操作，我们可以设置一个入度数组，每一轮都输出入度为 00 的结点，并移除它、修改它指向的结点的入度（-1−1即可），依次得到的结点序列就是拓扑排序的结点序列。如果图中还有结点没有被移除，则说明“不能完成所有课程的学习”。

拓扑排序保证了每个活动（在这题中是“课程”）的所有前驱活动都排在该活动的前面，并且可以完成所有活动。拓扑排序的结果不唯一。拓扑排序还可以用于检测一个有向图是否有环。相关的概念还有 AOV 网，这里就不展开了。

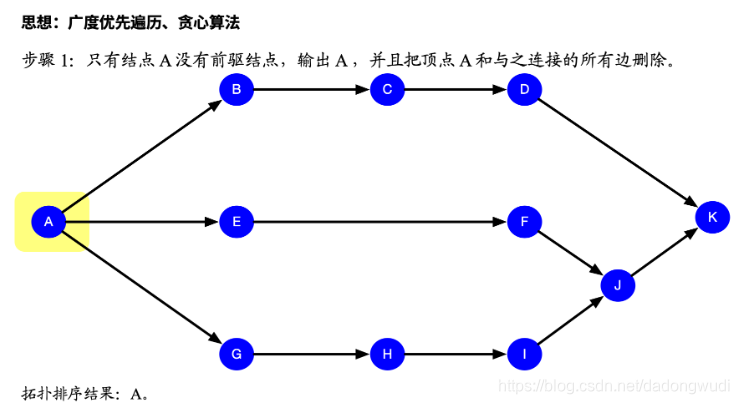
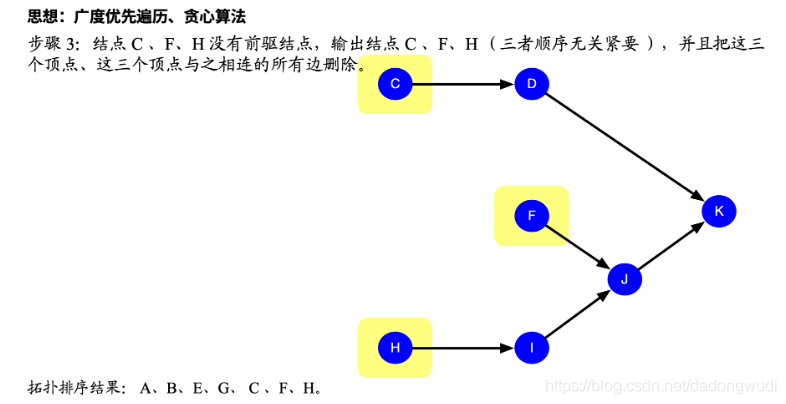
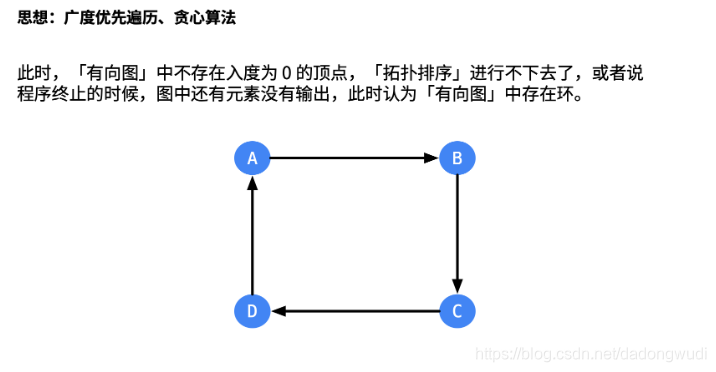
2.拓扑排序

1.统计箭头指向的度
2.度为0的入队
3.统计层数 出队 相关度减一且度为0入队
4.队为空作判断

3.相关题目[Leedcode][JAVA][第210 题][课程表 II][拓扑排序][BFS][DFS][有向图]

转载链接：https://leetcode-cn.com/problems/course-schedule/solution/tuo-bu-pai-xu-by-liweiwei1419/
作者：Krahets
转载链接：https://leetcode-cn.com/problems/course-schedule/solution/course-schedule-tuo-bu-pai-xu-bfsdfsliang-chong-fa/