【问题描述】[简单]

【解答思路】

1. 递归

终止条件/基本情况 root ==null
递推关系 max(l,r)+1

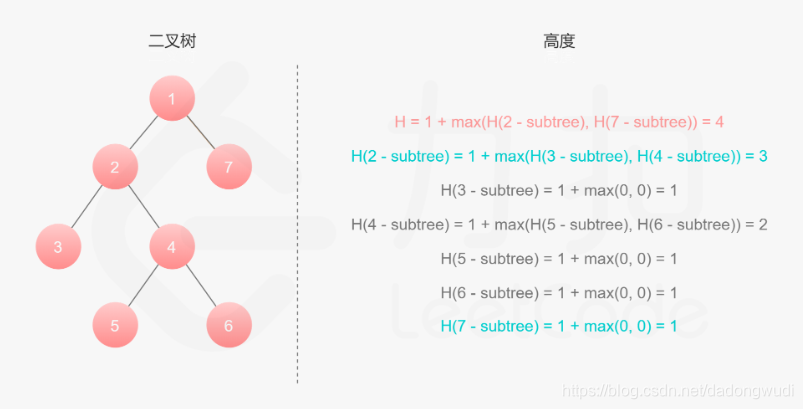
时间复杂度：O(N) 空间复杂度：O(height)

class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;} else {int leftHeight = maxDepth(root.left);int rightHeight = maxDepth(root.right);return Math.max(leftHeight, rightHeight) + 1;}}
}

2. 广度优先搜索 BFS

主要思路：

1. 初始化 root入队 ，ans记录层数，root不为空，层数为1
2. 出队前记录当前队列大小size（当前层含有元素个数）
3. 根据获得size依次出队 如果左右节点不为空 加入队列（组成下一层的元素）
4. 根据size遍历完毕后，当前层遍历完毕，层数+1
   时间复杂度：O(N) 空间复杂度：O(1)

class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}Queue<TreeNode> queue = new LinkedList<TreeNode>();queue.offer(root);int ans = 0;while (!queue.isEmpty()) {int size = queue.size();while (size > 0) {TreeNode node = queue.poll();if (node.left != null) {queue.offer(node.left);}if (node.right != null) {queue.offer(node.right);}size--;}ans++;}return ans;}
}

【总结】

1.二叉树 递归 BFS DFS

2.递归

在实现递归函数之前，有两件重要的事情需要弄清楚:

递推关系：一个问题的结果与其子问题的结果之间的关系。
基本情况：不需要进一步的递归调用就可以直接计算答案的情况。可理解为递归跳出条件。
一旦我们计算出以上两个元素，再想要实现一个递归函数，就只需要根据递推关系调用函数本身，直到其抵达基本情况。

3.递归模板套路

由下到上

有上到下

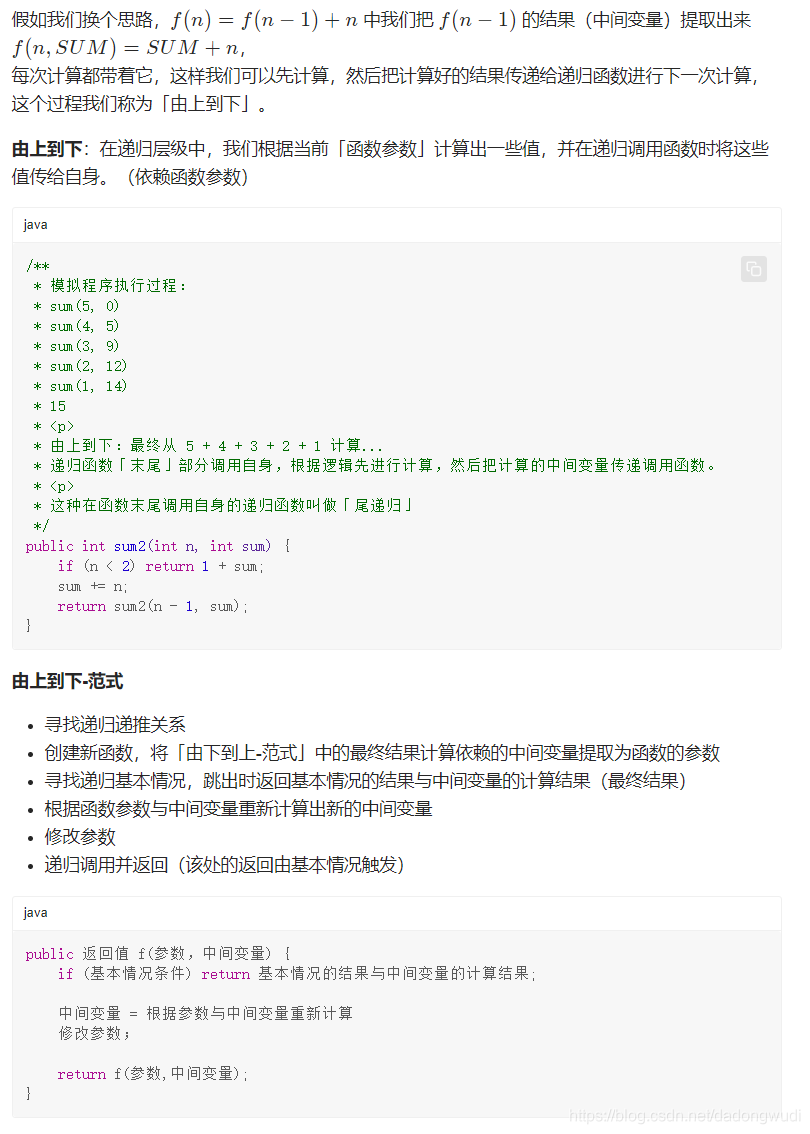
区别

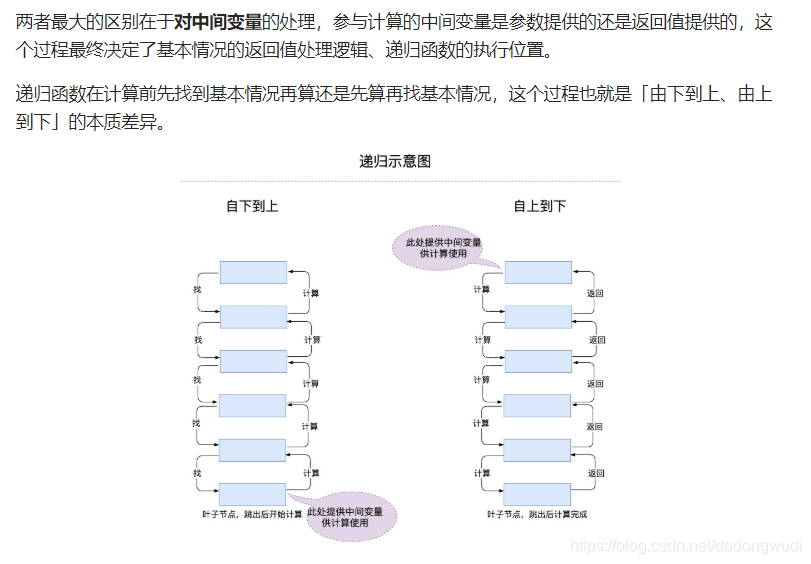
4.相关题目

[Leetcode][第111题][JAVA][BFS][二叉树的最小深度][BFS][递归]

参考链接：https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/solution/er-cha-shu-de-zui-da-shen-du-by-leetcode-solution/
递归学习资料：https://leetcode-cn.com/circle/article/koSrVI/