1. 递归的定义

编程语言中，函数 Func(Type a,……) 直接或间接调用函数本身，则该函数称为「递归函数」。

在实现递归函数之前，有两件重要的事情需要弄清楚:

• 递推关系：一个问题的结果与其子问题的结果之间的关系。
• 基本情况：不需要进一步的递归调用就可以直接计算答案的情况。可理解为递归跳出条件。

一旦我们计算出以上两个元素，再想要实现一个递归函数，就只需要根据递推关系调用函数本身，直到其抵达基本情况。

递归函数的编写看起来比较难，其实是有套路可寻的，本文在力扣刷题阶段总结了写递归的一些范式技巧并在后续实战中进行验证，深入理解其中思维过程再去刷题时感觉轻而易举了。

1.1 递推关系

下面的插图给出了一个 5 行的帕斯卡三角，根据上面的定义，我们生成一个具有确定行数的帕斯卡三角形。

首先，我们定义一个函数 f(i,j)，它将会返回帕斯卡三角形第 i 行、第 j列的数字。可以看到，每行的最左边和最右边的数字是基本情况，它总是等于 11。
每个数是它左上方和右上方的数的和。

• 递推关系：f(i,j)=f(i−1,j−1)+f(i−1,j)
• 基本情况：f(i,j)=1f(i,j)=1 ，当 j=1j=1 或者 i=ji=j 时。
  再看一个「二叉树的最大深度」递推关系推导的案例：

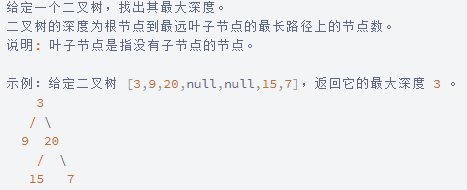
二话不多，先定义一个 f(node)，寻找当前节点 node 与当前节点子节点的关系，子节点可能是左、可能是右。

所以有子节点有 f(node.left)、f(node.right) 两种情况，然后寻找 f(node)与它们的关系。当前节点的最大深度 = 他子节点的最大深度 + 1。

• 递推关系：f(node)=Max(f(node.left),f(node.right))+1

• 基本情况：当前节点不存在时，高度为 0

对于二叉树的算法题，我们会推导递推关系时，所有相关的算法一下就变得很容易。但是有了递推关系后如何写出递归函数来呢？
介于最近对算法的研究，发现大部分所谓的动态规划、回溯其实都是写递归函数的一些思维过程。本文总结了写递归的范式。有了这些范式，我们直接拿着题目套入就很容易写出一个通过率很高的函数。

1.2 尾递归

尾递归：尾递归函数是递归函数的一种，其中递归调用是递归函数中的最后一条指令。并且在函数中应该只有一次递归调用。

尾递归的好处是，它可以避免递归调用期间栈空间开销的累积，因为系统可以为每个递归调用重用栈中的固定空间。形象的理解参考 2.2.3 节内容中关于自顶向下的示例图。

2. 写递归函数的招式

下面我们以累加的示例说明写递归的思路。

1+2+3+4+…+n，函数表达式为 f(n)=f(n−1)+n

2.1 寻找基本情况

累加示例中，基本情况为 n=1 时，f(1)=1。

你也可以设定为 f(2)=1+2=3，只要能正确跳出递归即可。

2.2 寻找递推关系（难点）

累加示例中，递推关系为 f(n)=f(n−1)+n，f(n) 每次计算时依赖 f(n−1) 的结果，所以我们把 f(n−1)的结果看作是中间变量。

中间变量其实就是联系递归函数的纽带，分析出中间变量递归函数也就实现了 80%。

大白话：当前结果必须借助前一个结果，前一个借助前前一个… 一直到时我们找到了「基本情况」。
然后拿到「基本情况」开始往回计算。这个过程我们简称为「自底向上」。

下面我们用 f(5)=1+2+3+4+5=15 这个过程进行分析。

2.2.1 自底向上

自底向上：在每个递归层次上，我们首先递归地调用自身，然后根据返回值进行计算。（依赖返回值）

大白话：将问题细化分解，例如计算 1-n 的和，可以逐步分解为 f(n) = f(n-1) + n

/** * 模拟程序执行过程：* 5 + sum(4)* 5 + (4 + sum(3)* 5 + 4 + (3 + sum(2))* 5 + 4 + 3 + (2 + sum(1))* ------------------> 到达基本情况 sum(1) = 1 ，开始执行 ③ 行代码* 5 + 4 + 3 + (2 + 1)* 5 + 4 + (3 + 3)* 5 + (4 + 6)* (5 + 10)* 15* <p>* 自底向上：最终从 1 + 2 + 3 + 4 + 5 计算...* 递归函数「开始」部分调用自身，这个过程就是找到基本情况），然后根据返回值进行计算。*/
public int sum(int n) {if (n < 2) return n;       // ① 递归基本情况int childSum = sum(n - 1); // ② 寻找基本情况return n + childSum;       // ③ 根据返回值运算
}

自底向上的过程其实是一个先寻找基本情况（跳出条件），然后根据基本情况计算它的父问题，一直到最后一个父问题计算后，返回最终结果。

本示例中基本情况是 sum(1) = 1，基本情况的父问题是 sum(2) = 2 + sum(1)。即从 N 加到 1，到达 1 时触发结果开始逐个返回子问题的结果。

自底向上-范式

• 寻找递归递推关系
• 寻找递归基本情况，跳出时返回基本情况的结果
• 修改递归函数的参数
• 递归调用并返回中间变量
• 使用递归函数的返回值与当前参数进行计算，并返回最终结果

public 返回值 f(参数) {if (基本情况条件) return 基本情况的结果;       修改参数；返回值 = f(参数); 最终结果 = 根据参数与返回值计算return 最终结果;
}

2.2.2 自顶向下

假如我们换个思路，f(n)=f(n−1)+n 中我们把 f(n−1) 的结果（中间变量）提取出来 f(n,SUM)=SUM+n，
每次计算都带着它，这样我们可以先计算，然后把计算好的结果传递给递归函数进行下一次计算，这个过程我们称为「自顶向下」。

自顶向下：在递归层级中，我们根据当前「函数参数」计算出一些值，并在递归调用函数时将这些值传给自身。（依赖函数参数）

大白话：从最子问题逐步计算出最终问题，例如计算 1-n 的和，可以逐步分解为 n + sum(n-1) = sum(n)，即从 1 加到 N。

/*** 模拟程序执行过程：* sum(5, 0)* sum(4, 5)* sum(3, 9)* sum(2, 12)* sum(1, 14)* 15* <p>* 自顶向下：最终从 5 + 4 + 3 + 2 + 1 计算...* 递归函数「末尾」部分调用自身，根据逻辑先进行计算，然后把计算的中间变量传递调用函数。* <p>* 这种在函数末尾调用自身的递归函数叫做「尾递归」*/
public int sum2(int n, int sum) {if (n < 2) return 1 + sum;sum += n;return sum2(n - 1, sum);
}

自顶向下-范式

• 寻找递归递推关系
• 创建新函数，将「自底向上-范式」中的最终结果计算依赖的中间变量提取为函数的参数
• 寻找递归基本情况，跳出时返回基本情况的结果与中间变量的计算结果（最终结果）
• 根据函数参数与中间变量重新计算出新的中间变量
• 修改参数
• 递归调用并返回（该处的返回由基本情况触发）

public 返回值 f(参数，中间变量) {if (基本情况条件) return 基本情况的结果与中间变量的计算结果;中间变量 = 根据参数与中间变量重新计算修改参数；return f(参数,中间变量);
}

2.2.3 自底向上、自顶向下的区别

两者最大的区别在于对中间变量的处理，参与计算的中间变量是参数提供的还是返回值提供的，这个过程最终决定了基本情况的返回值处理逻辑、递归函数的执行位置。

递归函数在计算前先找到基本情况再算还是先算再找基本情况，这个过程也就是「自底向上、自顶向下」的本质差异。

2.3 优化递归函数

优化点总结为：

• 充分分析基本情况（跳出条件），避免临界值跳不出递归，导致栈溢出。

• 分析递归深度，太深的递归容易导致栈溢出。

• 分析是否有重复计算问题，主要分析函数参数值是否会出现重复，直接代入递归的递推关系中运算即可。如果会出现重复使用数据结构记录（记忆化消除重复）。

比如：斐波那契数列 f(n)=f(n−1)+f(n−2)，如果直接采用该公式进行递归会重复计算很多表达式。

• 分析数据溢出问题

• 因为递归会对栈及中间变量的状态保存有额外的开销，将「自底向上」优化为「自顶向下」，再改写为尾递归，再退化为循环结构。

尾递归是我们可以实现的递归的一种特殊形式。与记忆化技术不同的是，尾递归通过消除递归带来的堆栈开销，优化了算法的空间复杂度。更重要的是，有了尾递归，就可以避免经常伴随一般递归而来的堆栈溢出问题，而尾递归的另一个优点是，与非尾递归相比，尾部递归更容易阅读和理解。这是由于尾递归不存在调用后依赖（即递归调用是函数中的最后一个动作），这一点不同于非尾递归，因此，只要有可能，就应该尽量运用尾递归。

2.4 改为循环

递归本身的风险比较高，实际项目不推荐采用。部分编程语言可以对尾递归进行编译优化（优化为循环结构），比如 Scala 语言。但是部分语言不支持，比如 Java。

函数式编程时推荐尾递归写法并加标识让编译器进行优化，下面是 Scala 语言优化的一个案例：

// Scala 编译前的尾递归写法，并注解为尾递归
@scala.annotation.tailrec
def sum2(n: Int, sum: Int): Int = {if (n < 2) return sum + nsum2(n - 1, sum + n)
}// 编译后优化为循环结果
public int sum2(int n, int sum) {while (true) {if (n < 2) return sum + n; sum += n;n--;} 
}

一个不是尾递归的案例：

// 并不是最后一行递归调用就是尾递归，下面例子其实是一个自底向上的递归写法，返回值与 n 有关。
def sum(n: Int): Int = {if (n < 2) return nreturn n + sum(n - 1) 
}

3. 案例实战-递归乘法

对于有些算法，递归比循环实现简单，比如二叉树的前中后序遍历。但是大部分时候循环比递归更直观更容易理解。

下面我们以力扣一个算法题 递归乘法 进行实战，实战前请花 10 min 时间尝试自我完成。

如果只是局限于看小说似的阅读，现在就可以「ALT+F4」了。 🙈

递归乘法。 写一个递归函数，不使用 * 运算符， 实现两个正整数的相乘。
可以使用加号、减号、位移，但要吝啬一些。

3.1 审题思路

乘法本身是加法的变种，A * B = A 个 B 相加。

寻找基本情况的条件为：A 个 B 相加一次 A - 1，A 如果为 1 时即找到最后一个 B 。

首先我们用循环完成。

public int multiplyFor(int A, int B) {int sum = 0;while (A-- > 0) sum += B;return sum;
}

3.2 尝试递归

寻找递推关系 f(a,b)=b+f(a−1,b)，基本情况条件为 a<2a<2 时表示找到最后一个 bb

套入「自底向上」的范式如下：

- 寻找递归递推关系
- 寻找递归基本情况，跳出时返回基本情况的结果 -> B
- 修改递归函数的参数，递归调用并返回中间变量 -> return sum（中间变量）
- 使用递归函数的返回值进行计算并返回最终结果 -> sum + Bpublic int multiply(int A, int B) {if (A < 2) return B;          // 跳出时返回基本情况的结果int sum = multiply(A - 1, B); // 先递归return sum + B;               // 再计算，依赖递归的返回值
}

尝试转换为递归「自顶向下」（尾递归），依赖中间结果（每次的和），先计算再递归。

f(a,b)=sum+f(a−n,b)，sum为已经计算了的 n 个 b 的和。

- 寻找递推关系
- 创建新函数，将「自底向上-范式」中的最终结果计算依赖的中间变量提取为函数的参数 -> multiply1Help 函数 sum 为中间变量
- 寻找递归基本情况，跳出时返回基本情况的结果与中间变量的计算结果（最终结果） -> return B + sum
- 根据函数参数与中间变量重新计算出新的中间变量 -> sum += B
- 修改参数 -> A - 1
- 递归调用并返回（该处的返回由基本情况条件触发）-> B + sumpublic int multiply1(int A, int B) {return multiply1Help(A, B, 0);
}public int multiply1Help(int A, int B, int sum) {if (A < 2) return B + sum;          // 跳出时返回基本情况的结果与中间变量的计算结果sum += B;                           // 根据函数参数与中间变量重新计算出新的中间变量return multiply1Help(A - 1, B, sum);// 由基本情况条件触发决定，最终返回 B + sum
}

至此，两个递归写法已实现，实际编码中「自顶向下」比「自底向上」更容易理解，因为我们的思维从上向下思考容易，但是逆着思考就比较抽象了。
这个抽象过程需要大量的练习，末尾推荐了部分递归的算法题。

3.3 尝试优化

分析上述实现的两个递归时间复杂度为 O(n)O(n)，n=Max(A,B)，考虑如何优化时间复杂度。

• 如果 A > B ，处理 A 次，因此考虑使用 M=MIN(A,B)M=MIN(A,B) 作为循环次数。比如 100∗1100∗1 时可优化 100 倍
• 分析重复计算问题，目前没有。
• 分析参数的边界问题，目前没有。题目给定约束都是正整数。
• 优化时间复杂度，重新分析递推关系为 a∗b=(a/2)∗(b∗2)，直到 a/2a/2 等于 1 时，b 就是最终结果，我们基于二进制的位移操作进行优化，
  但是要考虑如果是奇数除以 2 时会丢失一个 b，这样复杂度优化为 O(log₂n)
  ​

优化过程示例：a * b = (a/2) * (b*2)偶数为循环次数的运算过程
8 * 9 
4 * 18
2 * 36
1 * 72
72奇数为循环次数的运算过程
7 * 9
9 + (3 * 18)        -> 7/2 时丢失一个 9 
9 + 18 + (1 * 36)   -> 3/2 时丢失一个 18 
9 + 18 + 36 
63

将上述过程转换为「自顶向下」尾递归代码实现（你可以尝试「自底向上」实现，可以套入范式进行验证）：

public int multiply2(int A, int B) {return (A < B) ? multiply2Help(A, B, 0) : multiply2Help(B, A, 0); // 寻找最小循序次数
}// missPart 为奇数除以 2 时丢失的部分
public int multiply2Help(int A, int B, int missPart) {if (A < 2) return missPart + B;   // 最终结果 = 丢失的部分 + 最终 B 的结果missPart += (A & 1) == 1 ? B : 0; // 是否为奇数，奇数时记录丢失的部分return multiply2Help(A >> 1, B << 1, missPart); // 位移运算优化
}

4. 案例实战-青蛙跳台阶

一只青蛙一次可以跳上 1 级台阶，也可以跳上 2 级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。 n = 0 时忽略。

1. 寻找基本情况：剩余一个台阶时只能有一种跳法 f(1)=1，剩余两个台阶时只能有两种跳法 f(2)=2，或者剩余 3 个台阶时有 3 种跳法（1-1-1、1-2、2-1）

2. 寻找递推关系：如果跳 1 级台阶就少一个，结果为 f(n−1) 种，如果跳 2 级台阶就少 2 个，结果为 f(n−2)种。
   所以推导递推关系为 f(n)=f(n−1)+f(n−2)

3. 优化递归：考虑重复计算问题，因为递推关系中 n 涉及减法运算，肯定会出现重复代入 f(n) 计算，因此考虑使用数据结构保存计算过的结果。分析数据溢出问题，如果没有给定约束条件，要考虑返回跳法是否会溢出。

自底向上的范式套入实现：

/*** - 寻找递推关系 f(n)=f(n-1)+f(n-2)* - 寻找递归基本情况，跳出时返回基本情况的结果 f(1) = 1,f(2) = 2* - 修改递归函数的参数，递归调用 -> 套入递推关系，当前 n 台阶跳法为 count=f(n-1)+f(n-2)* - 使用递归函数的返回值进行计算并返回最终结果 -> 递归返回跳法数 count 即为最终结果 */
public int numWays1(int n) {if (n == 1) return 1;if (n == 2) return 2;int count = numWays1(n - 1) + numWays1(n - 2);return count;
}// 优化上述初步完成的递归思路：
// 2 个 if 可有优化 为 if (n <= 2) return n; 减少执行次数
// 递归函数重复计算问题，使用临时变量保存private final Map<Integer, Integer> statusRecord = new HashMap<>();public int numWays(int n) {if (n <= 2) return n; // if 判断比计算状态判断开销小，因此先进行 iffinal Integer integer = statusRecord.get(n); // 计算状态判断，已经计算直接返回if (integer != null) return integer;int count = 0; // 最终结果int count1 = numWays(n - 1); // 返回中间变量int count2 = numWays(n - 1); // 返回中间变量int count = count1 + count2; // 中间变量计算结果为最终结果statusRecord.put(n, count); // 计算的结果保存至状态表return count;
}// 至此除了数据溢出问题没有处理，重复计算已优化。

自顶向下的范式套入实现：

/*** 自顶向下的范式套入实现：* * - 寻找递推关系* 自底向上递推关系为，f(n) = f(n-1) + f(n-2) 相当于从 n-1 的计算过程，先从 n 找到 1，然后在从 1 累加到 n 的过程* 我们改为从 1-n 的过程，f(i+1) = f(i) + f(i-1) ， i+1==n 时计算结束，累加的过程变量需要我们提取为中间变量参数* * - 创建新函数，将「自底向上-范式」中的最终结果计算依赖的中间变量提取为函数的参数* 将 f(i)，f(i-1) 的变量保存，初始调用我们使用 f(2) = f(1) + f(0) = 1 + 1 作为初始状态* * - 寻找基本情况，跳出时返回基本情况的结果与中间变量的计算结果（最终结果）-> if (i >= n) return a + b;* * - 根据函数参数与中间变量重新计算出新的中间变量* f(i) = f(i-1) + f(i-2) = a + b* f(i+1) = f(i) + f(i-1) = (a+b) + b* * - 修改参数 -> i + 1 递进一步* * - 递归调用并返回（该处的返回由基本情况条件触发）*/
public int numWaysTail(int n) {if (n < 2) return n;return numWaysTailHelp(n, 2, 1, 1);
}private int numWaysTailHelp(int n, int i, int a, int b) {if (i >= n) return a + b;return numWaysTailHelp(n, i + 1, a + b, a);
}// 因为是从 1-n 的计算，所以不会出现重复计算过程。

自顶向下的尾递归再优化为循环结构：（也称为动态规划 ）

public int numWaysFor(int n) {if (n < 2) return n;int i = 2; int a = 1; int b = 1; // 与尾递归 numWaysTailHelp 一致int count = a + b; // 保存次数，将尾递归的返回值提取为变量while (i <= n) { // 1-n 的过程  // 因为 f(i) = f(i-1) + f(i-2) = a + b // 下次迭代时 f(i+1) = f(i) + f(i-1) = (a+b) + bcount = a + b;b = a;a = count;i++;}return count;
}

5. 案例实战-合并两个有序的链表（多递推公式情况）

因为合并是一个条件判断的过程，因此我们在分析中要充分分析不同的条件分支。

• 基本情况：L1 或者 L2有一个为空时，不为空的节点即为头节点
• 递推公式：因为合并时涉及条件判断，所以有两种递推公式
  • L1>=L2时：merge(L1,L2)=L1+merge(L1.next,L2)，此时 L1 为头节点
  • L1<L2时：merge(L1,L2)=L2+merge(L1,L2.next)，此时 L2 为头节点

自底向上的范式验证：

public ListNode mergeTwoLists(ListNode l1, ListNode l2) {if (null == l1) return l2; // 基本情况，返回头节点if (null == l2) return l1; // 基本情况，返回头节点if (l1.val <= l2.val) { // 决定使用哪个递推公式ListNode mergeResult = mergeTwoLists(l1.next, l2); // 寻找基本情况l1.next = mergeResult;  // 使用递归函数的返回值与当前参数进行计算，该处计算为链表链接指向return l1; // 返回计算后的头节点} else {ListNode mergeResult = mergeTwoLists(l1, l2.next); // 寻找基本情况l2.next = mergeResult; // 使用递归函数的返回值与当前参数进行计算，该处计算为链表链接指向return l2; // 返回计算后的头节点}
}

当涉及到条件判断时，可能会出现多个基本情况、递推公式，我们在递归函数中逐一处理即可。
这个多公式案例理解让我们可以分析更为复杂递推关系，本质上就是范式的逐步套入、优化的过程。

6. 再谈自顶向下、自底向上

一般情况，我们说递归时指的是「自底向上」，因为「自顶向下」的过程往往需要创建新函数去完成，更甚至「自顶向下」其实就是循环结构封装为函数式编程的写法，也叫尾递归。
自底向上转换为自顶向下的过程其实就是转换为循环结构写法的过程。

递归难以理解的地方在于自底向上的过程，其实细化该难点可以分为「基本情况」->「改变参数继续递归」->「拿到递归返回值与当前参数计算」。
实际编码中我们只要按上述提到的范式进行代码编写，上述示例中的基本情况比较单一，中间变量也只涉及一个，对于复杂的跳出及中间变量的处理只要按范式步骤进行分析然后再优化一定可以写出一个递归函数。

对于递推关系的寻找过程，没有范式可寻，需要见多识广（🙉刷刷刷🙉），不断总结。

7. 递归算法推荐

• 力扣-递归标签相关算法
• 力扣-卡片-二叉树
• [力扣-卡片-递归] I(https://leetcode-cn.com/explore/featured/card/recursion-i/)

总结

简单的总结为：

• 你要写哪种类型的递归，从上算还是从下算，这决定了你如何确认递推关系
• 分析基本情况
• 寻找递推关系，在递推关系中提取中间变量
• 套入上文中的递归范式
• 按上文中的优化点进行优化
  题外话：对于自上而下的计算不是必须创建新函数去传入中间变量，因为有时我们可以使用全局变量保存、或者直接修改当前递推关系中的变量即可。
  推荐使用总结内容「自顶向下、自底向上、循环结构」三种方法完成力扣-206. 反转链表
  题解链接

转载链接：https://leetcode-cn.com/circle/article/koSrVI/