【问题描述】[简单]

【解答思路】

1. 双指针

时间复杂度：O(N+M) 空间复杂度：O(1)

class Solution {
public:bool isSubsequence(string s, string t) {int n = s.length(), m = t.length();int i = 0, j = 0;while (i < n && j < m) {if (s[i] == t[j]) {i++;}j++;}return i == n;}
};

2. 动态规划（后续挑战 ）

第 1 步：设计状态
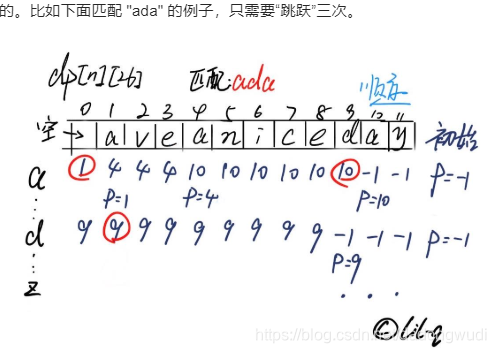
f[i][j] 表示字符串 tt 中从位置 ii 开始往后字符 jj 第一次出现的位置
第 2 步：状态转移方程

第 3 步：考虑初始化
//终止判断标志
for (int i = 0; i < 26; i++) {
f[m][i] = m;
}
第 4 步：考虑输出

时间复杂度：O(N) 空间复杂度：O(1)

class Solution {public boolean isSubsequence(String s, String t) {int n = s.length(), m = t.length();int[][] f = new int[m + 1][26];for (int i = 0; i < 26; i++) {f[m][i] = m;}for (int i = m - 1; i >= 0; i--) {for (int j = 0; j < 26; j++) {if (t.charAt(i) == j + 'a')f[i][j] = i;elsef[i][j] = f[i + 1][j];}}int add = 0;for (int i = 0; i < n; i++) {if (f[add][s.charAt(i) - 'a'] == m) {return false;}add = f[add][s.charAt(i) - 'a'] + 1;}return true;}
}

【总结】

1. 动态规划流程

第 1 步：设计状态
第 2 步：状态转移方程
第 3 步：考虑初始化
第 4 步：考虑输出
第 5 步：考虑是否可以状态压缩

2.动态规划方案避免了每次匹配都需要扫描一遍 T ，每处理一次子串只需要扫描一遍Si即可

转载链接：https://leetcode-cn.com/problems/is-subsequence/solution/pan-duan-zi-xu-lie-by-leetcode-solution/