What’s the future of the world’s coral reefs?

世界珊瑚礁的未来是什么？

In February of 2020, scientists at University of Hawaii Manoa released a study addressing this very question. The models they developed forecasted a 70–90% worldwide loss of coral by 2040. Even more alarming, they projected that “few to zero suitable coral habitats will remain” by the year 2100.

2020年2月，夏威夷大学马诺阿分校的科学家发布了一项针对这一问题的研究 。 他们开发的模型预测，到2040年，全球珊瑚损失将达到70-90％。更令人震惊的是，他们预测，到2100年，“将几乎没有零个合适的珊瑚栖息地”。

So, the future of coral doesn’t look great.

因此，珊瑚的未来看起来并不美好。

Interested in seeing these numbers firsthand, today we will develop our own forecasts of hard corals in the Caribbean. After restructuring the data, we’ll fit an extremely famous time series model: ARIMA. ARIMA has been popularized due to its simplicity and specific ability to fit time series data. Once we have a working model, we’ll develop a forecast.

有兴趣直接看到这些数字，今天我们将对加勒比地区的硬珊瑚进行预测。 重组数据后，我们将拟合一个非常著名的时间序列模型： ARIMA 。 由于ARIMA的简单性和适应时间序列数据的特定能力，它已得到普及。 建立工作模型后，我们将进行预测。

Let’s jump right in.

让我们跳进去。

为什么需要汇总？ (Why do you need to aggregate?)

We’ll start by taking a look at our raw data. In this case, we are going to be building a univariate model, so we’re only concerned with hard coral percent cover (i.e. the estimated percentage of hard coral on the sea floor).

我们将从查看原始数据开始。 在这种情况下，我们将建立一个单变量模型，因此我们只关心硬珊瑚百分比覆盖率(即海底硬珊瑚的估计百分比)。

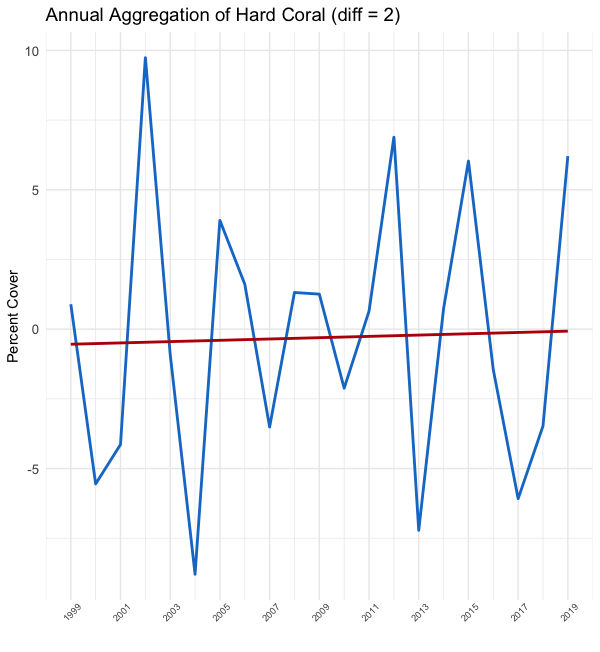
In the figure to the left, we have plotted the daily average of hard coral over time (blue). The y-axis shows the percent cover and the x-axis shows the date, ranging from 1997–2019. We also plotted a weighted linear regression line (red) to depict the overall trend.

在左图中，我们绘制了一段时间内硬珊瑚的日平均值(蓝色)。 y轴显示覆盖率百分比，x轴显示日期，范围为1997–2019。 我们还绘制了加权线性回归线(红色)以描绘总体趋势。

Ok, seems straight-forward.

好吧，似乎很简单。

But if we try to interpret these data, we see a blue mess with a negative trend line; there appears to be little systematic movement. Moreover, according to the regression line, hard coral only decreased by around 4% over the past 22 years. That’s pretty hard to believe. So, as creative and skilled data scientists, let’s try some manipulations and see if we can develop a clearer picture.

但是，如果我们尝试解释这些数据，则会看到蓝色的混乱趋势线为负； 似乎很少有系统的运动。 此外，根据回归线，硬珊瑚在过去22年中仅下降了约4％。 很难相信。 因此，作为富有创造力和技能的数据科学家，让我们尝试一些操作，看看是否可以得出更清晰的图景。

First, it’s important to know how the data are organized. Unlike most time series datasets, these data were sampled at different locations around the Caribbean with few subsequent draws at the same site. Moreover, they are not equally sampled over time. So, to account for the above points, let’s aggregate the data by time.

首先，了解数据的组织方式非常重要。 与大多数时间序列数据集不同，这些数据是在加勒比海地区的不同位置进行采样的，随后在同一地点进行的抽奖很少。 此外，随着时间的推移，它们的采样也不同。 因此，考虑到以上几点，让我们按时间汇总数据。

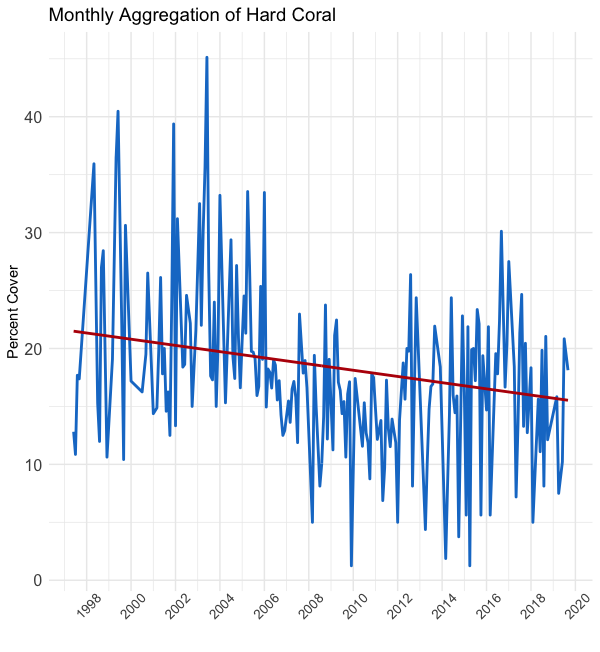
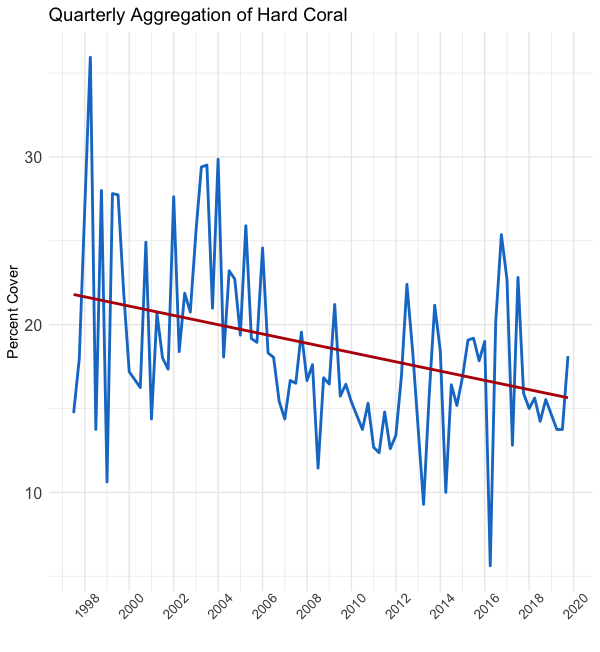
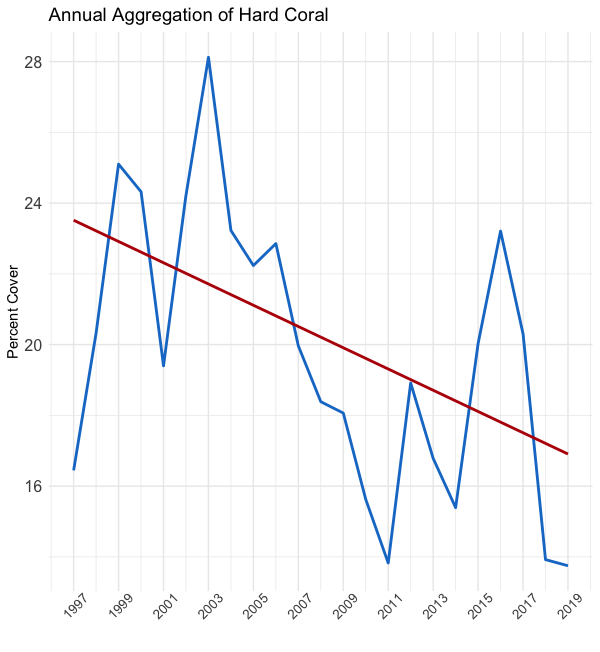
In the above figures, you can see the effect of averaging the data by monthly, quarterly, and yearly timeframes, respectively from left to right. As you “zoom out,” you reduce the variability in the data. Encompassed in this variability is both signal (good) and noise (bad). So, while the figure on the right shows the clearest trend, we’ve probably thrown out a lot of useful data.

在上图中，您可以看到分别按从左到右的每月，每季度和每年时间范围对数据进行平均的效果。 当您“缩小”时，可以减少数据的可变性。 这种可变性包括信号(好)和噪声(坏)。 因此，尽管右图显示了最明显的趋势，但我们可能已经抛弃了许多有用的数据。

To encompass the maximum and minimum amount of information, we will fit our models to both the monthly and annually aggregated data.

为了涵盖最大和最小信息量，我们将使模型适合于每月和每年汇总的数据。

Great, aggregation is done. On to our next manipulation: differencing.

很好，聚合完成了。 接下来的操作：差异化。

为什么需要与众不同？ (Why do you need to difference?)

As a practical matter, most time series models assume something called stationary. In short, strong stationary means that each data point is pulled from the same theoretical probability distribution. But, because we cannot know what this population distribution looks like, we assume weak stationarity and develop proxies for consistency in the data, namely a constant mean, variance, and covariance over time.

实际上，大多数时间序列模型都采用称为平稳的模型。 简而言之，强平稳意味着每个数据点都从相同的理论概率分布中提取。 但是，由于我们不知道总体分布是什么样子，因此我们假设平稳性较弱，并开发了数据一致性的代理，即随时间推移的均值，方差和协方差。

If you recall in the aggregation plots above, we saw a trend, indicating the mean is not constant over time. Furthermore, while the variance is harder to eyeball, there appears to be less spread in the data from 2006 to 2012. After performing a Dickey-Fuller unit root test, our observations proved correct; the monthly and annually aggregated datasets are not stationary.

如果您回想起上面的聚合图，我们看到了一个趋势，表明平均值在一段时间内不是恒定的。 此外，虽然方差更难引起注意，但2006年至2012年的数据散布似乎较少。在进行了Dickey-Fuller单位根检验后，我们的观察证明是正确的。 每月和每年汇总的数据集不是固定的。

So, to make the data useable for the ARIMA model, we will perform differencing, which simply involves subtracting each value from its prior value.

因此，为了使数据可用于ARIMA模型，我们将执行差分，这仅涉及从其先前值中减去每个值。

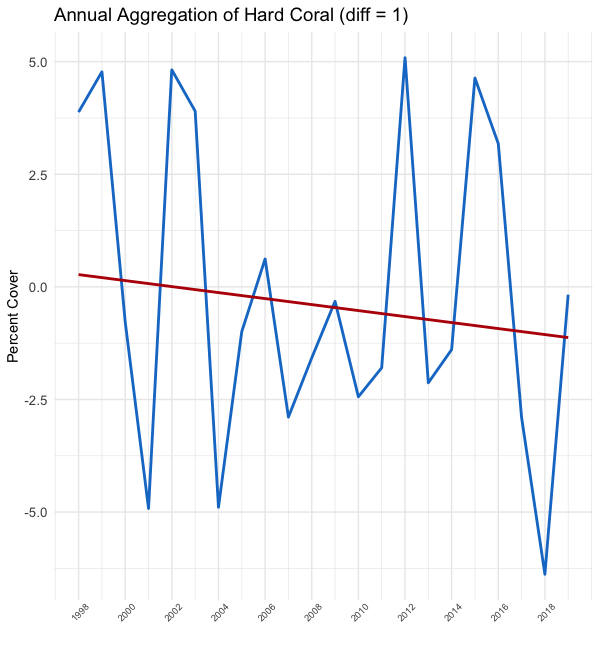
As you can see in the plots above, the y-axis values completely change from plot to plot. The leftmost plot, our un-differenced data, shows percent cover ranging from 12% to 28%. However, in the middle plot we are now working with the first difference, which shows the year over year change ranging from -6%-(+6%). The rightmost plot shows the second difference, or biannual change, with the y-axis range doubled as compared to our first-differenced plot.

如您在上面的图中所看到的，y轴值在每个图之间完全改变。 最左边的图(我们的未差异数据)显示覆盖率范围从12％到28％。 但是，在中间图中，我们正在处理第一个差异，该差异显示逐年变化范围为-6％-(+ 6％)。 最右边的图显示了第二个差异，即半年变化，y轴范围与我们的一阶差异图相比增加了一倍。

Not only does the y-axis change but the red trend line appears to flatten and the variance becomes more consistent over time. Lovely. This is what we wanted.

随着时间的推移，不仅y轴发生变化，红色趋势线也趋于平坦，并且方差变得更加一致。 可爱。 这就是我们想要的。

To double check, we again use the unit root test and find that annual data with a difference of 2 passes the stationarity test.

为了再次检查，我们再次使用单位根检验，发现相差2的年度数据通过了平稳性检验。

So, after performing similar steps for the monthly data, our datasets are now good to go. Ready to model?

因此，在对月度数据执行类似的步骤之后，现在可以使用我们的数据集了。 准备建模了吗？

调整ARIMA模型 (Tuning the ARIMA Model)

ARIMA is three-part model that combines autoregressive (AR), integration (I), and moving average (MA) components. First, the AR component looks back at prior values in our data and uses them to fit the current value. Second, the I component simply means the data are differenced, the same concept we discussed above. And third, the MA component looks back a prior errors in our fit and uses them to predict the current value.

ARIMA是三部分模型，结合了自回归(AR)，积分(I)和移动平均(MA)组件。 首先， AR组件回顾数据中的先前值，并使用它们来拟合当前值。 其次， I组件只是意味着数据有所不同，与我们上面讨论的概念相同。 第三， MA组件会根据我们的拟合情况回顾先前的错误，并使用它们来预测当前值。

It’s not necessary to understand exactly how this works, but if you’re a knowledge loving person, this YouTube playlist does a great job of explaining ARIMA models (it’s also probably the best youtube tutorial I’ve ever seen).

不必确切了解其工作原理，但是如果您是一个知识渊博的人，那么此YouTube播放列表可以很好地解释ARIMA模型(这也是我见过的最好的youtube教程)。

In its most basic form, ARIMA has three tuning parameters:

在最基本的形式中，ARIMA具有三个调整参数：

• p: how many prior values we use to fit the current value (i.e. for annual data, how many prior years of data should have an impact on the current year’s value).

  p ：我们使用多少个先前值来拟合当前值(即，对于年度数据，多少个先前年份的数据应该对当年的值产生影响)。

• d: how many times we difference.

  d ：我们相差多少次。

• q: how many prior errors we use to fit the current value.

  q ：我们使用多少个先前误差来拟合当前值。

Note that we’ve already found d, so we just need to find p and q. To do this, we will use autocorrelation plots, which are shown below in Figures 8–9.

注意，我们已经找到了d ，所以我们只需要找到p和q即可。 为此，我们将使用自相关图，如下图8–9所示。

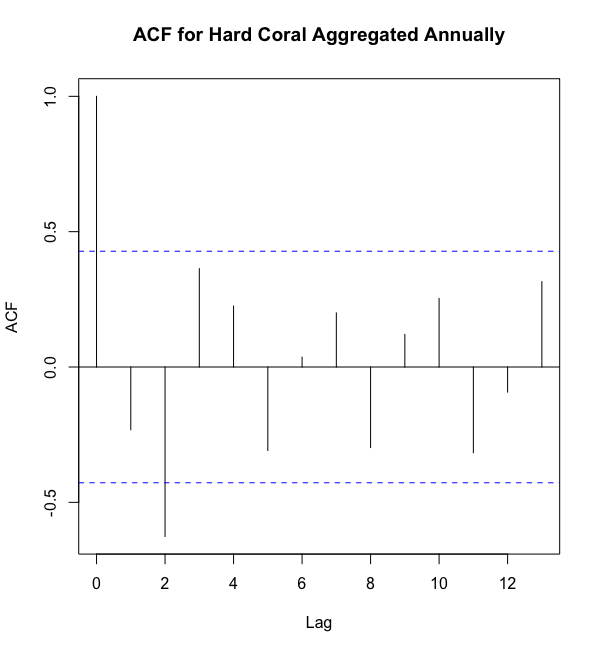
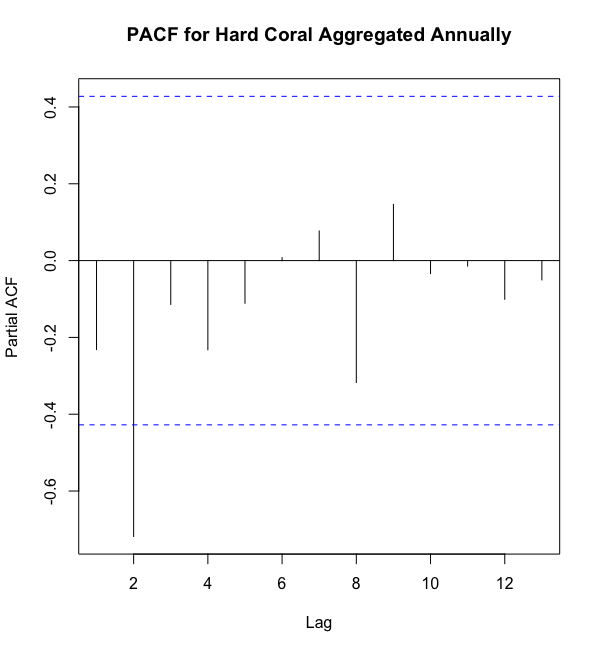
But why are there two plots? I thought there was only one variable: hard coral. That’s an outstanding point. If you’re a visual learner, check this out.

但是为什么会有两个地块？ 我以为只有一个变量：坚硬的珊瑚。 这是一个突出的观点。 如果你是一个视觉学习者，检查这出。

Either way, here’s a short explanation. The AutoCorrelation Function (ACF) plot on the left shows the correlation between hard coral now and hard coral at prior time periods, in this case years. The x-axis shows the number of years back we’re looking, and the y-axis shows the correlation between current hard coral and hard coral at the lagged time. The PartialAutoCorrelation Function (PACF) plot is very similar, however it also adjusts for the correlations of the values between the current time period and our lag by holding them constant. That’s why PACF is Partial; it doesn’t show all the correlations, whereas ACF does.

无论哪种方式，这里都有一个简短的解释。 左侧的自相关函数(ACF)图显示了现在的硬珊瑚与以前时间段(在这种情况下为几年)中的硬珊瑚之间的相关性。 x轴显示了我们正在寻找的年份，y轴显示了当前的硬珊瑚与滞后时间的硬珊瑚之间的相关性。 PartialAutoCorrelation Function(PACF)图非常相似，但是它也通过将它们保持不变来调整当前时间段与我们的滞后值之间的相关性。 这就是为什么PACF是Partial； 它没有显示所有相关性，而ACF却显示了所有相关性。

In practice, we use the ACF plot to determine how many prior years are important for the AutoRegressive (AR) component. We then use the PACF to determine the Moving Average (MA) portion of the model. These values are called orders.

在实践中，我们使用ACF图来确定多少年对于自动回归(AR)组件很重要。 然后，我们使用PACF来确定模型的移动平均(MA)部分。 这些值称为订单。

As you can see, the ACF plot has significant lags at 0 and 2, as indicated by a correlation greater than our significance threshold (blue dotted line). Note that a lag of 0 is simply the same time period, so a correlation of 1.0 makes sense. Applying the same process to the PACF plot, we can see a significant lag at 2. This leaves us with a p=2 and q=2. So, our annual ARIMA(p, d, q) would take the form ARIMA(2,2,2).

如您所见，ACF图在0和2处有明显的滞后，其相关性大于我们的显着性阈值(蓝色虚线)。 请注意，滞后0只是同一时间段，因此1.0的相关性是有意义的。 将相同的过程应用于PACF图，我们可以看到在2处有明显的滞后。这使我们剩下p = 2和q = 2 。 因此，我们的年度ARIMA( p ， d，q )将采用ARIMA(2,2,2)的形式。

Wow, that was a lot of setup, but now we’re well-equipped for fitting the data.

哇，这是很多设置，但是现在我们有足够的设备来拟合数据。

培训ARIMA (Training ARIMA)

Here we will be looking at 3 different models, namely:

在这里，我们将研究3种不同的模型，即：

1. ARIMA(2,2,2) with annual aggregation (developed above).
   具有年度汇总的ARIMA(2,2,2)(如上开发)。
2. ARMIA(3,1,1) with monthly aggregation.
   ARMIA(3,1,1)，每月汇总。
3. ARIMA(6,1,1) with monthly aggregation.
   每月汇总的ARIMA(6,1,1)。

To evaluate each models’ performance, we will use the squared correlation between the model’s fitted values and the true values; the r-squared closest to 1.0 is the winner.

为了评估每个模型的性能，我们将使用模型的拟合值和真实值之间的平方相关性。 最接近1.0的R平方是获胜者。

每月汇总 (Monthly Aggregation)

Our ARIMA(3,1,1) model doesn’t perform great, exhibiting an r-squared valued of 0.156. We then run our ARIMA(6,1,1) model and get a very similar r-squared of 0.170. Unfortunately, it doesn’t look like we’re doing a great job of fitting.

我们的ARIMA(3,1,1)模型执行不佳，其r平方值为0.156。 然后，我们运行ARIMA(6,1,1)模型，得到非常相似的r平方0.170。 不幸的是，看起来我们并没有做得很好。

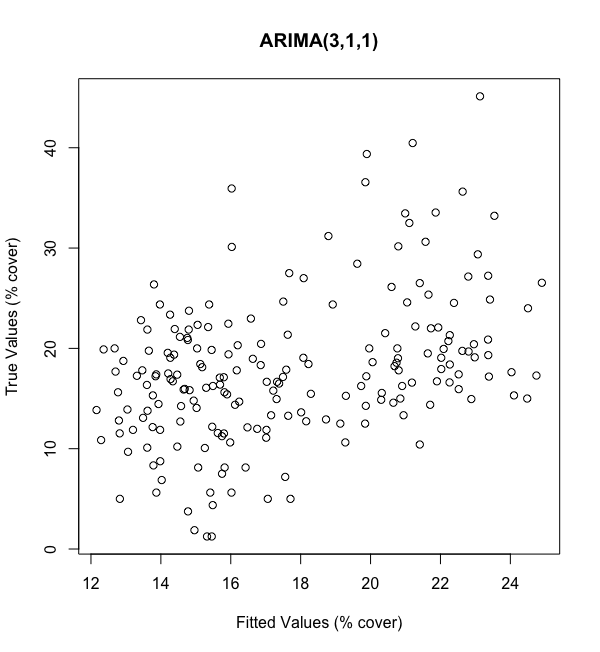
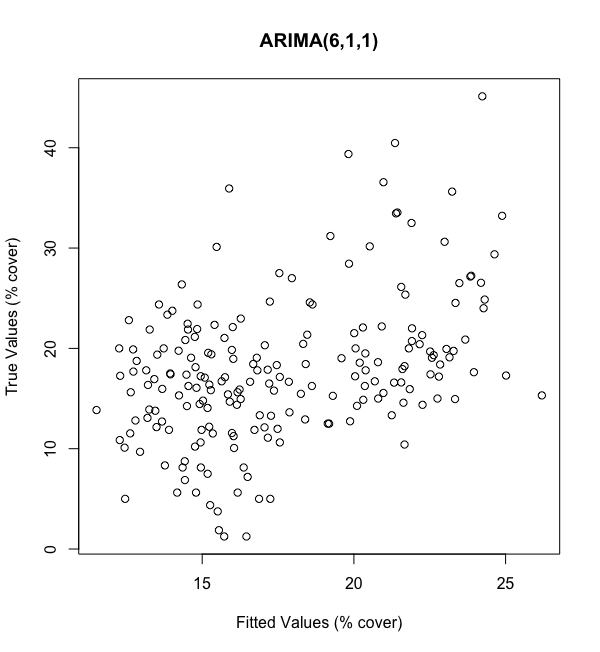
As show above in Figures 10–11, our poor fit is reflected by the lack of systematic trend between our fitted values (x-axis) and true values (y-axis). It also seems like our range of fitted values is far smaller than our true range; we’re off by about 15 percentage points in the high and low ends. So, not only is the fit bad, the scaling of the fit is bad as well.

如图10-11所示，拟合值(x轴)和真实值(y轴)之间缺乏系统的趋势反映了我们的拟合度较差。 看起来我们的拟合值范围远远小于我们的真实范围； 我们在高端和低端市场上下降了约15个百分点。 因此，不仅拟合度很差，而且拟合度也很差。

年度汇总 (Annual Aggregation)

Luckily, annual aggregation comes in to save the day with an r-squared of 0.689, indicating a very good fit (given the data).

幸运的是，年度汇总可以节省时间，且r平方为0.689，表明该数据非常合适(根据数据)。

As shown in the plot to the left, we have the true values in blue as compared to the fitted values in yellow. The fit looks pretty good, although it seems like the model is capturing the trend a little too late. Moreover, we don’t see the extreme scaling difference observed in the monthly models; instead, the fitted values are more extreme than the true data, as shown in 2003 and 2014. That being said, this appears to be a reasonable fit.

如左图所示，蓝色的真实值与黄色的拟合值相比。 拟合看起来不错，尽管看起来该模型捕捉趋势有点太晚了。 此外，我们没有看到在每月模型中观察到极端的比例差异； 相反，拟合值比真实数据更极端，如2003年和2014年所示。也就是说，这似乎是一个合理的拟合。

So, why did annual aggregation perform so much better? Well, it appears that our annual aggregation was able to smooth out the noise, allowing the model to accurately decipher trends. That being said, you can’t help but wonder what information was also thrown out by averaging.

那么，为什么年度汇总表现要好得多？ 好吧，看来我们的年度汇总能够消除噪声，从而使模型可以准确地解释趋势。 话虽这么说，您不禁要问平均也会抛出哪些信息。

In hopes of improving fits for both the monthly and annual models, the following variations were tested:

为了改善月度和年度模型的拟合度，对以下变化进行了测试：

• Adding a seasonal component with orders (3,0,1) and (6,0,1). Note this was only done for monthly data, but worsened the fit in both cases.
  添加订单为(3,0,1)和(6,0,1)的季节性成分。 请注意，此操作仅针对月度数据进行，但两种情况下的拟合均变差。

• Fitting with a predictor dummy variable: [1, 2, …, n-1, n]. This helped the fit significantly.

  拟合预测变量：[1,2，…， n-1 ， n ]。 这极大地帮助了拟合。

• Testing different p, d, q values (+/- 1), which worsened the fit.

  测试不同的p ， d ， q值(+/- 1)，这会使拟合度变差。

Ok, fairly confident we have maximized our training fit, let’s move on to forecasting.

好吧，非常有信心我们已经最大限度地提高了训练水平，让我们继续进行预测。

ARIMA预测 (Forecasting With ARIMA)

Here we are going to predict the next 5 years of hard coral coverage using our annual ARIMA(2,2,2) model with the above dummy predictor.

在这里，我们将使用具有上述虚拟预测器的年度ARIMA(2,2,2)模型预测未来5年的硬珊瑚覆盖率。

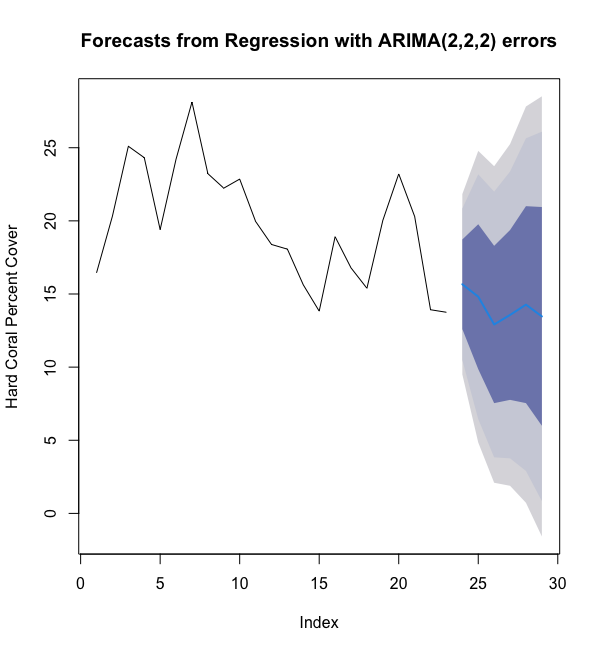
As indicated by the light blue trend line (in the dark shaded region), the forecasted percent cover is negative but not precipitous; the predicted value for 2025 is 13.46% cover. Moreover, the error bands are so large it’s impossible to make precise conclusions.

如浅蓝色趋势线所示(在深色阴影区域中)，预测的覆盖率百分比为负，但并不险峻； 到2025年的预测价值是13.44％的覆盖率。 而且，误差带太大，不可能得出准确的结论。

That being said, the error bands do provide interpretive power. The dark blue, dark grey, and light grey bands correspond to a 67%, 90%, and 95% confidence interval respectively. This means, for instance, that we are 67% confident that 5 years from now our percent cover will be between 5.99 and 20.95.

话虽如此，误差带确实提供了解释力。 深蓝色，深灰色和浅灰色带分别对应67％，90％和95％的置信区间。 例如，这意味着我们有67％的信心，从现在开始的5年后，我们的覆盖率范围将在5.99到20.95之间。

To further interpret these confidence intervals, according to our model’s 95% confidence interval, we are 97.5% certain that we will not lose all hard coral in the Caribbean over the next 4 years. However, note that on the 5th year, this statement does not hold. Now looking at the upper side of our 95% confidence interval, we are 97.5% certain that in the next 5 years we will not surpass 29% cover, roughly corresponding to our our 22-year high observed in 2003.

为了进一步解释这些置信区间，根据我们模型的95％置信区间，我们有97.5％的把握将在未来4年内不会失去加勒比海所有坚硬的珊瑚。 但是，请注意，在第5年，此声明不成立。 现在来看我们95％的置信区间的上限，我们97.5％的人相信在未来5年中，我们的覆盖率将不会超过29％，大致相当于我们在2003年所创的22年高点。

Well that was interesting, but a bit underwhelming. To produce a more precise forecast, we’ll have to try other techniques (hint: there will be a part 2).

嗯，这很有趣，但是有点让人印象深刻。 为了产生更精确的预测，我们将不得不尝试其他技术(提示：第2部分)。

结论 (Conclusion)

Three major takeaways from today’s analysis:

当今分析的三个主要收获：

1. The Reef Check measures of hard coral do not provide much autoregressive signal until they are aggregated annually. That being said, we are exploring other aggregation methods, for instance our prior post.

   硬珊瑚的“珊瑚礁检查”措施在每年进行汇总之前不会提供很多自回归信号。 话虽如此，我们正在探索其他汇总方法，例如我们先前的post 。

2. Using univariate ARIMA, we can get a training r-squared of around 0.7 which is pretty good for such noisy data — just think about all the factors that can impact hard coral.
   使用单变量ARIMA，我们可以获得约0.7的训练R平方，对于这样的嘈杂数据来说，这是非常好的-只需考虑可能影响硬珊瑚的所有因素即可。
3. However, our forecasts have extremely wide prediction intervals, meaning there’s a lot of uncertainty.
   但是，我们的预测具有非常宽的预测间隔，这意味着存在很多不确定性。

In following posts, we will add predictor variables to our time series model. We will also try other models to see if they produce better results. If you have ideas on where to go, leave a comment or reach out here.

在接下来的文章中，我们将预测变量添加到时间序列模型中。 我们还将尝试其他模型，看看它们是否产生更好的结果。 如果您有去哪里的想法，请在此处发表评论或联系。

资料来源 (Sources)

• Cryer, J. D., & Chan, K. (2011). Time series analysis with applications in R. New York: Springer.

  Cryer，JD，＆Chan，K.(2011年)。 时间序列分析及其在R中的应用 。 纽约：施普林格。

• Hyndman, R. J., & Athanasopoulos, G. (2018). Forecasting: Principles and practice. Melbourne: OTexts.

  Hyndman，RJ和Athanasopoulos，G.(2018年)。 预测：原理和实践 。 墨尔本：OTexts。

• Warming, acidic oceans may nearly eliminate coral reef habitats by 2100. (n.d.). Retrieved September 02, 2020, from https://news.agu.org/press-release/warming-acidic-oceans-may-nearly-eliminate-coral-reef-habitats-by-2100/

  到2100年，变暖的酸性海洋几乎可以消除珊瑚礁的栖息地。 于2020年9月2日从https://news.agu.org/press-release/warming-acidic-oceans-may-nearly-eliminate-coral-reef-habitats-by-2100/中检索

The data were collected by Reef Check, a coral conservation non-profit that trains volunteer divers to collect marine data. With 1576 unique entries for the Caribbean ranging from 1997–05–24 to 2019–08–24, there were plenty of data points to conduct a TS analysis. However, the sampling variation differs greatly across location and time period. To combat this, we performed aggregation over time, however the difference in location still posed analysis problems. We largely ignored these, but analysis determining whether sampling location has a significant impact is required to derive conclusions.

数据是由珊瑚礁非营利组织Reef Check收集的，该组织培训志愿潜水员收集海洋数据。 从1997–05–24到2019–08–24，在加勒比地区共有1576个唯一条目，其中有大量数据点可以进行TS分析。 但是，采样变化在位置和时间段之间差异很大。 为了解决这个问题，我们随时间进行了汇总，但是位置的差异仍然带来了分析问题。 我们在很大程度上忽略了这些，但是需要分析确定采样位置是否具有重大影响才能得出结论。

Here is the code.

这是代码 。

Note: these are my findings. If you would like to contact me, leave a message here. All criticisms are welcome.

注意：这些是我的发现。 如果您想与我联系，请在此处留言。 欢迎所有批评。