PCB钻孔时,当钻刀>6.3mm时,超出钻孔范围,钻孔工序是没有这么大的钻刀,当这种情况,工程CAM会都采用G84命令用小孔扩孔的方式制作, 在这里介绍一种如果不用G84命令,用程序实现将大孔生成小孔钻孔达到扩孔的目的。
一.我们先了解一下G84命令扩孔
孔尺寸大小

孔密度

连一篇文章有关于孔数计算方式: https://www.cnblogs.com/pcbren/p/9379178.html
二.求解思路
1.通过孔密度,求出孔与孔中心距离
2.求出单次增量方位角
3.以大孔中心为,长度为(大孔半径-小孔半径), 任选择一个方位角作为起始方位角,并增加一个起始孔,并围绕这个起始方位角不断递增方位角,直到360度递增完成后即结束。
三.C#简易代码实现:
1.扩孔钻孔代码


string drilllayer = "drl";gLayer layer = g.getFEATURES($"{drilllayer}", g.STEP, g.JOB, "mm", true);List<gPP> pList = new List<gPP>();double HoleSize = 3175; //扩孔所用钻刀大小foreach (var pad in layer.Plist){if (pad.width > 6300) //钻孔>6300需扩孔 {gA arc = calc2.p_2A(new gP(pad.p, pad.width - HoleSize));arc.width = HoleSize;var HoleCenterDi = calc2.p_Convex(arc.width * 0.0005)*3;pList.AddRange(calc2.a_2Plist(arc, HoleCenterDi, 2, true));}}addCOM.pad(pList);
2.计算函数


/// <summary>/// 通过孔半径与凸高位求 孔中心距/// </summary>/// <param name="Rradius">孔半径</param>/// <param name="tol_">凸位高度值</param>/// <returns></returns>public double p_Convex(double Rradius, double tol_ = 0.0127){return Math.Sqrt(Math.Pow(Rradius, 2) - Math.Pow(Rradius - tol_, 2)) * 2;}/// <summary>/// 求方位角/// </summary>/// <param name="ps"></param>/// <param name="pe"></param>/// <returns></returns>public double p_ang(gPoint ps, gPoint pe){double a_ang = Math.Atan((pe.y - ps.y) / (pe.x - ps.x)) / Math.PI * 180;//象限角 转方位角 计算所属象限 并求得方位角if (pe.x >= ps.x && pe.y >= ps.y) //↗ 第一象限 {return a_ang;}else if (!(pe.x >= ps.x) && pe.y >= ps.y) // ↖ 第二象限 {return a_ang + 180;}else if (!(pe.x >= ps.x) && !(pe.y >= ps.y)) //↙ 第三象限 {return a_ang + 180;}else if (pe.x >= ps.x && !(pe.y >= ps.y)) // ↘ 第四象限 {return a_ang + 360;}else{return a_ang;}}//求方位角/// <summary>/// 求增量坐标/// </summary>/// <param name="ps">起点</param>/// <param name="val">增量值</param>/// <param name="ang_direction">角度</param>/// <returns></returns>public gPP p_val_ang(gPP ps, double val, double ang_direction){gPP pe = ps;pe.p.x = ps.p.x + val * Math.Cos(ang_direction * Math.PI / 180);pe.p.y = ps.p.y + val * Math.Sin(ang_direction * Math.PI / 180);return pe;}/// <summary>/// 弧Arc 转点P组集/// </summary>/// <param name="a"></param>/// <param name="val_">此数值表示:分段数值</param>/// <param name="type_">代表值数值类型 【0】弧长 【1】角度 【2】弦长 </param>/// <param name="is_avg">是否平均分布 </param>/// <returns></returns>public List<gPP> a_2Plist(gA a, double val_ = 0.1d, int type_ = 0, bool is_avg = false){List<gPP> list_point = new List<gPP>();gPP tempP;tempP.p = a.ps;tempP.symbols = a.symbols;tempP.width = a.width;list_point.Add(tempP);double avg_count;double angle_val = 0;double rad_ = p2p_di(a.pc, a.pe);double sum_alge = a_Angle(a);if (type_ == 1) // 【1】角度 {angle_val = val_;avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - 1; // 总角度/单角度 }else if (type_ == 2) //【2】弦长 {angle_val = Math.Asin(val_ / (rad_ * 2)) * 360 / pi;avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - 1; // 总角度/单角度 }else // 【0】弧长 {angle_val = val_ * 180 / (pi * rad_);avg_count = (int)(Math.Ceiling(sum_alge / angle_val)) - 1; // 总角度/单角度//avg_count = (int)(Math.Ceiling(a_Lenght(a) / val_)) - 1; // 或 总弧长/单弧长 }if (is_avg)angle_val = sum_alge / avg_count;if (avg_count > 1){gPP centerP = tempP;centerP.p = a.pc;double angle_s = p_ang(a.pc, a.ps);if (a.ccw) { angle_val = 0 - angle_val; }for (int i = 1; i < avg_count; i++){tempP = p_val_ang(centerP, rad_, angle_s - angle_val * i);list_point.Add(tempP);}}if (!(zero(a.ps.x - a.pe.x) && zero(a.ps.y - a.pe.y))){tempP.p = a.pe;list_point.Add(tempP);}return list_point;}/// <summary>/// 返回两点之间欧氏距离/// </summary>/// <param name="p1"></param>/// <param name="p2"></param>/// <returns></returns>public double p2p_di(gPoint p1, gPoint p2){return Math.Sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));}/// <summary>/// 求弧Arc圆心角 //后续改进 用叉积 与3P求角度求解 验证哪个效率高/// </summary>/// <param name="a"></param>/// <returns></returns>public double a_Angle(gA a){double angle_s, angle_e, angle_sum;if (a.ccw){angle_s = p_ang(a.pc, a.pe);angle_e = p_ang(a.pc, a.ps);}else{angle_s = p_ang(a.pc, a.ps);angle_e = p_ang(a.pc, a.pe);}if (angle_s == 360) { angle_s = 0; }if (angle_e >= angle_s)angle_sum = 360 - Math.Abs(angle_s - angle_e);elseangle_sum = Math.Abs(angle_s - angle_e);return angle_sum;}/// <summary>/// 检查值决对值 小于 (eps = 0.001) 浮点误差处理/// </summary>/// <param name="x"></param>/// <returns></returns>public bool zero(double x){return (((x) > 0 ? (x) : (-x)) < eps);}
3.Point,PAD,Arc数据结构


/// <summary>/// 精简 PAD 数据类型/// </summary>public struct gPP{public gPP(double x_val, double y_val, double width_){this.p = new gPoint(x_val, y_val);this.symbols = "r";this.width = width_;}public gPP(gPoint p_, double width_){this.p = p_;this.symbols = "r";this.width = width_;}public gPP(gPoint p_, string symbols_, double width_){this.p = p_;this.symbols = symbols_;this.width = width_;}public gPoint p;public string symbols;public double width;public static gPP operator +(gPP p1, gPP p2){p1.p += p2.p;return p1;}public static gPP operator +(gPP p1, gPoint p2){p1.p += p2;return p1;}public static gPP operator -(gPP p1, gPP p2){p1.p -= p2.p;return p1;}public static gPP operator -(gPP p1, gPoint p2){p1.p -= p2;return p1;}}/// <summary>/// 点 数据类型 (XY)/// </summary>public struct gPoint{public gPoint(gPoint p_){this.x = p_.x;this.y = p_.y;}public gPoint(double x_val, double y_val){this.x = x_val;this.y = y_val;}public double x;public double y;public static gPoint operator +(gPoint p1, gPoint p2){p1.x += p2.x;p1.y += p2.y;return p1;}public static gPoint operator -(gPoint p1, gPoint p2){p1.x -= p2.x;p1.y -= p2.y;return p1;}}/// <summary>/// ARC 数据类型/// </summary>public struct gA{public gA(double ps_x, double ps_y, double pc_x, double pc_y, double pe_x, double pe_y, double width_, bool ccw_){this.ps = new gPoint(ps_x, ps_y);this.pc = new gPoint(pc_x, pc_y);this.pe = new gPoint(pe_x, pe_y);this.negative = false;this.ccw = ccw_;this.symbols = "r";this.attribut = string.Empty;this.width = width_;}public gA(gPoint ps_, gPoint pc_, gPoint pe_, double width_, bool ccw_ = false){this.ps = ps_;this.pc = pc_;this.pe = pe_;this.negative = false;this.ccw = ccw_;this.symbols = "r";this.attribut = string.Empty;this.width = width_;}public gPoint ps;public gPoint pe;public gPoint pc;public bool negative;//polarity-- positive negativepublic bool ccw; //direction-- cw ccwpublic string symbols;public string attribut;public double width;public static gA operator +(gA arc1, gPoint move_p){arc1.ps += move_p;arc1.pe += move_p;arc1.pc += move_p;return arc1;}public static gA operator +(gA arc1, gP move_p){arc1.ps += move_p.p;arc1.pe += move_p.p;arc1.pc += move_p.p;return arc1;}public static gA operator -(gA arc1, gPoint move_p){arc1.ps -= move_p;arc1.pe -= move_p;arc1.pc -= move_p;return arc1;}public static gA operator -(gA arc1, gP move_p){arc1.ps -= move_p.p;arc1.pe -= move_p.p;arc1.pc -= move_p.p;return arc1;}}
四.实现效果
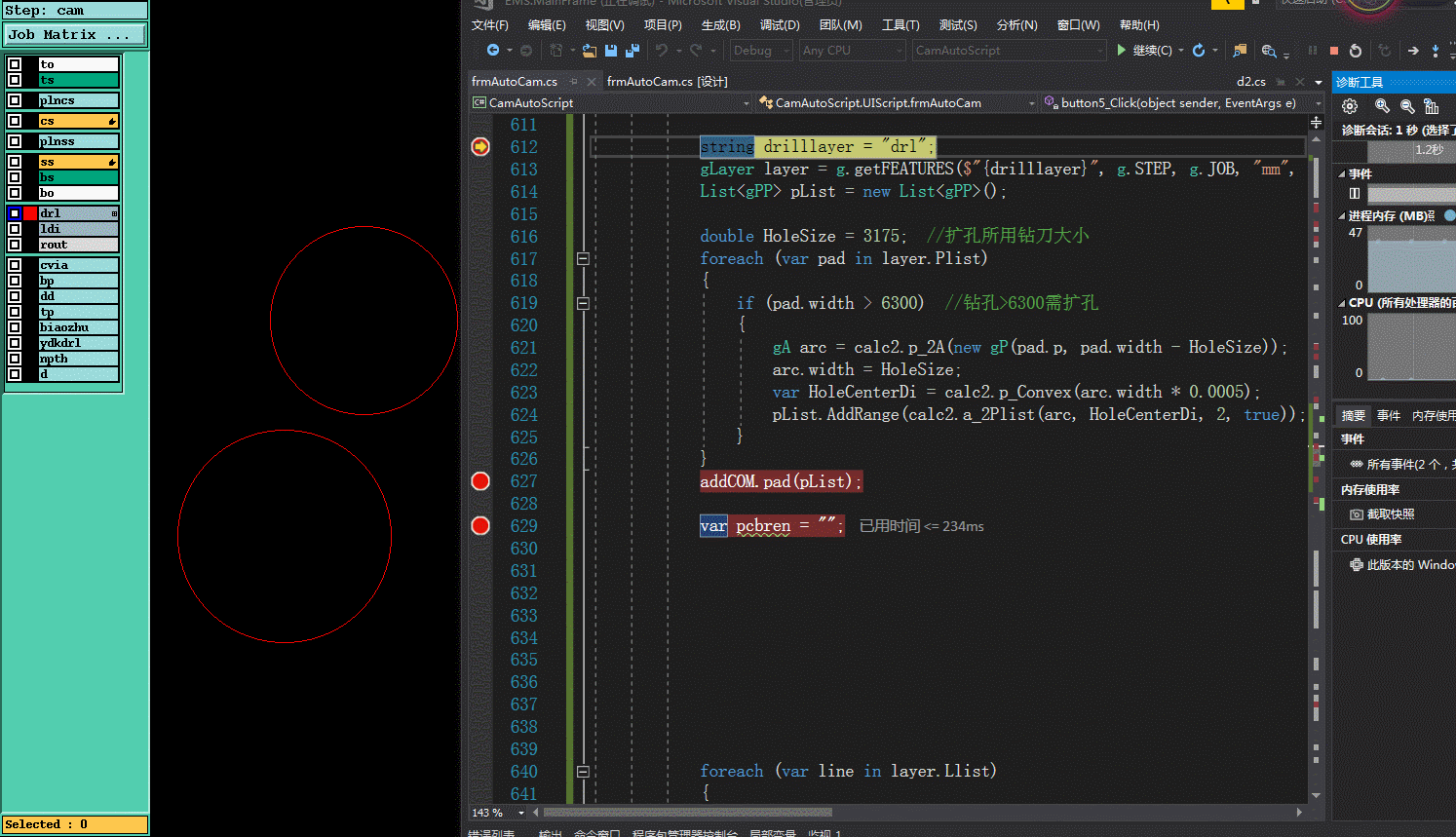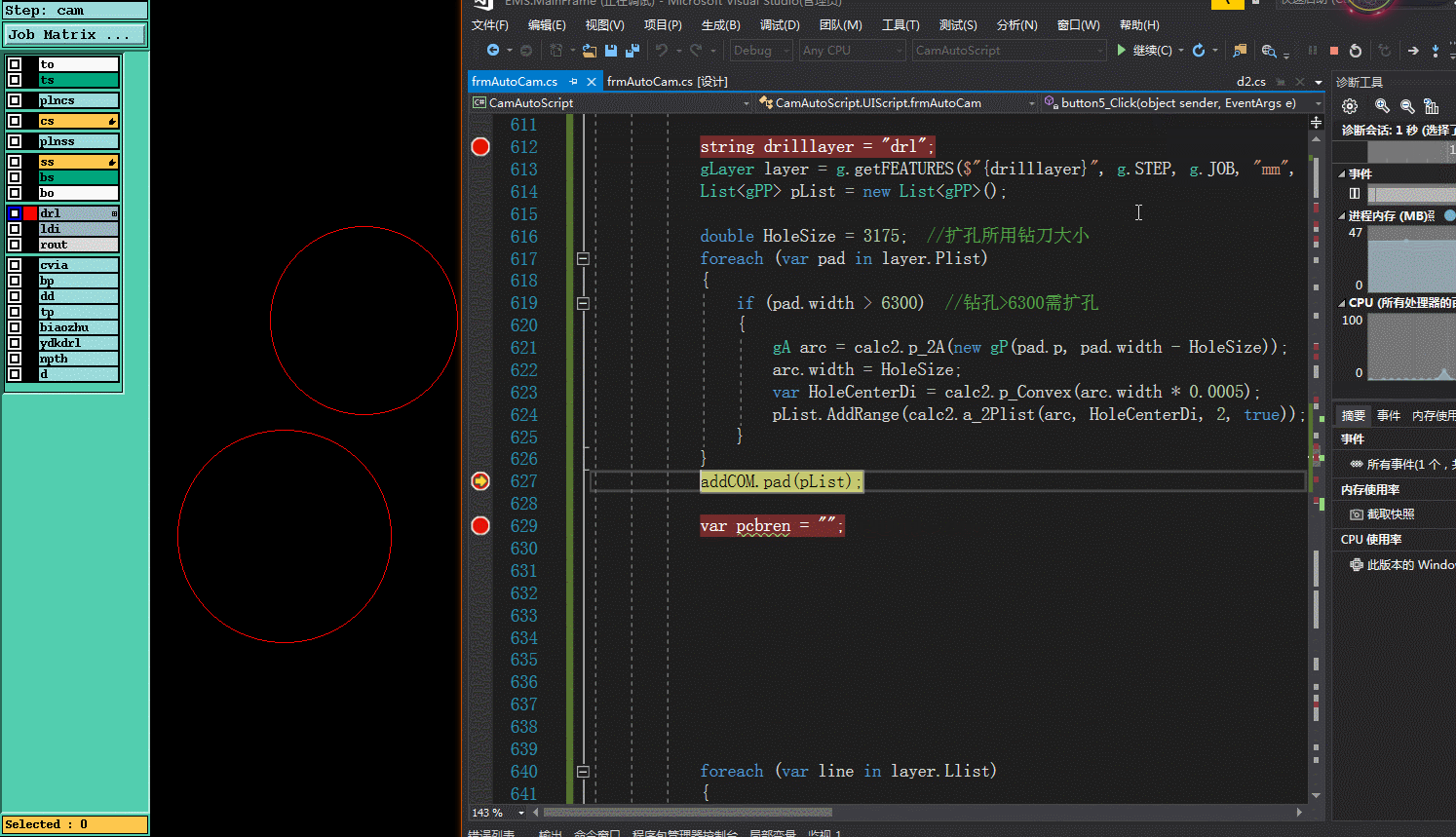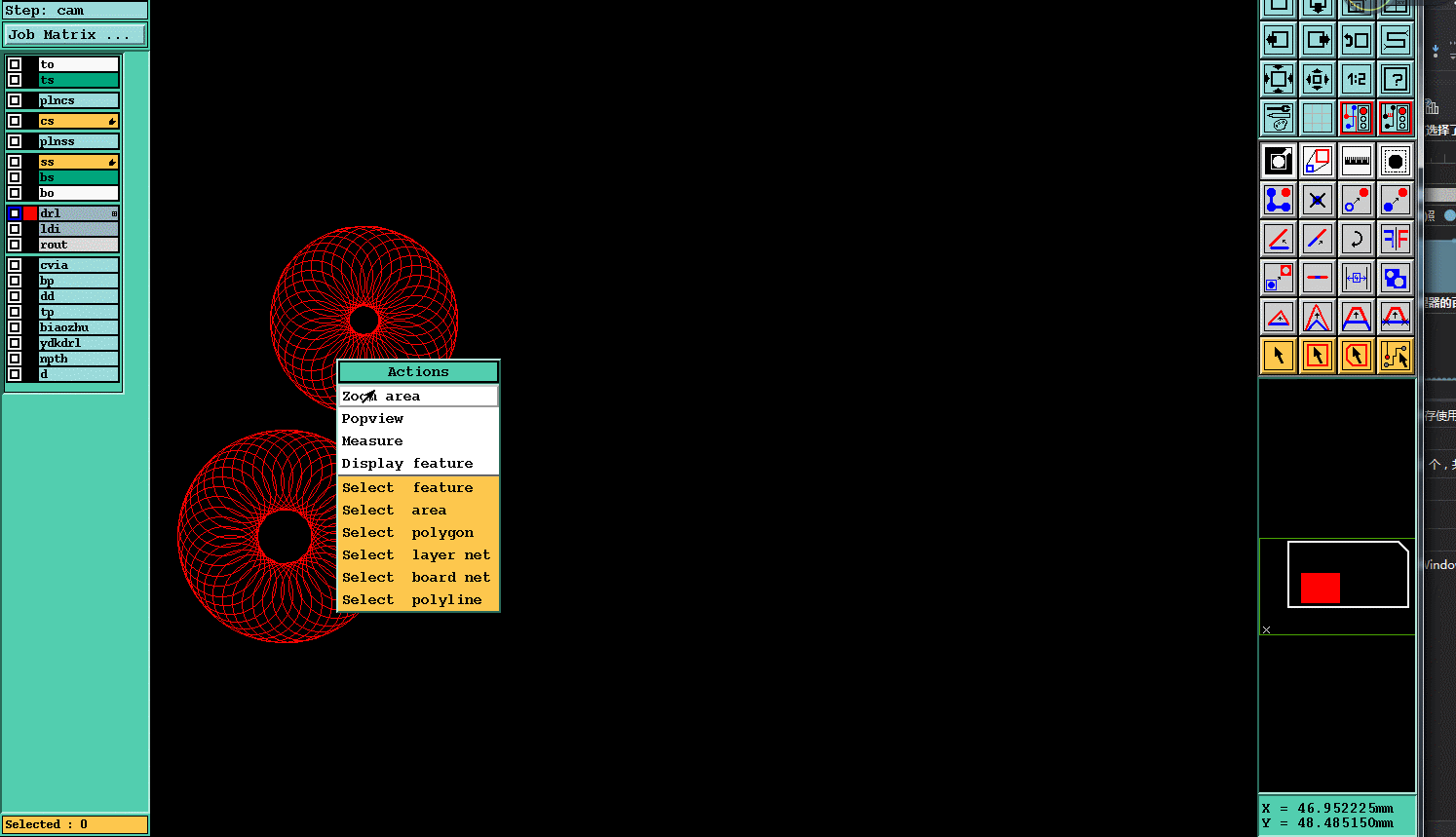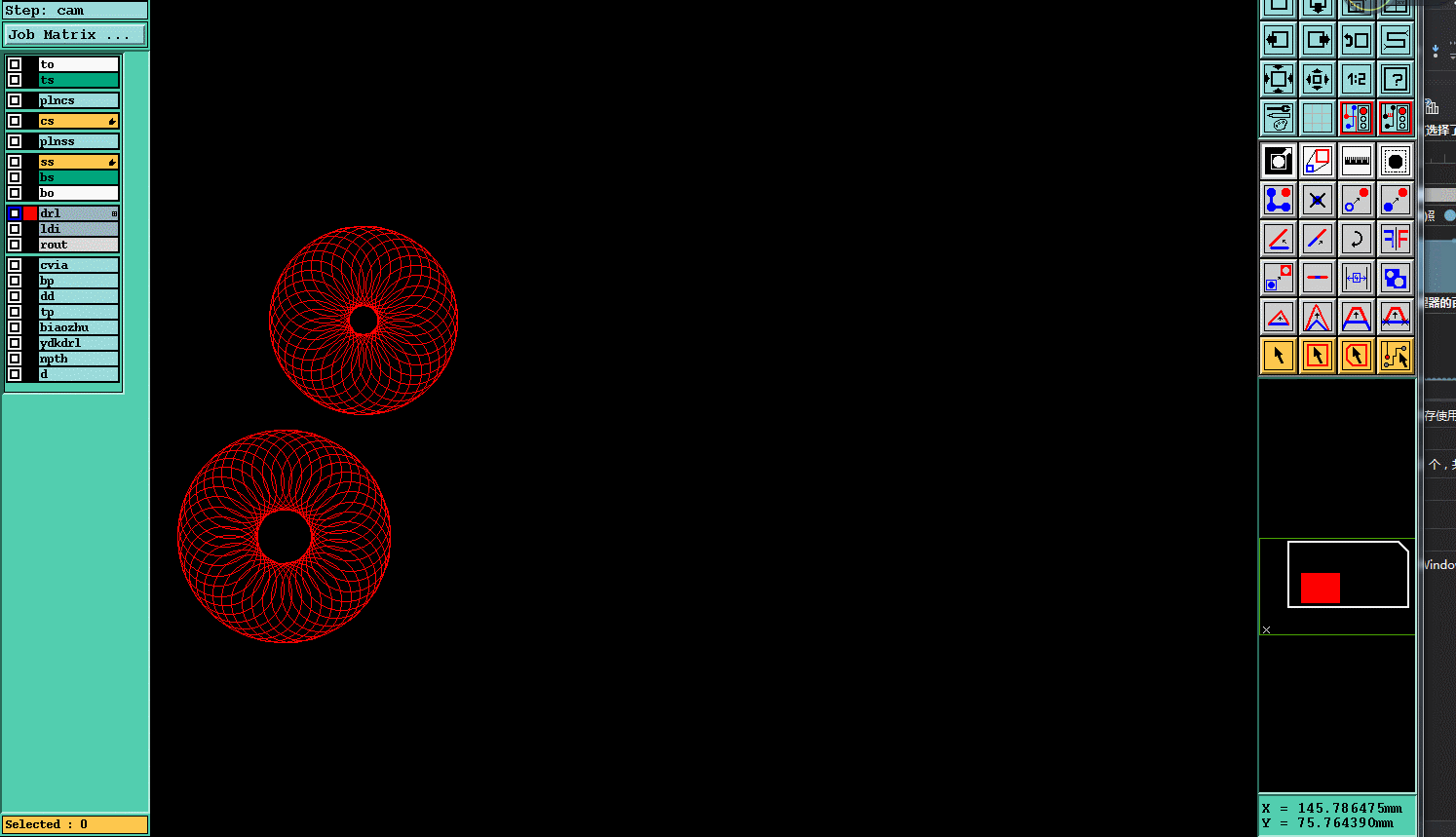

)




)











)
