python版PCA（主成分分析）

　　在用统计分析方法研究这个多变量的课题时，变量个数太多就会增加课题的复杂性。人们自然希望变量个数
较少而得到的信息较多。在很多情形，变量之间是有一定的相关关系的，当两个变量之间有一定相关关系时，可
以解释为这两个变量反映此课题的信息有一定的重叠。主成分分析是对于原先提出的所有变量，建立尽可能少的
新变量，使得这些新变量是两两不相关的，而且这些新变量在反映课题的信息方面尽可能保持原有的信息。

原理

　　设法将原来变量重新组合成一组新的互相无关的几个综合变量，同时根据实际需要从中可以取出几个较少的
综合变量尽可能多地反映原来变量的信息的统计方法叫做主成分分析或称主分量分析，也是数学上处理降维的一

种方法。

步骤

主成分分析主要步骤如下：　　

指标数据标准化；　　
指标之间的相关性判定；　
计算特征值与特征向量
计算主成分贡献率及累计贡献率
计算主成分载荷

代码

[python] view plaincopy 
 #-*- coding:utf-8 -*-  
 from pylab import *  
 from numpy import *  
   
 def pca(data,nRedDim=0,normalise=1):  
     # 数据标准化  
     m = mean(data,axis=0)  
     data -= m  
     # 协方差矩阵  
     C = cov(transpose(data))  
     # 计算特征值特征向量，按降序排序  
     evals,evecs = linalg.eig(C)  
     indices = argsort(evals)  
     indices = indices[::-1]  
     evecs = evecs[:,indices]  
     evals = evals[indices]  
     if nRedDim>0:  
         evecs = evecs[:,:nRedDim]  
   
     if normalise:  
         for i in range(shape(evecs)[1]):  
             evecs[:,i] / linalg.norm(evecs[:,i]) * sqrt(evals[i])  
     # 产生新的数据矩阵  
     x = dot(transpose(evecs),transpose(data))  
     # 重新计算原数据  
     y=transpose(dot(evecs,x))+m  
     return x,y,evals,evecs  
   
 x = random.normal(5,.5,1000)  
 y = random.normal(3,1,1000)  
   
 a = x*cos(pi/4) + y*sin(pi/4)  
 b = -x*sin(pi/4) + y*cos(pi/4)  
   
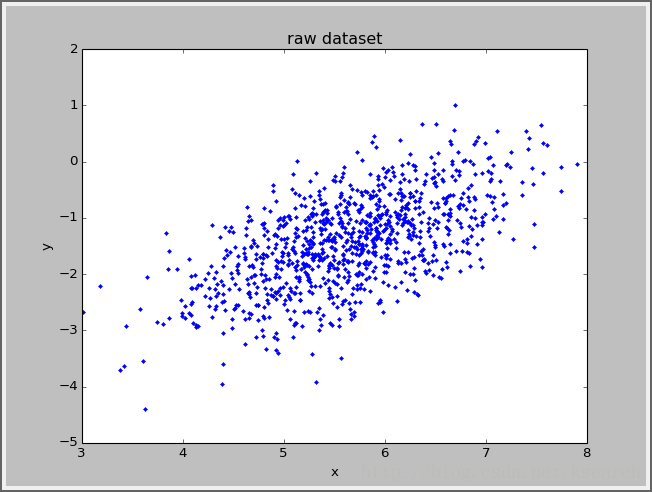
 plot(a,b,'.')  
   
 xlabel('x')  
 ylabel('y')  
   
 title('raw dataset')  
   
 data = zeros((1000,2))  
 data[:,0] = a  
 data[:,1] = b  
 x,y,evals,evecs = pca(data,1)  
 print y  
 figure()  
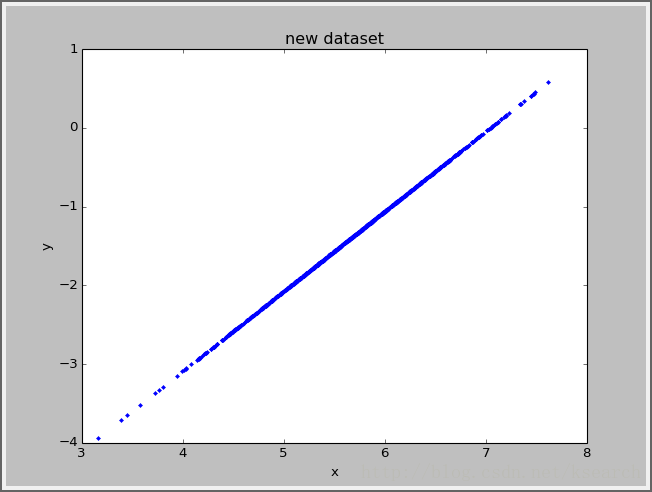
 plot(y[:,0],y[:,1],'.')  
 xlabel('x')  
 ylabel('y')  
 title('new dataset')  
 show()  