蓝桥杯方格填数(全排列+图形补齐)

方格填数

如下的10个格子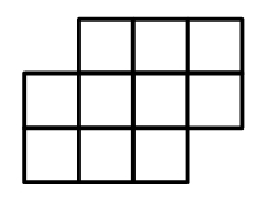

填入0~9的数字，同一数字不能重复填。要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）

一共有多少种可能的填数方案？

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

解题思路：由题可知，题中的序列是固定的，只有0-9这10个元素，所以可以枚举其全部全排列，对每个排列根据条件进行筛选。

先看一个错误答案：520　　　

(图一)

一开始想当然的把0-9存入了一维数组中，如图一，然后发现下标i的上下两个相邻位置的坐标为i-4,i+4, 左右为i-1,i+1,

左上右下为i-5,i+5，右上左下为i-3,i+3。于是有了下面的错误代码。

错误代码：（此错误代码运行结果为520）

 1 #include <iostream>
 2 #include <vector>
 3 #include <algorithm>
 4 
 5 using namespace std;
 6 
 7 vector<int>v;
 8 int a[8] = { -1,1,-3,3,-4,4,-5,5 };　　　　　//一维数组相邻点的下标
 9 
10 bool judge()
11 {
12     for (int i = 0; i <= 9; ++i)
13     {
14         for (int j = 0; j < 8; ++j)
15         {
16             int k = i + a[j];
17             if (k >= 0 && k <= 9)
18             {
19                 if (abs(v[k] - v[i]) == 1)  //相邻元素之差的绝对值为1
20                     return false;
21             }
22         }
23     }
24     return true;
25 }
26 
27 int main()
28 {
29     int cnt = 0;
30     for (int i = 0; i <= 9; ++i)
31         v.push_back(i);
32 
33     do
34     {
35         if (judge() == true)
36             cnt++;
37 
38     } while (next_permutation(v.begin(), v.end()));
39 
40     cout << cnt << endl;
41 
42     return 0;
43 }

错因：忽略了边界上的坐标，比如7，一直认为左上就是i-5，但是7-5=2，但是7并没有左上方的点。

改进：由于边界上的坐标比较难处理，所以为了消除边界的影响，将地图补全为如下规则图形，如图二，这样就消除了图二中红色区域边界上的影响：

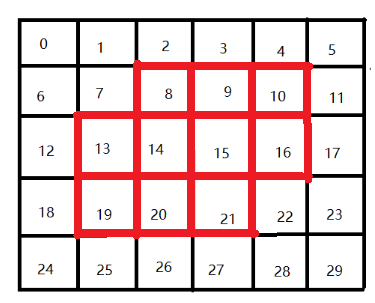（图二）

用大小为30的一维数组v保存。

用一维数组vec保存0-9，对vec进行枚举全排列，然后将vec[0...9]分别赋值给图二中的红色区域，再将非红色的区域赋值为-10，

对于图二中的红色区域，发现下标i的上下两个相邻位置的坐标为i-6,i+6, 左右为i-1,i+1,左上右下为i-7,i+7，右上左下为i-5,i+5。

此时再用根据下标获取其相邻元素的值，判断填入的数字是否相邻即可。

改进后的正确代码：

 1 #include <iostream>  
 2 #include <vector>  
 3 #include <algorithm>  
 4 
 5 using namespace std;
 6 
 7 vector<int> v;    //补全的图形
 8 vector<int> vec;  //未补全的图形
 9 int a[8] = { -1,1,-5,5,-6,6,-7,7 };    //一维数组相邻点的下标
10 
11 bool judge(vector<int> v)
12 {
13     for (int i = 8; i <= 21; ++i)
14     {
15         for (int j = 0; j < 8; ++j)    //对其所有相邻位置进行枚举
16         {
17             int k = i + a[j];
18             if (abs(v[k] - v[i]) == 1)  //相邻元素之差的绝对值为1
19                 return false;
20             
21         }
22     }
23     return true;
24 }
25 
26 int main()
27 {
28     int cnt = 0;    //方案数
29     for (int i = 0; i <= 9; ++i)
30         vec.push_back(i);    //一开始必须升序，是为了保证next_permutation能枚举所有情况的排列
31 
32     for (int i = 0; i <= 29; ++i)
33         v.push_back(-10);
34 
35     do
36     {
37         v[8] = vec[0]; v[9] = vec[1]; v[10] = vec[2]; v[13] = vec[3]; v[14] = vec[4];
38         v[15] = vec[5]; v[16] = vec[6]; v[19] = vec[7]; v[20] = vec[8]; v[21] = vec[9];
39 
40         if (judge(v) == true)
41             cnt++;
42 
43     } while (next_permutation(vec.begin(), vec.end()));
44     
45     cout << cnt << endl;
46 
47     return 0;
48 }