Matlab中有关boxplot(X)命令的解释：

boxplot(X) produces a box and whisker plot for each column of the matrix X. The box has lines at the lower quartile, median, and upper quartile values. Whiskers extend from each end of the box to the adjacent values in the data—by default, the most extreme values within 1.5 times the interquartile range from the ends of the box. Outliers are data with values beyond the ends of the whiskers. Outliers are displayed with a red + sign.

格式

boxplot(X) %产生矩阵X的每一列的盒图和“须”图，“须”是从盒的尾部延伸出来，并表示盒外数据长度的线，如果“须”的外面没有数据，则在“须”的底部有一个点。
boxplot(X,notch) %当notch=1时，产生一凹盒图，notch=0时产生一矩箱图。
boxplot(X,notch,‘sym’) %sym表示图形符号，默认值为“+”。
boxplot(X,notch,‘sym’,vert) %当vert=0时，生成水平盒图，vert=1时，生成竖直盒图（默认值vert=1）。
boxplot(X,notch,‘sym’,vert,whis) %whis定义“须”图的长度，默认值为1.5，若whis=0则boxplot函数通过绘制sym符号图来显示盒外的所有数据值。

Examples 1

The following commands create a box plot of car mileage grouped by country.

load carsmall

boxplot(MPG,Origin)

Examples 2

The following example produces notched box plots for two groups of sample data.

x1 = normrnd(5,1,100,1);

x2 = normrnd(6,1,100,1);

boxplot([x1,x2],‘notch’,‘on’)

Examples 3

x1 = normrnd(5,1,100,1);
x2 = normrnd(6,1,100,1);
boxplot([x1,x2])

The difference between the medians of the two groups is approximately 1.Since the notches in the boxplot do not overlap, you can conclude, with 95% confidence, that the true medians do differ.

Examples 4

The following figure shows the boxplot for same data with the length of the whiskers specified as 1.0 times the interquartile range. Points beyond the whiskers are displayed using +.

x1 = normrnd(5,1,100,1); x2 = normrnd(6,1,100,1); boxplot([x1,x2],‘notch’,‘on’,‘whisker’,1)

箱形图

最近有很多用户说到了年终需要回顾这一年的工作，根据这一年的数据看看有没有异常的情况，那么哪种图能够清晰直观地展现出这一信息呢？

答案只有一个，那就是…

箱形图

箱形图（英文：Box plot），又称为盒须图、盒式图、盒状图或箱线图，是一种用作显示一组数据分散情况资料的统计图。因型状如箱子而得名。在各种领域也经常被使用，常见于品质管理，快速识别异常值。

箱形图最大的优点就是不受异常值的影响，能够准确稳定地描绘出数据的离散分布情况，同时也利于数据的清洗。

想要搞懂箱形图，那么一定要了解…

五大因“数”

我们一组序列数为例：12，15，17，19，20，23，25，28，30，33，34，35，36，37讲解这五大因“数”

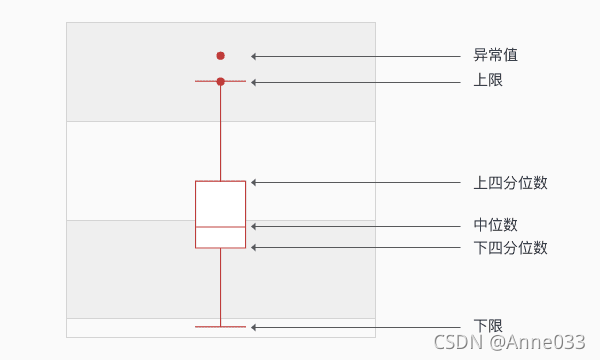
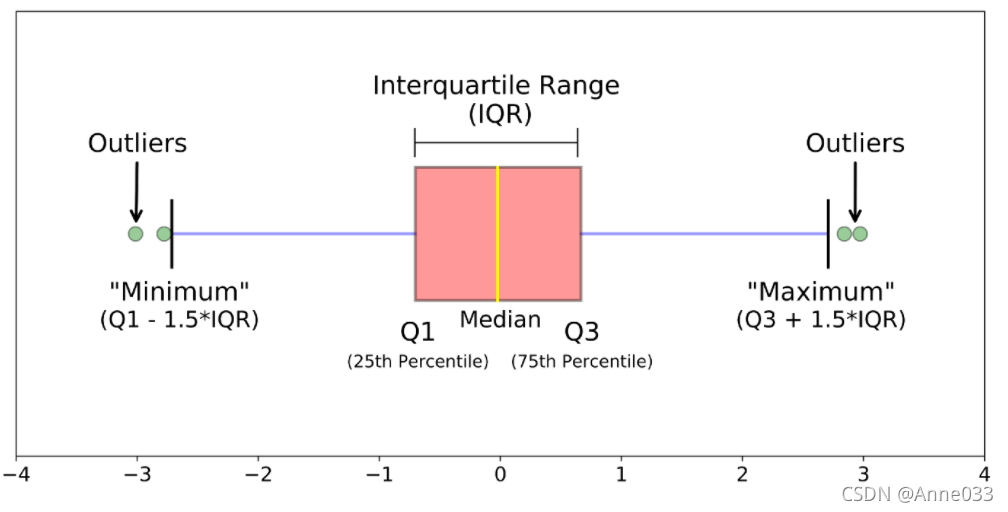
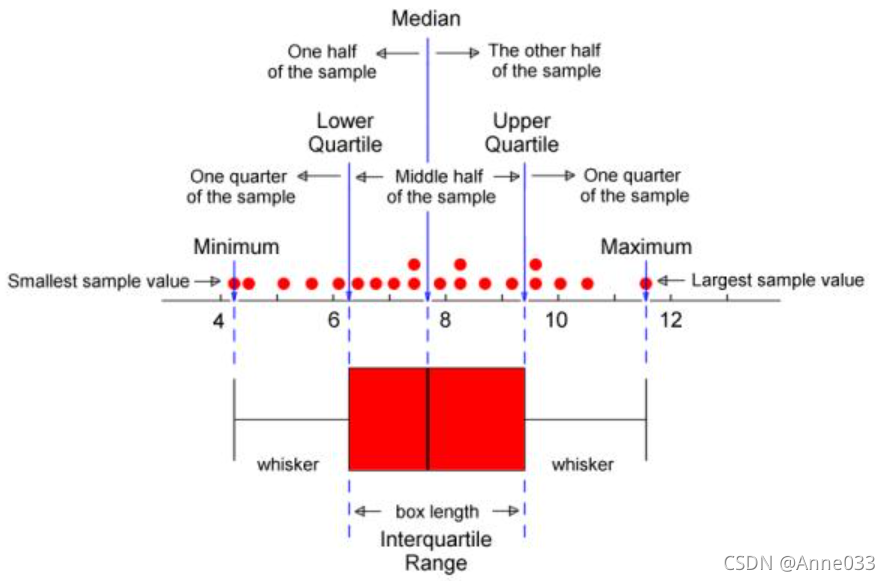
1、下四分位数Q1

（1）确定四分位数的位置。Qi所在位置=i（n+1）/4，其中i=1，2，3。n表示序列中包含的项数。

（2）根据位置，计算相应的四分位数。

例中：

Q1所在的位置=（14+1）/4=3.75，

Q1=0.25×第三项+0.75×第四项=0.25×17+0.75×19=18.5；

2、中位数（第二个四分位数）Q2

中位数，即一组数由小到大排列处于中间位置的数。若序列数为偶数个，该组的中位数为中间两个数的平均数。

例中：

Q2所在的位置=2（14+1）/4=7.5，

Q2=0.5×第七项+0.5×第八项=0.5×25+0.5×28=26.5

3、上四分位数Q3

计算方法同下四分位数。

例中：

Q3所在的位置=3（14+1）/4=11.25，

Q3=0.75×第十一项+0.25×第十二项=0.75×34+0.25×35=34.25。

4、上限

上限是非异常范围内的最大值。

首先要知道什么是四分位距如何计算的？

四分位距IQR=Q3-Q1，那么上限=Q3+1.5IQR

5、下限

下限是非异常范围内的最小值。

下限=Q1-1.5IQR

实例

讲了这么多的“数学知识”，那么箱形图到底如何通过BDP应用到实际的工作呢？我们还是用一个实例来帮助大家理解。

现在有“2017年各季度各地区分公司销售业绩”工作表，我们想要找出各季度哪些分公司业绩属于不正常范围内。

数据示例如下图：

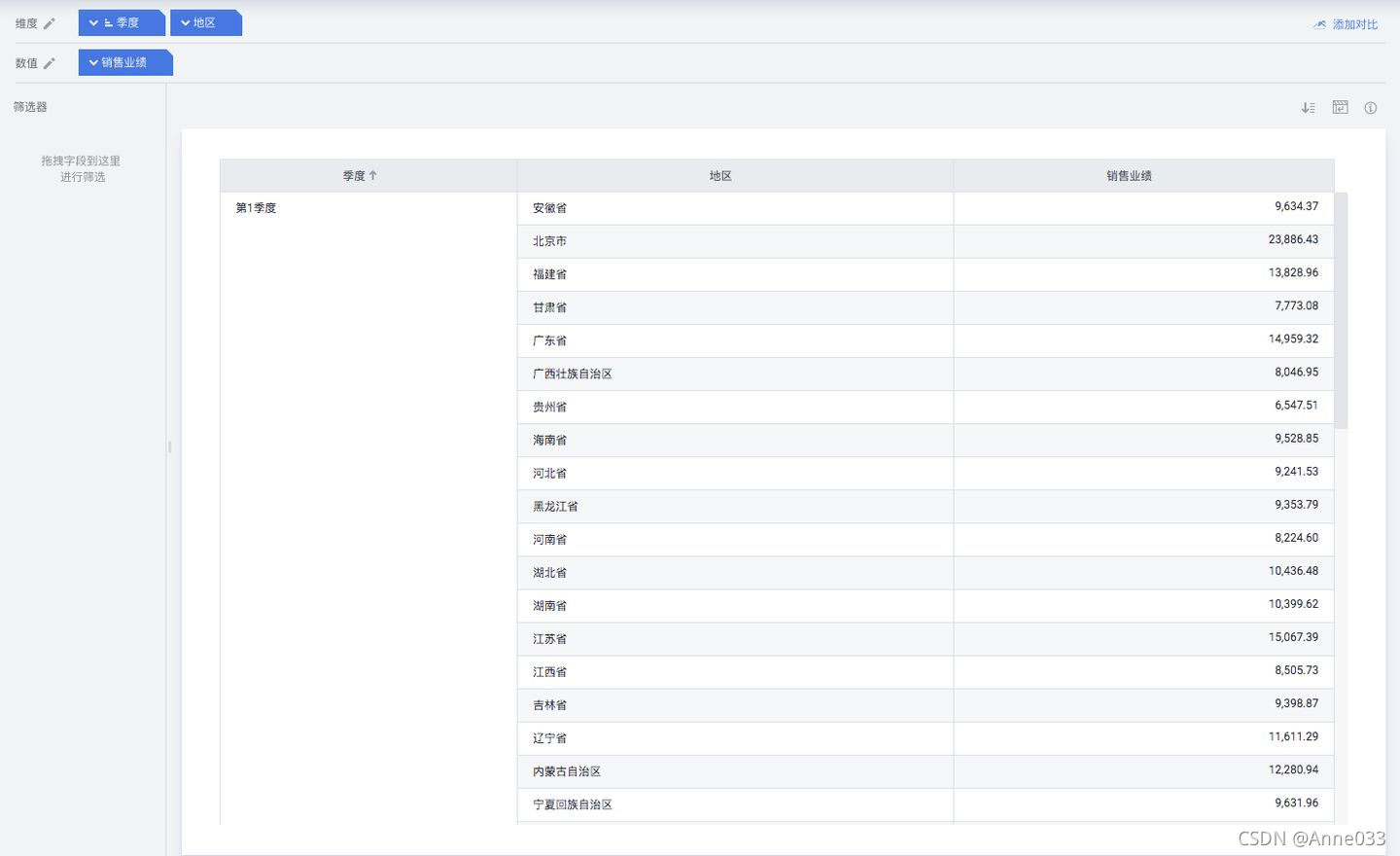
BDP箱形图结果：

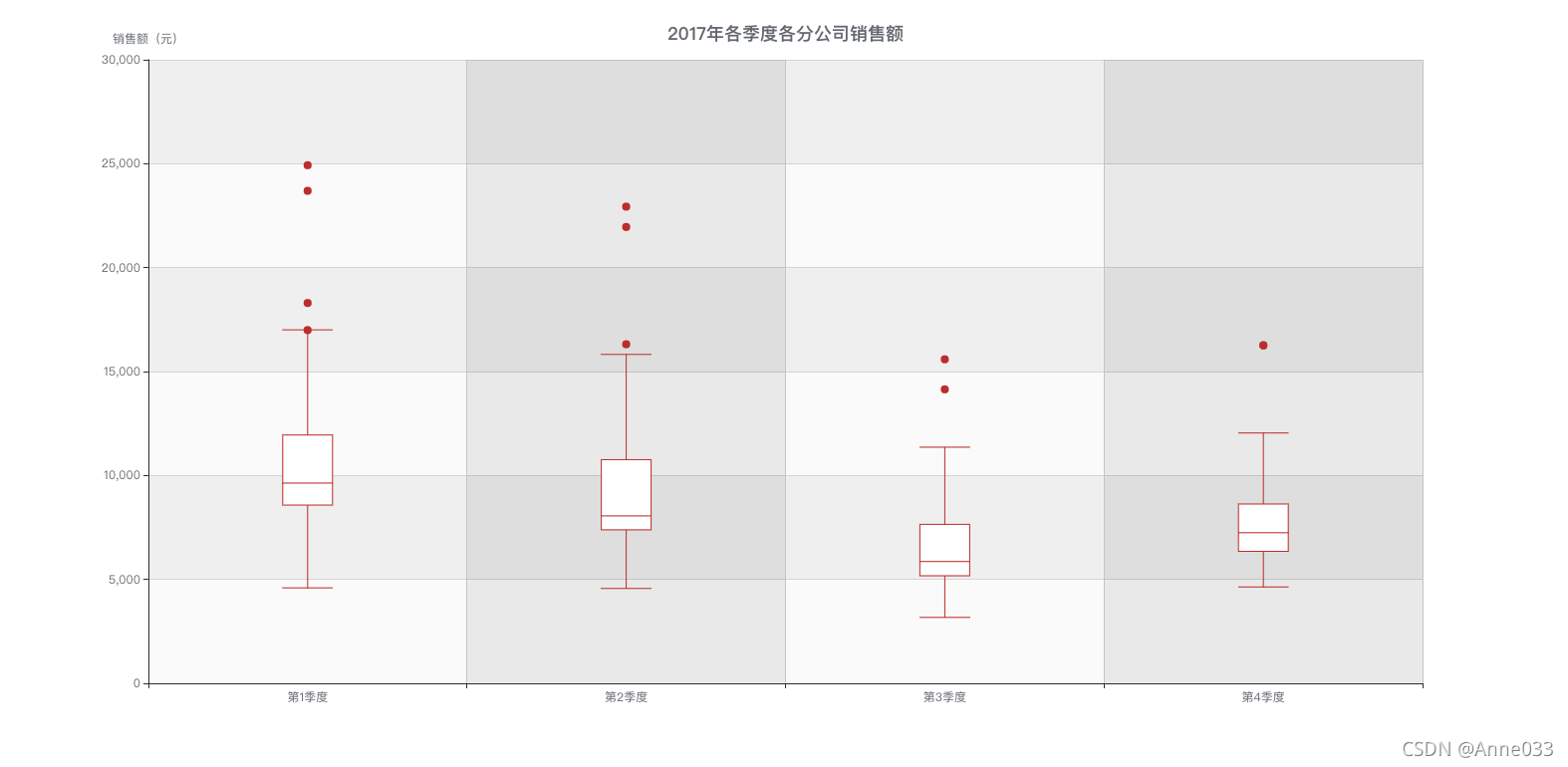
从上图可以清晰的找出异常点，例如第二季度北京分公司的销售额为22147元，该值比上限10759元还要大，所以定义为异常值。

具体操作在这里就不讲解了，可以参考“各位久等了，全新的炫酷图表终于上线啦！”

箱形图的价值

1.直观明了地识别数据批中的异常值

上文讲了很久的识别异常值，其实箱线图判断异常值的标准以四分位数和四分位距为基础，四分位数具有一定的耐抗性，多达25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值不会影响箱形图的数据形状，箱线图识别异常值的结果比较客观。由此可见，箱线图在识别异常值方面有一定的优越性。

2.利用箱线图判断数据批的偏态和尾重

对于标准正态分布的样本，只有极少值为异常值。异常值越多说明尾部越重，自由度越小（即自由变动的量的个数）；

而偏态表示偏离程度，异常值集中在较小值一侧，则分布呈左偏态；异常值集中在较大值一侧，则分布呈右偏态。

3.利用箱线图比较几批数据的形状

同一数轴上，几批数据的箱线图并行排列，几批数据的中位数、尾长、异常值、分布区间等形状信息便昭然若揭。如上图，可直观得看出第三季度各分公司的销售额大体都在下降。

局限性

但箱形图也有他的局限性，比如：不能精确地衡量数据分布的偏态和尾重程度；对于批量比较大的数据，反映的信息更加模糊以及用中位数代表总体评价水平有一定的局限性。

https://zhuanlan.zhihu.com/p/33473642