目录
一 问题背景
二 具体步骤
2.1 picgo的安装
1. 下载picgo
2. 安装
3. 效果
2.2 Node.js的安装
(1)下载链接
(2)安装步骤
2.3 Gitee设置
2.3.1在gitee上面创建一个仓库
2.4 整体配置
2.4.1 picgo软件配置
2.4.2 图床设置
2.4.3 Typora配置
三 失败问题总结
四 最终效果
参考链接
一 问题背景
实现Typora书写笔记上传至CSDN时,图片可以采用MarkDown笔记方式,直接复制粘贴。避免出现“外链图片转存失败,源站可能有防盗链机制”的问题。该博客记录踩过的坑与安装过程
二 具体步骤
2.1 picgo的安装
1. 下载picgo
- 官网下载地址:Release 2.3.0 · Molunerfinn/PicGo · GitHub
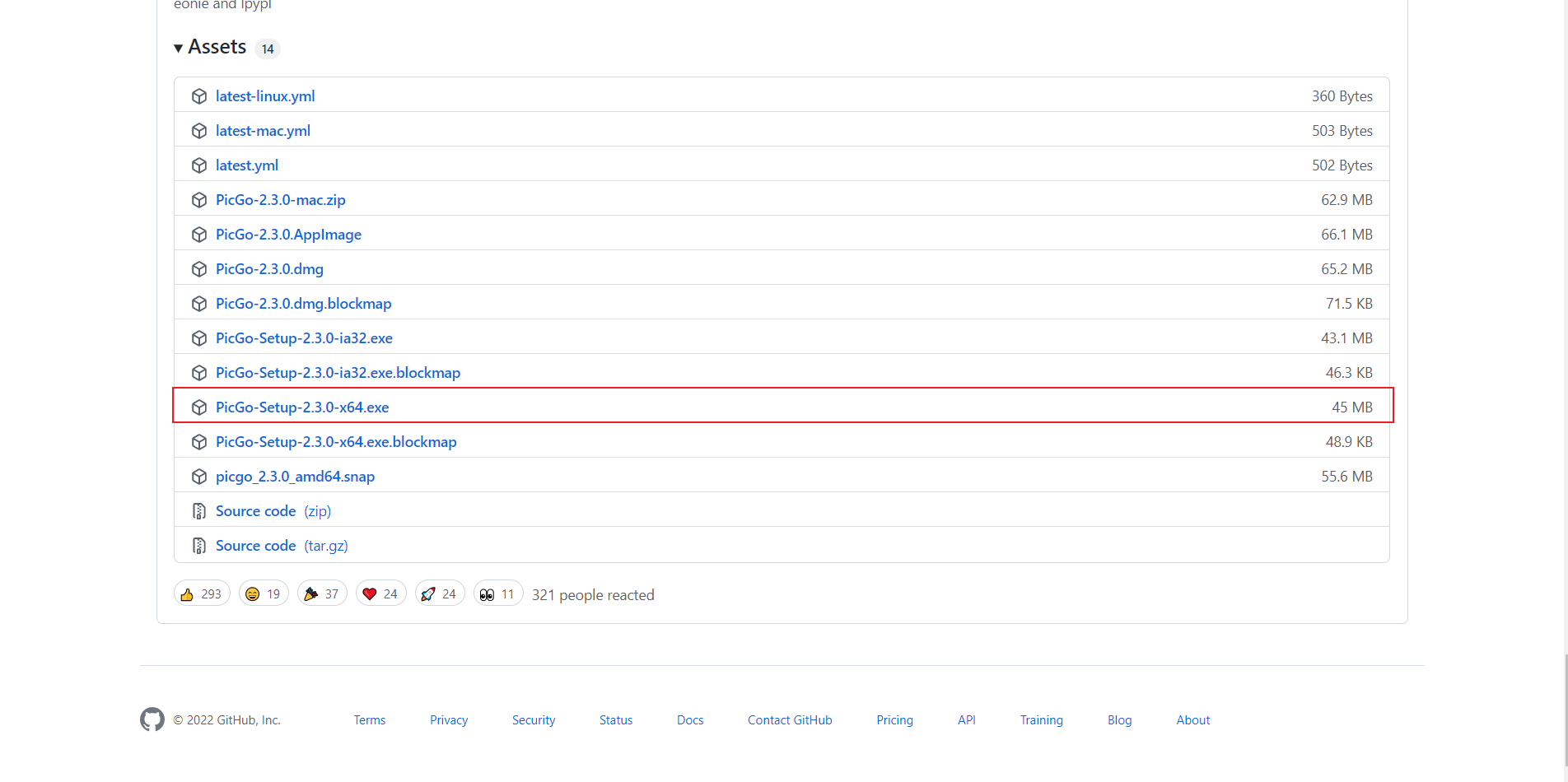
由于Github下载较慢,此处提供云盘链接
链接:https://pan.baidu.com/s/1lB1fLPU8DSOe2AQ9EeLQ2Q
提取码:x2bv
2. 安装
直接打开 .exe 文件,一步步安装即可。
3. 效果
电脑右下角-》点击后的图标即是改软件

点击界面如下
2.2 Node.js的安装
(1)下载链接
官网链接:Node.js
下载长期使用版
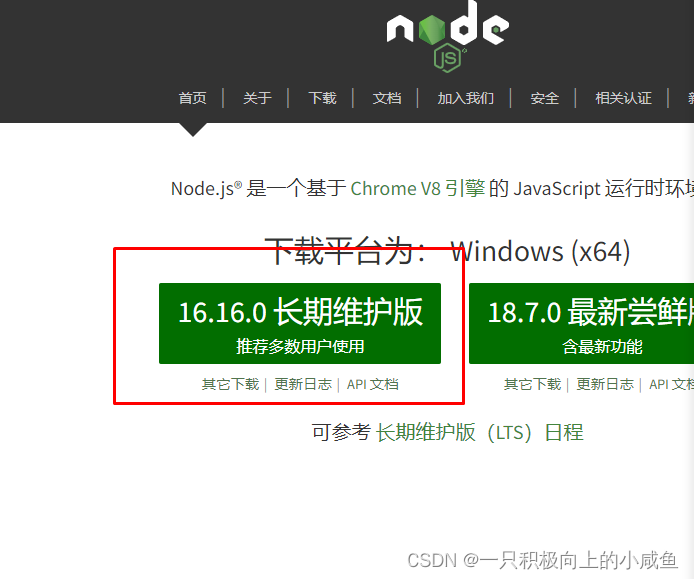
由于下载较慢,此处提供云盘链接:
链接:https://pan.baidu.com/s/1N3AdNu1Glo7MCyRFLWMPPQ
提取码:zkvy
(2)安装步骤
1、下载完成后,双击“node-v6.9.2-x64.msi”,开始安装Node.js

点击【Next】按钮
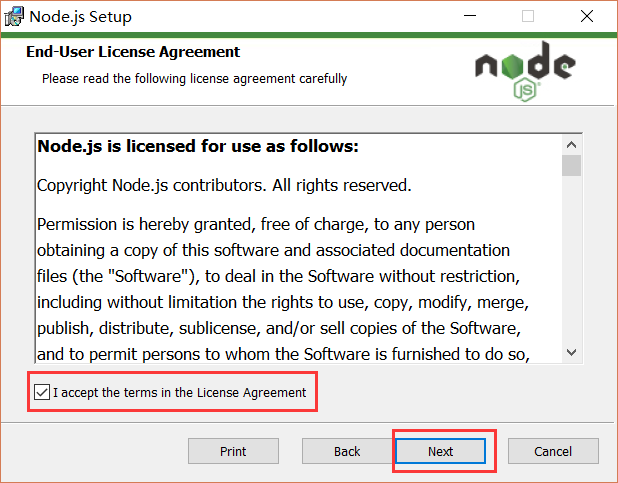
勾选复选框,点击【Next】按钮
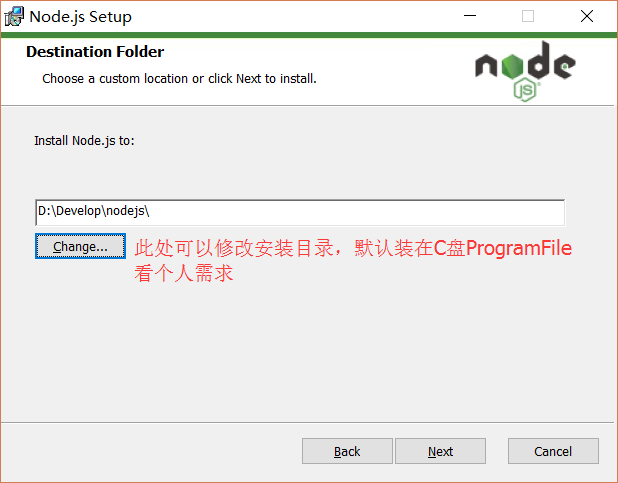
修改好目录后,点击【Next】按钮
安装完后点击【Finish】按钮完成安装
至此Node.js已经安装完成,可以先进行下简单的测试安装是否成功了,后面还要进行环境配置
在键盘按下【win+R】键,输入cmd,然后回车,打开cmd窗口

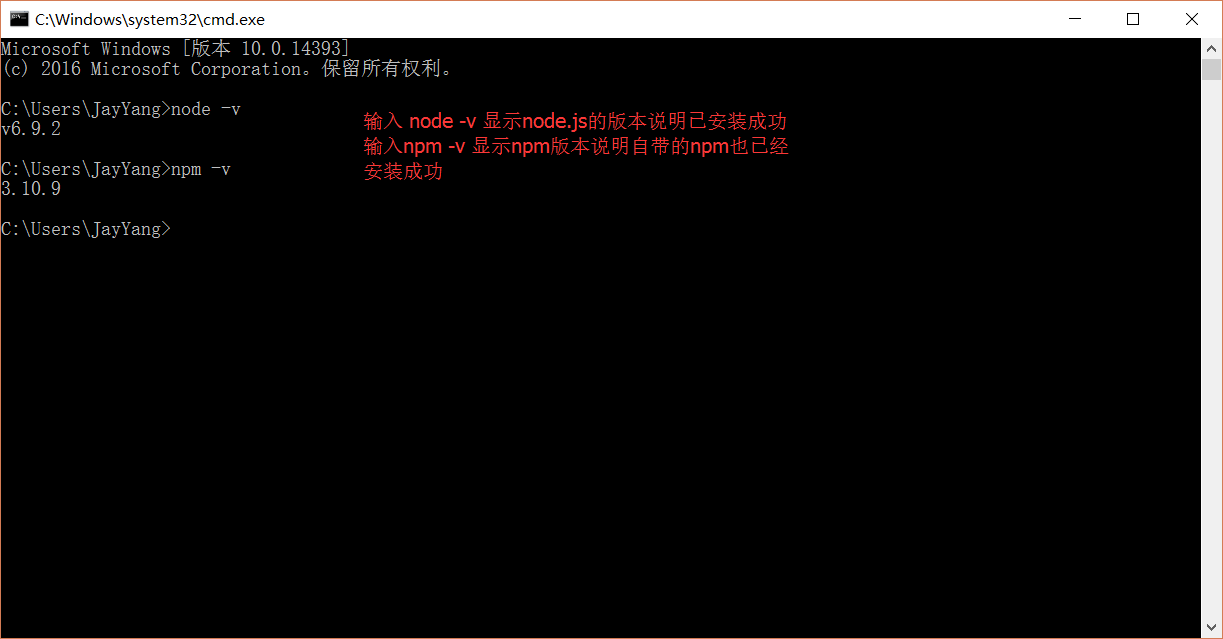
安装完后的目录如下图所示:

此处说明下:新版的Node.js已自带npm,安装Node.js时会一起安装,npm的作用就是对Node.js依赖的包进行管理,也可以理解为用来安装/卸载Node.js需要装的东西
如果仍有问题,参考Node.js安装及环境配置之Windows篇 - 刘奇云 - 博客园
注意:
1. 必须确定下载安装好nodejs再进行下一步配置picgo,
2.参考博客后文的配置对图床使用影响不大。
如需卸载,参考以下图片

2.3 Gitee设置
2.3.1在gitee上面创建一个仓库
有几点要求:
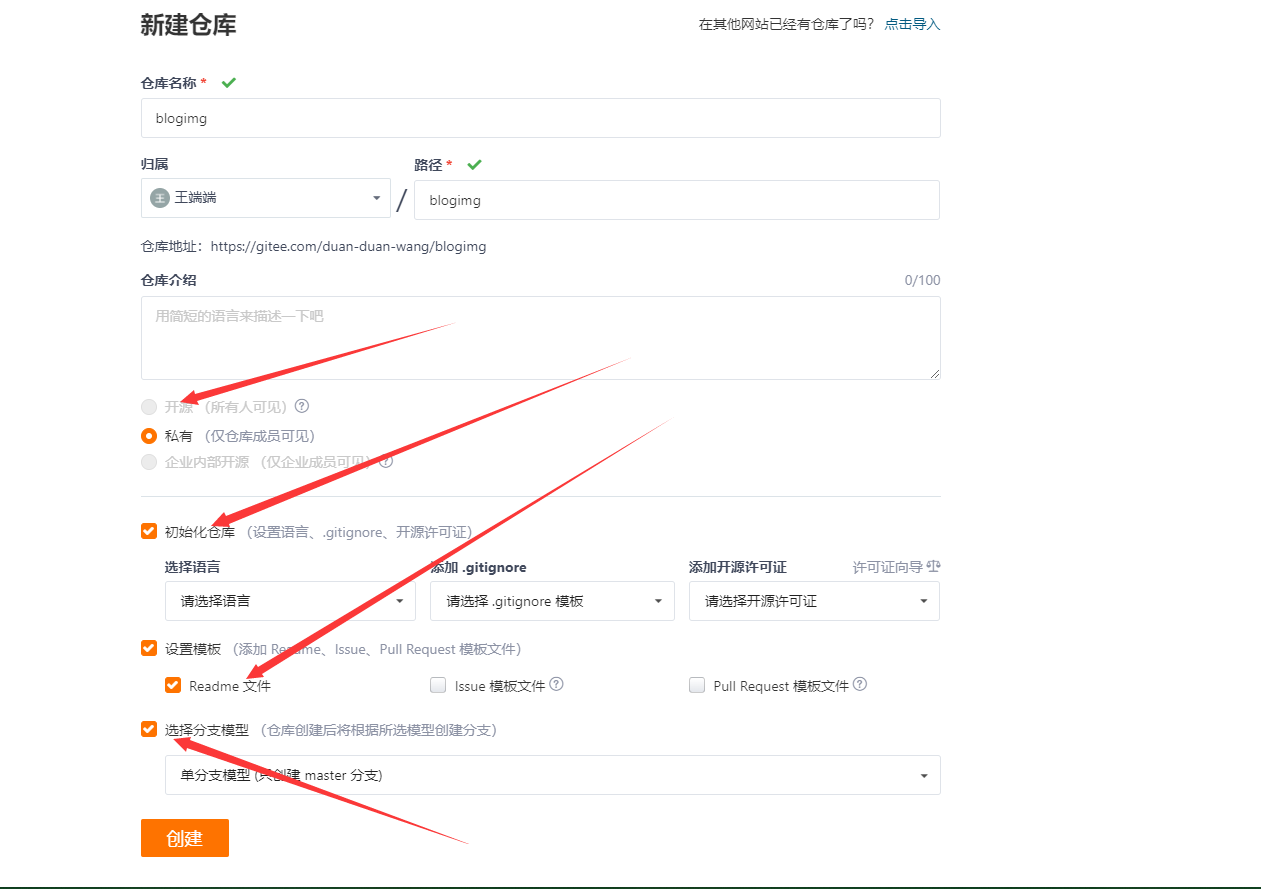
这个私有仓库,要在仓库管理中,调成开源的
2.4 整体配置
2.4.1 picgo软件配置
电脑上需要安装node.js才能安装插件,node.js安装见以上步骤
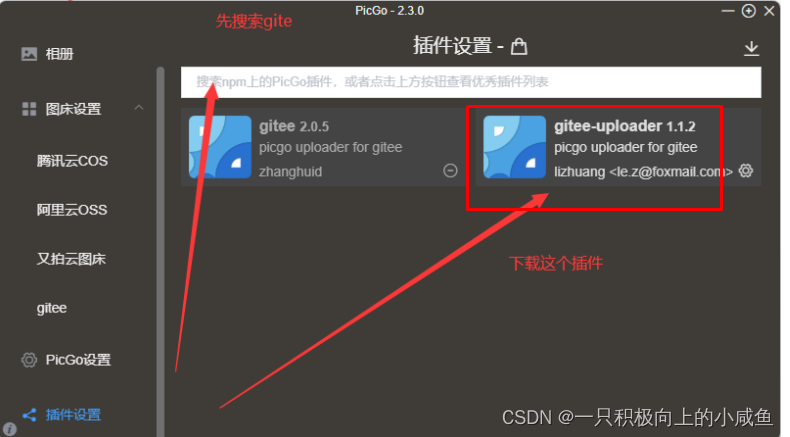
注意:
1. 此处插件安装只需安装右边的插件,不要安装左边的插件或者两个插件同时安装,不然会造成冲突。
2.4.2 图床设置

找到

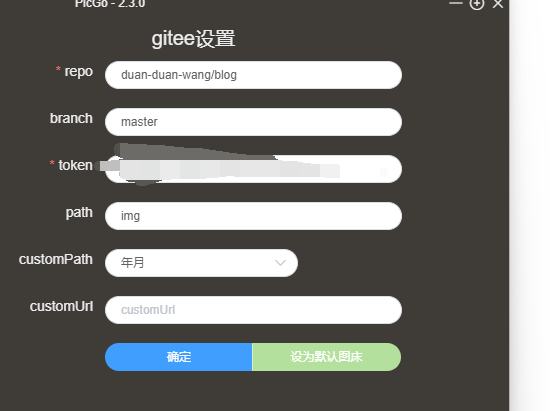
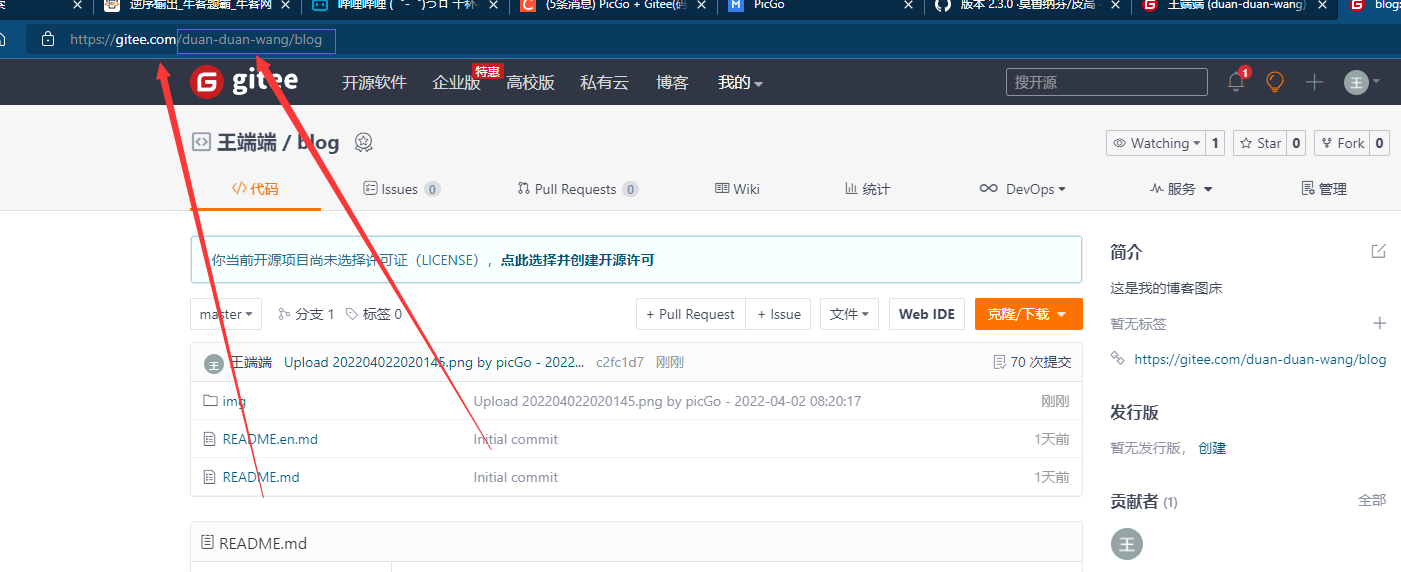
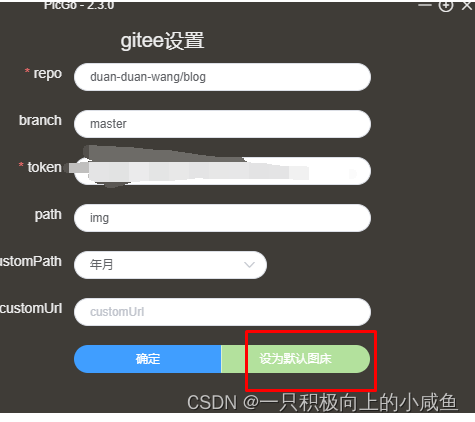
repo 是填写仓库主页上面的红框框里面的部分
注意:不能将仓库的网址粘贴到repo里。repo为用户名+仓库。若粘贴网址,后面会出现错误
branch填master
token是gitee私人令牌

勾选这些就行了
注意:令牌只能显示一次,及时进行复制 不然又要重新申请了
path就填img
下面的按照上面填年月就行
其他无要求了
最后,需要设置为默认图床
2.4.3 Typora配置
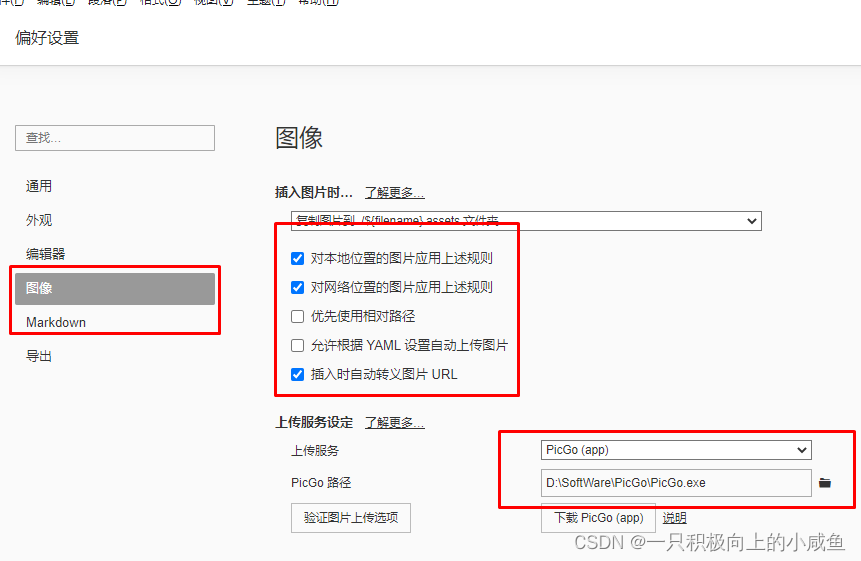
(1)设置
图像下的设置也可以全部打上勾
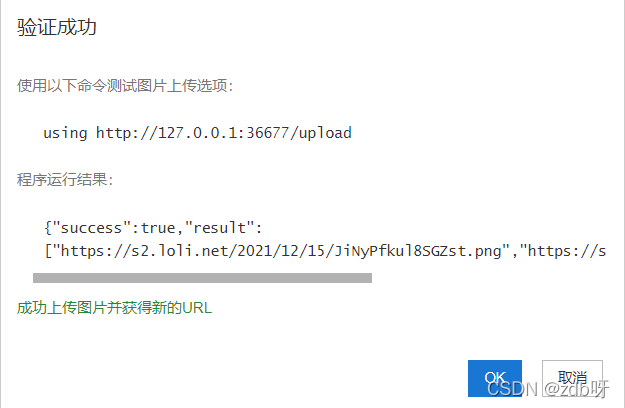
(2)
找到你picgo的安装路径,要找到那个exe文件的部分,再点击那个验证图片上传选项,成功以后就是完成配置了
三 失败问题总结
Picgo设置图床时候,出现:{“success”:false,“message”:“upload error”}
根据提示问题的log文件所在位置,查看失败信息
(1)情景1
Error: You must be logged in to use 的失败提示。
添加了gitee插件之后,要把它设为默认图床就可以解决了。不然你使用的是SM.MS图床。
(2)情景2
Error: Error in repo name
repo为用户名+仓库。需要自己检查一下是否填错
四 最终效果
在Typora中按如下方式进行
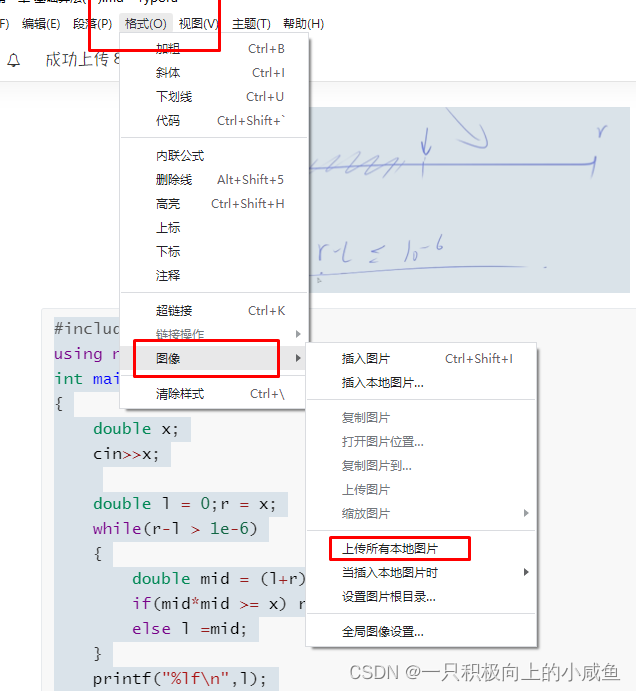

会有上传成功提示,相应的图片也变为GItee仓库中图床的网址。之后就可以在CSDN中粘贴图片了。
注意:
要上传某个文件的图片时,要按照以上方式上传本地所有图片。不要一个一个图片上传。不然会出现以下错误。
2021-08-19 19:59:43 [PicGo INFO] {"name":"StatusCodeError","statusCode":400,"message":"400 - \"{\\\"message\\\":\\\"A file with this name already exists\\\"}\"","error":"{\"message\":\"A file with this name already exists\"}","options":{"method":"POST","url":"https://gitee.com/api/v5/repos/Netceor/typora-image/contents/typora-icon2.png","headers":{"contentType":"application/json;charset=UTF-8","User-Agent":"PicGo"},出现上面错误时,需要比对上传出错的图片,然后再原库中删除相同图片后,再上传。较为麻烦
参考链接
1.外链图片转存失败,源站可能有防盗链机制---如何解决?手把手带你解决_四年过后。的博客-CSDN博客_外链图片转存失败
2. PicGo 安装及配置_长得很抽象的博客-CSDN博客_picgo
3. Node.js安装及环境配置之Windows篇 - 刘奇云 - 博客园
4. 【win10】Typora+PicGo+node+gitee配置图床_zdb呀的博客-CSDN博客
5. Typora+PicGo+Gitee自动上传图片_哔哩哔哩_bilibili

)


)


)

)

)


)

)
)

