文章目录
- Trie树
- 存储
- 并查集
- 常规例题
- 并查集维护多余信息
- 堆
- 性质
- 存储
- 基础操作
- down
- up
- 操作
- 例题
Trie树
Tire:高效地存储和查找字符串集合的数据结构
存储
如果没有就创建。
对单词结尾进行标记,表示以当前节点结尾的地方存在一个单词
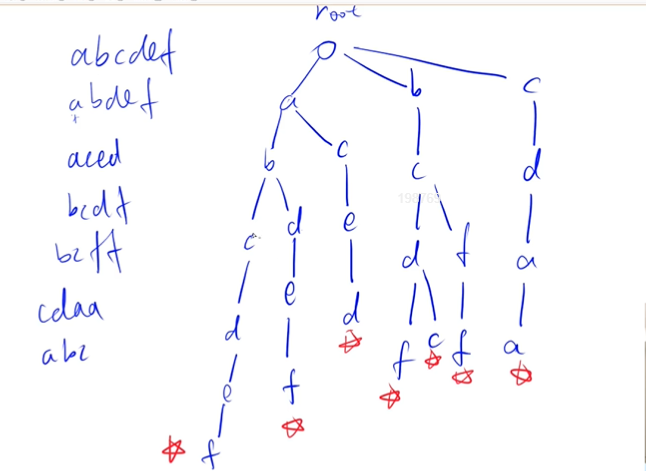
维护一个字符串集合,支持两种操作:I x 向集合中插入一个字符串 x;
Q x 询问一个字符串在集合中出现了多少次。
共有 N 个操作,输入的字符串总长度不超过 105,字符串仅包含小写英文字母。输入格式
第一行包含整数 N,表示操作数。接下来 N 行,每行包含一个操作指令,指令为 I x 或 Q x 中的一种。输出格式
对于每个询问指令 Q x,都要输出一个整数作为结果,表示 x 在集合中出现的次数。每个结果占一行。数据范围
1≤N≤2∗104
输入样例:
5
I abc
Q abc
Q ab
I ab
Q ab
输出样例:
1
0
1
#include <iostream>
using namespace std;const int N = 100010;
/*
下标为x的点,x的所有儿子存在son[x][i]中
cnt[x] 以x结尾的单词有多少个
idx 当前用到的哪一个下标 新插入一个节点++idx
idx: 0,1,2,3
*/
//第一个索引代表节点,26设置是因为最多有26个字母,每个节点最多有26个子节点
int son[N][26];
//单词结尾的标志,输入查询最多为N
int cnt[N];int idx; //代表节点的标号,即代表节点。每个节点的idx唯一,下标是0的点既是空节点又是根节点
char str[N];
void insert(char str[])
{int p = 0;for(int i = 0;str[i];i++) //CPP中字符串结尾是0 {//映射int u = str[i] - 'a';if(!son[p][u]) son[p][u] = ++idx;p = son[p][u];}//以该节点结尾的单词个数增加一个cnt[p]++;
}int query(char str[])
{int p = 0;for(int i = 0;str[i];i++){int u = str[i] - 'a';//不存在子节点if(!son[p][u]) return 0;p = son[p][u];}return cnt[p];
}int main()
{int n;scanf("%d",&n);while(n--){char op[2];scanf("%s%s",op,str);if(op[0] == 'I') insert(str);else printf("%d\n",query(str));}return 0;
}并查集
常规例题
作用:【学数据结构必须清楚该数据结构的用途】
- 将两个集合合并
- 询问两个元素是否在一个集合当中
每一个集合的编号是根节点的编号,每一个点存储他的父节点编号。

相关知识点与思路

合并两个集合:
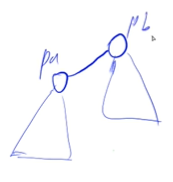
优化:
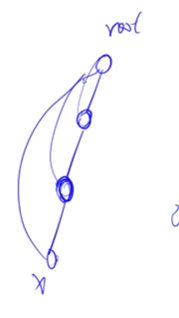
- 路径压缩:
求x的编号上复杂度为树的高度->找到根节点后所有节点均指向根节点。压缩后基本上就可实现O(1)复杂度
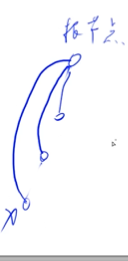
递归与回溯
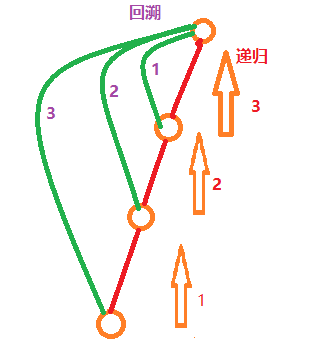
一共有 n 个数,编号是 1∼n,最开始每个数各自在一个集合中。现在要进行 m 个操作,操作共有两种:M a b,将编号为 a 和 b 的两个数所在的集合合并,如果两个数已经在同一个集合中,则忽略这个操作;
Q a b,询问编号为 a 和 b 的两个数是否在同一个集合中;
输入格式
第一行输入整数 n 和 m。接下来 m 行,每行包含一个操作指令,指令为 M a b 或 Q a b 中的一种。输出格式
对于每个询问指令 Q a b,都要输出一个结果,如果 a 和 b 在同一集合内,则输出 Yes,否则输出 No。每个结果占一行。数据范围
1≤n,m≤105
输入样例:
4 5
M 1 2
M 3 4
Q 1 2
Q 1 3
Q 3 4
输出样例:
Yes
No
Yes
#include <stdio.h>
using namespace std;
const int N =100010;
int n,m;
int p[N]; //father数组:存储每个节点的父节点是谁,初始时节点指向自己
//返回x所在集合的编号,添加路径压缩,最核心操作
int find(int x)
{//如果不是根节点,让他的父节点等于它的根节点if(p[x] != x) p[x] = find(p[x]);return p[x];
}int main()
{scanf("%d%d",&n,&m);//初始for(int i = 1;i<=n;i++) p[i] = i;while(m--){//有空格,所以用op[2]使用%c的话会默认接受空格,因此使用%schar op[2];int a,b ;scanf("%s%d%d",op,&a,&b);// print(op[0]);// puts(op[1]);//a的祖宗节点的父亲等于b的祖宗节点,让两个节点合并if(op[0] == 'M') p[find(a)] = find(b);else{if(find(a) == find(b) ) puts("Yes");else puts("No");}}return 0;
}
并查集维护多余信息
连通块:可以从A走到B
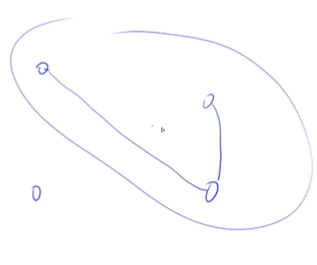
给定一个包含 n 个点(编号为 1∼n)的无向图,初始时图中没有边。现在要进行 m 个操作,操作共有三种:C a b,在点 a 和点 b 之间连一条边,a 和 b 可能相等;
Q1 a b,询问点 a 和点 b 是否在同一个连通块中,a 和 b 可能相等;
Q2 a,询问点 a 所在连通块中点的数量;
输入格式
第一行输入整数 n 和 m。接下来 m 行,每行包含一个操作指令,指令为 C a b,Q1 a b 或 Q2 a 中的一种。输出格式
对于每个询问指令 Q1 a b,如果 a 和 b 在同一个连通块中,则输出 Yes,否则输出 No。对于每个询问指令 Q2 a,输出一个整数表示点 a 所在连通块中点的数量每个结果占一行。数据范围
1≤n,m≤105
输入样例:
5 5
C 1 2
Q1 1 2
Q2 1
C 2 5
Q2 5
输出样例:
Yes
2
3
样例示意图

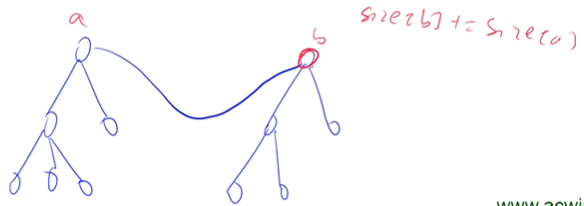
用集合代表连通块,在两个点添加边的作用为将两个集合合并。相对第一题,增加了一步为统计集合中点的数量
用size维护集合中点的数量,只有根节点有意义,添加集合时可以使用以下方法更新size
#include <stdio.h>
using namespace std;
const int N =100010;
int n,m;
int p[N];
int size[N];//size用于存储集合的大小,规定只有根节点的size有意义
int find(int x)
{if(p[x] != x) p[x] = find(p[x]);return p[x];
}int main()
{scanf("%d%d",&n,&m);for(int i = 1;i<=n;i++) {p[i] = i;//初始化,一开始每个集合中有一个点,size均为1size[i] = 1; }while(m--){char op[5];int a,b ;scanf("%s",op);if(op[0] == 'C') {scanf("%d%d",&a,&b);//特判:如果A与B已经在一个集合中,直接continue,后面操作不再进行if(find(a) == find(b)) continue;/*注意:以下两个语句的顺序不能颠倒:1.先进行size数组的更新2.再将两个集合合并如果先合并,会将一个集合的size覆盖导致没有一个集合没有意义*/size[find(b)] += size[find(a)];p[find(a)] = find(b); }else if(op[1] == '1'){scanf("%d%d",&a,&b);if(find(a) == find(b) ) puts("Yes");else puts("No");}else{scanf("%d",&a);printf("%d\n",size[find(a)]);}}return 0;
}
堆

性质
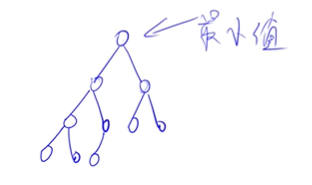
堆是一个完全二叉树:
- 除了最后一层节点以外,上面所有结点都是满的
- 最后一层节点从左到右排列
小根堆:每个节点都小于等于左右儿子,跟节点是整棵树的最小值
存储
用一维数组存储
下标从1开始,从0开始不太方便

基础操作
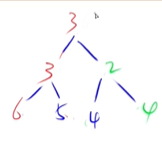
down
将节点向下移动
基本逻辑:如果把某一点值变大了,就需要将这个节点向下移动,越大的数越向下沉
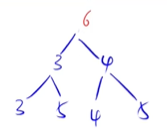
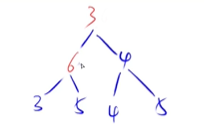
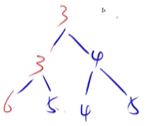
递归的过程
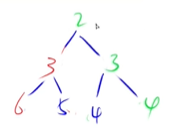
up
将节点向上移
基本逻辑:如果把某一点值变小了,就需要将这个节点向上移动,越小的数越向上浮
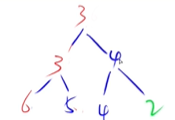
操作
-
插入一个数
在最后位置插入新的数,将这个数向上移动
heap[++size] = x; up(size); -
求集合中最小值
heap[1] -
删除最小
把最后一个元素覆盖堆顶元素,size–,再把堆顶down一遍
原因:
一维数组删除头结点比较困难,但删除尾节点比较方便[size–]
heap[1] = heap[size];size--;down(1) -
删除任意元素[类似删除最小]
heap值3种情况:不变;向下走;向上走
因此只会选择一个
heap[k] = heap[size];size--;down(k);up(k); -
修改任意值
heap[k] = x;down(k);up(k);s
时间复杂度:
求最小值:O(1)
插入与删除: O(logN)
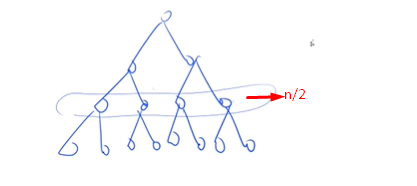
建立堆:
存在O(n)的建立堆的方式:从n/2开始down

例题
输入一个长度为 n 的整数数列,从小到大输出前 m 小的数。输入格式
第一行包含整数 n 和 m。第二行包含 n 个整数,表示整数数列。输出格式
共一行,包含 m 个整数,表示整数数列中前 m 小的数。数据范围
1≤m≤n≤105,
1≤数列中元素≤109
输入样例:
5 3
4 5 1 3 2
输出样例:
1 2 3
#include <stdio.h>
#include <algorithm>using namespace std;const int N = 100010;int n,m;
//h代表heap
int h[N],hsize;void down(int u)
{//t代表3个点中的最小值int t = u;if(u * 2 <= hsize && h[u*2] < h[t] ) t = u*2;if(u *2 + 1 <= hsize && h[u*2 + 1] < h[t]) t = u*2 +1;//最后,u存储的为三个点中最小值的节点编号if(u != t){swap(h[u],h[t]);//最后进行递归处理,当节点没有左右儿子时或者根节点比左右儿子小时,结束递归down(t);}
}//up只需要与父节点比较,不需要新加变量,down操作需要与左右儿子节点比较
void up(int u)
{//如果存在根节点[u>2]并且根节点的值大于儿子节点//终止条件为到头或者上面形成小队while(u / 2 && h[u/2] > h[u]){swap(h[u/2],h[u]);u /=2;}
}int main()
{scanf("%d%d",&n,&m);for(int i = 1;i <= n; i++) scanf("%d",&h[i]);//初始化hsize = n;// 索引从n/2 ~ 1可以使用这种方式;不是到0for(int i = n/2;i;i--) down(i);while(m--){printf("%d ",h[1]);h[1] = h[hsize];hsize--;down(1);}return 0;
}
维护一个集合,初始时集合为空,支持如下几种操作:I x,插入一个数 x;
PM,输出当前集合中的最小值;
DM,删除当前集合中的最小值(数据保证此时的最小值唯一);
D k,删除第 k 个插入的数;
C k x,修改第 k 个插入的数,将其变为 x;
现在要进行 N 次操作,对于所有第 2 个操作,输出当前集合的最小值。输入格式
第一行包含整数 N。接下来 N 行,每行包含一个操作指令,操作指令为 I x,PM,DM,D k 或 C k x 中的一种。输出格式
对于每个输出指令 PM,输出一个结果,表示当前集合中的最小值。每个结果占一行。数据范围
1≤N≤105
−109≤x≤109
数据保证合法。输入样例:
8
I -10
PM
I -10
D 1
C 2 8
I 6
PM
DM
输出样例:
-10
6
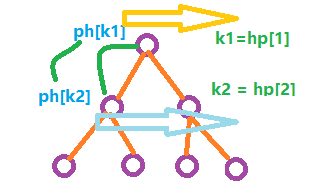
麻烦在于删除第k个插入的数,因此插入与删除时需要快速找到第k个数是啥,因此需要额外开两个数组存储[p–下标,h–堆]
| 名称 | 含义 | 作用 |
|---|---|---|
| ph[k] | 第k个插入数的在堆中下标是什么 | 寻找第k个插入的点 |
| hp[k] | 堆里的点是第几个插入的点 | 交换两个点后需要交换ph,需要知道点是第几个插入的。服务于ph数组 |
#include <stdio.h>
#include <algorithm>
#include <string.h>using namespace std;const int N = 100010;//h代表heap
int h[N],ph[N],hp[N],hsize;
char op[5];//交换不能是仅仅交换两个值,需要全新的交换操作,需要定义函数
void heap_swap(int a,int b)
{swap(ph[hp[a]],ph[hp[b]]);swap(hp[a],hp[b]);swap(h[a],h[b]);
}void down(int u)
{//t代表3个点中的最小值int t = u;if(u * 2 <= hsize && h[u*2] < h[t] ) t = u*2;if(u *2 + 1 <= hsize && h[u*2 + 1] < h[t]) t = u*2 +1;//最后,u存储的为三个点中最小值的节点编号if(u != t){heap_swap(u,t);//最后进行递归处理,当节点没有左右儿子时或者根节点比左右儿子小时,结束递归down(t);}
}//up只需要与父节点比较,不需要新加变量,down操作需要与左右儿子节点比较
void up(int u)
{//如果存在根节点[u>2]并且根节点的值大于儿子节点//终止条件为到头或者上面形成小队while(u / 2 && h[u/2] > h[u]){heap_swap(u/2,u);u /=2;}
}int main()
{int n,m = 0;scanf("%d",&n);while(n--){int k,x;scanf("%s",op);if(!strcmp(op,"I")){scanf("%d",&x);hsize++;m++;ph[m] = hsize;hp[hsize] = m;h[hsize] = x;up(hsize);}else if(!strcmp(op,"PM")) printf("%d\n",h[1]);else if(!strcmp(op,"DM")){heap_swap(1,hsize);hsize--;down(1);}else if(!strcmp(op,"D")){scanf("%d",&k);//用k来存储第k个点对应的下标,方便后面使用down(k),up(k);k = ph[k];heap_swap(k,hsize);hsize--;down(k),up(k);}//修改第k个插入的数else{scanf("%d%d",&k,&x);k = ph[k];h[k] = x;down(k),up(k);}}return 0;
}
此处为什么使用strcmp函数而不是像之前使用op[idx]进行字符串对比
因为输入为"I" DM" “PM” “D” “C” ,不容易根据字符串的某个索引区分不同的输入。因此采用更为精确的strcmp函数
/*
功能:函数strcmp的功能是比较两个字符串的大小。把字符串str1和str2从首字符开始逐个字符的进行比较,直到某个字符不相同或者其中一个字符串比较完毕才停止比较。字符的比较为ASCII码的比较。
输入:两个字符串
返回值:若字符串1大于字符串2,返回结果大于零;若字符串1小于字符串2,返回结果小于零;若字符串1等于字符串2,返回结果等于零
*/
int strcmp(char *str1,char * str2);

)

)


)

)
)









