package com.atguigu.tree;
public class BinaryTreeDemo { public static void main(String[] args) { //先需要创建一颗二叉树BinaryTree binaryTree = new BinaryTree ( ) ; //创建需要的节点HeroNode root = new HeroNode ( 1, "宋江" ) ; HeroNode node2 = new HeroNode ( 2, "吴用" ) ; HeroNode node3 = new HeroNode ( 3, "卢俊义" ) ; HeroNode node4 = new HeroNode ( 4, "林冲" ) ; HeroNode node5 = new HeroNode ( 5, "关胜" ) ; //说明,我们先手动创建二叉树,后面我们学习递归方式创建二叉树root.setLeft ( node2) ; root.setRight ( node3) ; node3.setRight ( node4) ; node3.setLeft ( node5) ; binaryTree.setRoot ( root) ; //测试System.out.println ( "前序遍历" ) ; //1,2,3,5,4binaryTree.preOrder ( ) ; System.out.println ( "中序遍历" ) ; //2,1,5,3,4binaryTree.infixOrder ( ) ; System.out.println ( "后序遍历" ) ; //2,5,4,3,1binaryTree.postOrder ( ) ; // //前序查找
// //前序查找的次数
// System.out.println ( "前序查找" ) ;
// HeroNode resNode = binaryTree.preOrderSearch ( 5) ;
// if(resNode!=null) {
// System.out.println ( "找到了,信息为no=" +resNode.getNo ( ) +",name=" +resNode.getName ( ) ) ;
// } else {
// System.out.println ( "没有找都no=" +15+"的英雄" ) ;
// } // //中序查找
// //中序查找的次数
// System.out.println ( "中序查找" ) ;
// HeroNode resNode = binaryTree.infixOrderSearch ( 5) ;
// if(resNode!=null) {
// System.out.println ( "找到了,信息为no=" +resNode.getNo ( ) +",name=" +resNode.getName ( ) ) ;
// } else {
// System.out.println ( "没有找都no=" +15+"的英雄" ) ;
// } //后序查找//后序查找的次数System.out.println ( "后序查找" ) ; HeroNode resNode = binaryTree.postOrderSearch ( 5) ;if(resNode!=null) { System.out.println ( "找到了,信息为no=" +resNode.getNo ( ) +",name=" +resNode.getName ( ) ) ; } else { System.out.println ( "没有找都no=" +15+"的英雄" ) ; } } } //定义BinaryTree二叉树
class BinaryTree { private HeroNode root;public void setRoot(HeroNode root) { this.root=root; } //前序遍历public void preOrder() { if(this.root!=null) { this.root.preOrder ( ) ; } else { System.out.println ( "二叉树为空,无法遍历" ) ; } } //中序遍历public void infixOrder() { if(this.root!=null) { this.root.infixOrder ( ) ; } else { System.out.println ( "二叉树为空,无法遍历" ) ; } } //后序遍历public void postOrder() { if(this.root!=null) { this.root.postOrder ( ) ; } else { System.out.println ( "二叉树为空,无法遍历" ) ; } } //前序查找public HeroNode preOrderSearch(int no) { if(root!=null) { return root.preOrderSearch ( no) ; } else { return null; } } //中序查找public HeroNode infixOrderSearch(int no) { if(root!=null) { return root.infixOrderSearch ( no) ; } else { return null; } } //后序查找public HeroNode postOrderSearch(int no) { if(root!=null) { return root.postOrderSearch ( no) ; } else { return null; } } } //先创建HeroNode节点
class HeroNode { private int no; private String name; private HeroNode left; //默认为nullprivate HeroNode right;//默认为nullpublic HeroNode(int no, String name) { super ( ) ; this.no = no; this.name = name; } public int getNo() { return no; } public void setNo(int no) { this.no = no; } public String getName() { return name; } public void setName(String name) { this.name = name; } public HeroNode getLeft() { return left; } public void setLeft(HeroNode left) { this.left = left; } public HeroNode getRight() { return right; } public void setRight(HeroNode right) { this.right = right; } @Overridepublic String toString() { return "HeroNode { " +"no=" + no +", name='" + name + '\'' +'}' ; } //编写前序遍历的方法public void preOrder() { System.out.println ( this) ;//先输出父节点//递归向左子树前序遍历if(this.left!=null) { this.left.preOrder ( ) ; } //递归向右子树前序遍历if(this.right!=null) { this.right.preOrder ( ) ; } } //中序遍历public void infixOrder() { //递归向左子树中序遍历if(this.left!=null) { this.left.infixOrder ( ) ; } System.out.println ( this) ;//输出父节点//递归向右子树中序遍历if(this.right!=null) { this.right.infixOrder ( ) ; } } //后序遍历public void postOrder() { //递归向左子树后序遍历if(this.left!=null) { this.left.postOrder ( ) ; } //递归向右子树后序遍历if(this.right!=null) { this.right.postOrder ( ) ; } System.out.println ( this) ; //输出父节点} //前序遍历查找public HeroNode preOrderSearch(int no) { System.out.println ( "进入前序查找" ) ;//比较当前节点是不是if(this.no==no) { return this; } //1.则判断当前节点的左子节点是否为空,如果不为空,则递归前序查找//2.如果左递归前序查找,找到节点,则返回HeroNode resNode=null;if(this.left!=null) { resNode=this.left.preOrderSearch ( no) ; } if(resNode!=null) { //说明我们左子树找到return resNode; } //1.左递归前序查找,找到节点,则返回,否则判断//2.当前的节点的右子节点是否为空,如果不空,则继续向右递归前序查找if(this.right!=null) { resNode=this.right.preOrderSearch ( no) ; } return resNode; } //中序遍历查找public HeroNode infixOrderSearch(int no) { //判断当前节点的左子节点是否为空,如果不为空,则递归中序查找HeroNode resNode=null;if(this.left!=null) { resNode=this.left.infixOrderSearch ( no) ; } if(resNode!=null) { //说明我们左子树找到return resNode; } System.out.println ( "进入中序查找" ) ;//如果找到,则返回,如果没有找到,就和当前节点比较,如果是则返回当前节点if(this.no==no) { return this; } //否则继续进行右递归的中序查找if(this.right!=null) { resNode=this.right.infixOrderSearch ( no) ; } return resNode; } //后序遍历查找public HeroNode postOrderSearch(int no) { //判断当前节点的左子节点是否为空,如果不为空,则递归中序查找HeroNode resNode=null;if(this.left!=null) { resNode=this.left.postOrderSearch ( no) ; } if(resNode!=null) { //说明我们左子树找到return resNode; } //如果左子树没有找到,则向右子树递归进行后序遍历查找if(this.right!=null) { resNode=this.right.postOrderSearch ( no) ; } if(resNode!=null) { //说明我们右子树找到return resNode; } System.out.println ( "进入后序遍历" ) ;//如果左右子树都没有找到,就比较当前节点是不是if(this.no==no) { return this; } return resNode; } } 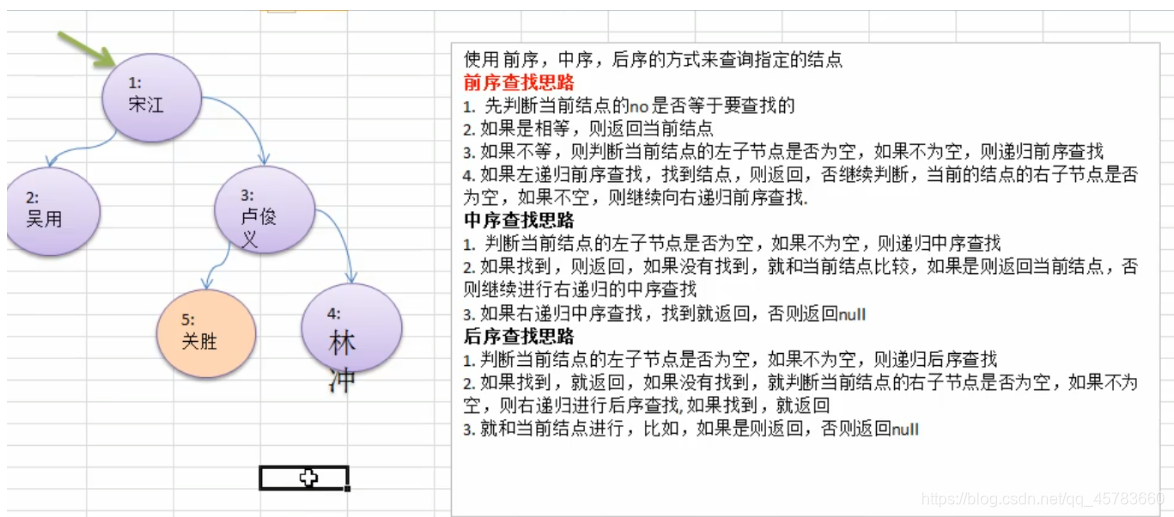

——BaseDao.java)






——IDeptDao.java)




——IEmpDao.java)



)

