若有需前后对比的数据，且要确定某种效果是否有统计依据，最常使用的是符号检验。通过举例可以很好地解释这个原理。

假设你在一家制药公司工作，想要确定一种新型减肥药是否有效。你找来八名志愿者服用这种减肥药长达几周的时间。观察八名实验对象在实验前后的体重变化。假设八名实验对象中有六名体重下降。有确凿的统计依据表明这种减肥药有效吗？

减肥药效是一个典型的符号检验示例，但此类检验也同样适用于许多 IT 和软件方案。假设你有 40 台 Web 服务器计算机，并应用了一个旨在提升性能的软件修补程序。测量应用此修补程序前后的响应时间。如果 32 台服务器的性能提升，2 台服务器的性能没有变化，6 台服务器的性能下降，能得出什么结论？

了解本文所述观点的最佳方式是查看图 1 中的演示程序。阅读完本文后，你将非常了解符号检验所能解决的问题类型、究竟该如何使用 C# 实现符号检验，以及该如何解读符号检验结果。本文展示了演示程序的所有源代码。还可以从本文随附的代码下载中获取完整的演示程序。

图 1：使用 C# 实现符号检验

演示程序设置了八对需前后对比的数据，旨在确定某减肥养生计划是否有效。从数据来看，六名实验对象的体重确实下降，而两名实验对象的体重上升。

演示程序计算的“无效”概率为 0.1445。如何解读此结果完全由你自己决定，例如，“数据表明减肥计划有效的迹象不充分 (p = 0.8555)。”

阅读本文的前提是，至少拥有中级编程技能，无需了解符号检验。演示代码用 C# 编写，依赖于 .NET System.Numerics 命名空间，因为需要使用 Microsoft .NET Framework 4（2010 年发布）或更高版本。

为了创建演示程序，我启动了 Visual Studio，并从“新建项目”菜单项中选择了“C# 控制台应用程序模板”。我将此项目命名为“SignTestUsingCSharp”。在将模板代码加载到编辑器窗口之后，我右键单击了解决方案资源管理器窗口中的 Program.cs 文件，并将此文件重命名为“SignTestProgram.cs”，然后允许 Visual Studio 为我重命名 Program 类。

接下来，我右键单击了项目名称，然后选择了“添加 | 引用”项。在“组件 | 框架”列表中，我选择了 System.Numerics 命名空间，然后单击了“确定”，将其添加到我的项目。在编辑器窗口顶部，我删除了所有 using 语句（引用顶级 System 命名空间的语句除外），然后添加了 using 语句来引用 System.Numerics 命名空间。

图 2 展示了程序的整体结构。为简单起见，程序采用的是严格意义上的静态方法，而不是面向对象编程 (OOP) 方法。DoCounts 和 ShowVector 方法是实用工具帮助程序。计算无效概率的工作是由 BinomRightTail 方法完成。BinomProb 和 Choose 方法是 BinomRightTail 的帮助程序。

using System;using System.Numerics;namespace SignTestUsingCSharp
{class SignTestProgram{static void Main(string[] args){Console.WriteLine("\nBegin Sign Test demo \n");// All calling statements go here      Console.WriteLine("\n\nEnd Sign Test demo \n");Console.ReadLine();}static int[] DoCounts(double[] before,double[] after) { . . }static void ShowVector(string pre, double[] v,int dec, string post) { . . }static double BinomProb(int k, int n,double p) { . . }static double BinomRightTail(int k, int n,double p) { . . }static BigInteger Choose(int n, int k) { . . }}
}

图 2：符号检验演示程序结构

在显示几条介绍信息之后，Main 方法设置并显示符号检验的演示数据：

double[] before = new double[] { 70, 80, 75, 85, 70, 75, 50, 60 };double[] after  = new double[] { 65, 78, 72, 87, 68, 74, 48, 63 };
Console.WriteLine("The weight data is: \n");
ShowVector("Before:  ", before, 0, "");
ShowVector("After :  ", after, 0, "\n");

在数据对超过约 30 个的非演示方案中，你会将数据存储在文本文件中，并编写用于读取和存储数据的帮助程序方法。使用平行数组是实现符号检验时最常用的方法。

接下来，演示使用 DoCounts 方法计算项目对数。如果体重下降，视为“成功项”，如果体重上升，视为“失败项”：

int[] counts = DoCounts(before, after);
Console.WriteLine("Num success = " + counts[2]);
Console.WriteLine("Num failure = " + counts[0]);

返回值是一个数组，其中存储单元 0 保存失败项数（体重上升），存储单元 1 保存无变化项数，存储单元 2 保存成功项数（体重下降）。

在计算机还没有普及的年代，计数是手动完成的，即在成功项旁边添加“+”号，在失败项旁边添加“-”号。这就是符号检验的命名由来。对于演示数据，手动方法如下所示：

Before:  70 80 75 85 70 75 50 60
After :  65 78 72 87 68 74 48 63+  +  +  -  +  +  +  -

请注意，符号检验不会考虑体重上升或下降的幅度。接下来，演示准备调用符号检验，如下所示：

int k = counts[2];int n = counts[0] + counts[2];
Console.WriteLine("k = " + k + " n = " + n + " p = 0.5");

变量 k 保存成功项数。变量 n 保存数据对总数。在此示例中，体重前后都有变化。在这种情况下，最常用的方法是不考虑无变化项。然而，在某些情况下，可能需要将无变化项添加为成功项或失败项。

例如，在减肥程序中，体重无变化很有可能会被视为失败。

Main 方法生成的结果如下：

double p_value = BinomRightTail(k, n, 0.5);
Console.WriteLine("\nProbability of 'no effect' is " + p_value.ToString("F4"));
Console.WriteLine("Probability of 'an effect' is " + (1 - p_value).ToString("F4"));

符号检验实际上是更为普遍的二项分布检验的具体示例。程序定义的函数 BinomRightTail 接受成功项数、数据对数以及概率值（在此示例中，为 0.5）。当二项分布检验使用 0.5 作为概率参数时，就是符号检验，我很快就会对此进行介绍。

符号检验采用二项分布，此分布反过来使用 Choose 函数。Choose(n, k) 函数返回从 n 个项中选择 k 个项的方法数。例如，Choose(5, 3) 返回从五个项中选择三个项时可以采用的方法数。假设这五个项为 (A, B, C, D, E)。从中选择三个项的方法有 10 种：

(A, B, C), (A, B, D), (A, B, E), (A, C, D), (A, C, E),
(A, D, E), (B, C, D), (B, C, E), (B, D, E), (C, D, E)

Choose 函数的定义为 Choose(n, k) = n! / [k! * (n-k)!]，其中“!”字符表示阶乘。那么，

Choose(5, 3) = 5! / (3! * 2!) = (5 * 4 * 3 * 2 * 1) / (3 * 2 * 1) *(2 * 1) = 120 / 12 = 10

实现 Choose 函数比较棘手，因为即使 n 和 k 值适中，返回值也可能会非常大。例如，

Choose(100, 25) = 242,519,269,720,337,121,015,504

为了能够返回非常大的值（在符号检验中可能会发生），演示程序在 System.Numerics 命名空间中使用 BigInteger 类型。Choose 的演示实现运用了两个数学技巧来提高效率。首先，事实证明，Choose(n, k) = Choose(n, n-k)。例如，

Choose(10, 7) = Choose(10, 3)

使用较小的 k 值，可以减少计算量。其次，Choose 还有另一种定义，以下示例最能解释：

Choose(10, 3) = (10 * 9 * 8) / (3 * 2 * 1)

也就是说，分母就是 k!，分子直接使用 n! 公式的前 k 项，很多项抵消掉了。综上，图 3 展示了 Choose 的演示实现。

static BigInteger Choose(int n, int k)
{if (n == k) return 1; // Required special case  int delta, iMax;if (k < n - k) { // Ex: Choose(100,3)    delta = n - k;iMax = k;}else { // Ex: Choose(100,97)    delta = k;iMax = n - k;}BigInteger ans = delta + 1;for (int i = 2; i <= iMax; ++i)ans = (ans * (delta + i)) / i;return ans;
}

图 3：Choose 函数

了解如何实现和解读符号检验的关键是了解二项分布。通过示例最能对此进行解释。

假设你有一个有偏硬币设计，投掷硬币出现正面的概率是 0.6，出现反面的概率是 0.4，并将出现正面定义为成功。如果投掷硬币 n = 8 次，二项分布为 n 个试验中恰好有 k 次成功的概率分布，其中每次试验的成功概率为 p（在此示例中为 0.6）。

在八次投掷中恰好出现八次正面和零次反面的概率就是连续出现八次正面的概率，即：

Pr(X = 8) = 0.6 * 0.6 * 0.6 * 0.6 * 0.6 * 0.6 * 0.6 * 0.6 = (0.6)^8 * (0.4)^0 = 0.0168

若要在八次投掷中恰好出现七次正面，可以在任意八次投掷中出现七次正面和一次反面。有八种组合：

Pr(X = 7) = Choose(8, 1) * [ (0.6)^7 * (0.4)^1 ] = 8 * 0.0280 * 0.4 = 0.0896

下面是在 n 个试验中恰好有 k 次成功的概率的常规公式，其中 p 是每次试验的成功概率：

P(X = k) = Choose(n, k) * p^k * (1-p)^n-k

在符号检验中，p 始终是 0.5，所以 1-p 也始终是 0.5，公式就简化为：

P(X = k) = Choose(n, k) * (0.5)^n

因此，对于演示数据，存在 n = 8 个试验（数据对）和 k = 6 次成功（体重下降），所以恰好六次成功的概率是：

P(X = 6) = Choose(8, 6) * (0.5)^8 = 28 * 0.0039 = 0.1094

图 4 展示了在八次试验中当 p = 0.5 时恰好零到八次成功对应的概率图。

实现返回二项分布概率的函数很简单：

static double BinomProb(int k, int n, double p)
{// Probability of k "successes" in n trials  // if p is prob of success on a single trial  BigInteger c = Choose(n, k);double left = Math.Pow(p, k);double right = Math.Pow(1.0 - p, n - k);return (double)c * left * right;
}

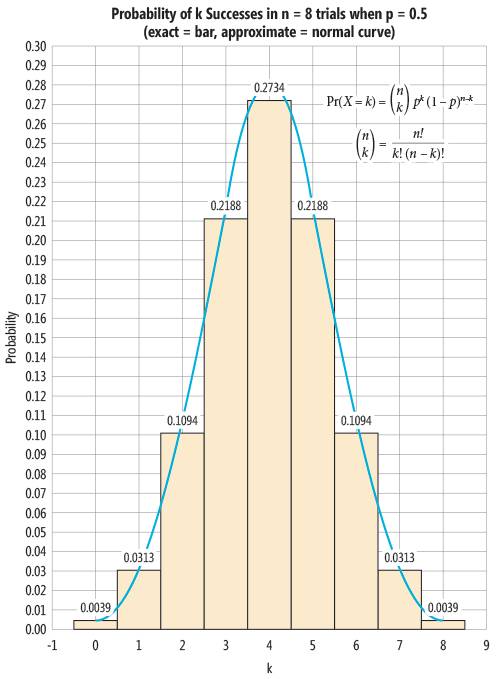
图 4：n = 8 和 p = 0.5 时的二项分布

演示定义了接受 p 作为参数的通用二项函数。另一种做法是，定义一个假设 p = 0.5 的版本并简化计算，如前所述。演示不含错误检查功能。例如，在生产环境中，可能需要确保 k <= n；k 和 n 都不是负数；p 介于 0.0 到 1.0 之间。

符号检验旨在计算无效概率。从概念上讲，这意味着前后值之间的任何差异纯粹是偶然。从数学上讲，这意味着上升或下降的概率为 0.5。

符号检验假设无效，然后计算在此假设下本该发生的成功项观测数的概率。对于八次试验中有六次成功（体重下降）的演示数据示例，计算的不是你可能会猜到的恰好六次成功的概率，而是六次以上成功的概率。这种思路相当微妙。

计算 k 次以上成功的概率有时被称为右尾检验。因此，若要实现符号检验，需要计算 k 次以上成功的概率，方法为计算恰好 k 次成功外加 K+1 次成功、K+2 次成功（依此类推）的概率。演示实现如下所示：

static double BinomRightTail(int k, int n, double p)
{// Probability of k or more successes in n trials  double sum = 0.0;for (int i = k; i <= n; ++i)sum += BinomProb(i, n, p);return sum;
}

完成符号检验只需用于统计成功次数和显示值的可选函数。演示将计数方法定义为：

static int[] DoCounts(double[] before, double[] after)
{int[] result = new int[3];for (int i = 0; i < before.Length; ++i) {if (after[i] > before[i])++result[0];  // Fail    else if (after[i] < before[i])++result[2]; // Success    else      ++result[0]; // Neither  }return result;
}

帮助程序显示方法为：

static void ShowVector(string pre, double[] v, int dec, string post)
{Console.Write(pre);for (int i = 0; i < v.Length; ++i)Console.Write(v[i].ToString("F" + dec) + " ");Console.WriteLine(post);
}

另一种设计是将成功失败计数与二项计算合并为一个更大的元方法。

应务必谨慎解读符号检验的结果。最好解读为“符号检验表明有效”，而不是“有效”。

示例问题被称为单侧或单尾检验。因为此示例涉及的是减肥实验，所以体重下降（成功项数）大于偶然值视为有效。

还可以执行双侧（亦称为“双尾”）符号检验。例如，假设要做的是某种止痛药的实验。在实验过程中，称量检验对象的实验前后体重。没有理由相信止痛药会影响体重。换句话说，体重下降或上升都可以视为有效。

符号检验最棘手的地方是要确保定义明确。由于每个问题都存在多重对称性，因此可能会产生混淆。可以将成功定义为后值增加或减少。

例如，在减肥示例中，将后值减少定义为成功。不过，如果数据表示的是学习前后某类考试的成绩，很可能会将后值增加定义为成功。

符号检验就是所谓的非参数统计检验示例。也就是说，在某种程度上，符号检验不对研究的数据分布作任何假设。可以使用所谓的配对 t 检验来取代符号检验。

然而，t 检验假设总体数据呈正态分布（高斯分布、钟形分布），用小数据集进行验证几乎是不可能的。正因为如此，我通常会在要调查需前后对比的数据时使用符号检验，而不是配对 t 检验。

Dr.James McCaffrey 供职于华盛顿地区雷蒙德市沃什湾的 Microsoft Research。他参与过多个 Microsoft 产品的工作，包括 Internet Explorer 和 Bing。Scripto可通过 jammc@microsoft.com 与 McCaffrey 取得联系。

衷心感谢 Microsoft 技术专家对本文的审阅： Chris Lee 和 Kirk Olynyk