从ThoughtWorks 2017技术雷达看微软技术

ThoughtWorks在每年都会出品两期技术雷达，这是一份关于技术趋势的报告，它比起一些我们能在市面上见到的其他各种技术行情和预测报告，更加具体，更具可操作性，因为它不仅涉及到新技术大趋势，比如云平台和大数据，更有细致到类库和工具的推介和评论，从而更容易落地。

Thoughtworks技术雷达

Thoughtworks技术雷达是以独特的形式记录ThoughtWorks技术顾问委员会的讨论结果，为从首席信息官到开发人员在内的各路利益相关方提供价值。这些内容只是简要的总结，但建议您探究这些技术以了解更多细节。这个雷达是图形性质的，把各种技术项目归类为技术、工具、平台和语言及框架四个象限。

技术雷达还进一步将这些技术分为四个环以反映ThoughtWorks目前对其的态度。这四个环是：

采用：强烈主张业界采用这些技术。
试验：值得追求。必须理解如何建立此功能。企业应该在风险可控的计划中尝试此技术。
评估：为了查明它将如何影响企业，值得作一番探究。
暂缓：谨慎研究。

在“采用”象限里的技术条目，只要场景恰当，就应该是技术开发者或决策者选择采纳的默认选项。“试验”环里，强调的是这项技术拥有足够的成功可能性，它们大多属于较新的技术领域，有较大发展潜力，只要在合适且风险可控的情况下，开发者即可尝试使用。此外，“评估”和“暂缓（proceed with caution）”象限则需要开发者对收益、风险、成熟度等条件评定下再谨慎使用。

技术雷达对于不同层级和水平的技术从业者，有可以从不同角度和分类进行解读的可能。不管你是个人开发者，对于新工具和技术有执着的追求，寄希望于从新工具和技术那里获取改进每日工作的灵感，或者你是技术领导者需要针对自己的系统做技术选型，以及对未来技术趋势的把握，技术雷达都会是一份很好的参考。

技术雷达在四个象限（技术，工具，平台，语言和框架）中，布满了大量由ThoughtWorks技术专家们发现的，可以极大改善开发效率和品质的条目。它们大多数会分布在每个象限的试验和评估区域。这些条目多具备创新和极客精神，可以很大程度上改善个人开发者的开发兴趣，保持对于新技术和技能的敏感度。

近日，ThoughtWorks发布了2017年第二期技术雷达，技术雷达具体参看https://www.thoughtworks.com/cn/radar。我自己合成了一张整个技术雷达的全貌如图所示：

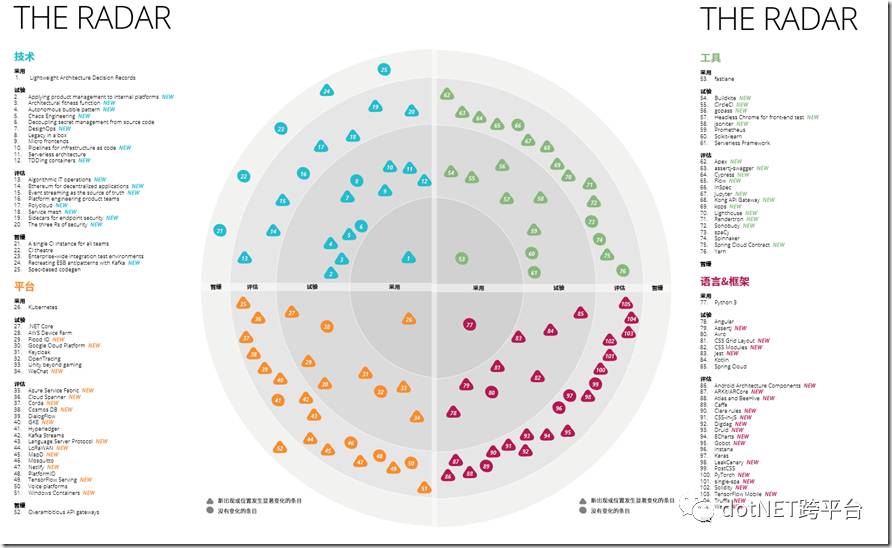
thoughtwork2017radar

在图中，自上次雷达发表以来新出现或发生显著变化的技术以三角形表示，而没有变化的技术则以圆形表示。每个象限的详细图表显示各技术发生的移动。这些评价可供企业作为采用某种技术的参考，对于各级技术人员来说，也具有一定的借鉴价值。而在本期技术雷达中，ThoughtWorks的技术顾问们又给我们带来了独特和前瞻性的技术视角，特别是微软技术方面，多项技术都是试验和评估，下面是从技术雷达中摘录的说明。

自我们上次在技术雷达中提到 Kubernetes 至今，它已经成为我们大部分客户将容器部署到服务器集群的默认解决方案。而能替代它的其他产品不但没有获得如此的客户认同度，甚至在某些场景中，我们的客户会将他们的“引擎” 都更换成 Kubernetes。Kubernetes已经成为主流公有云平台上的首选容器编排平台。这些主流公有云平台包括微软的 Azure 容器服务以及 Google Cloud。此外市面上还有很多好用的产品，来不断丰富快速扩大的Kubernetes 生态圈。与此同时，那些试图用一层抽象将Kubernetes隐藏起来的平台尚未成功地证明自己的价值。作为一个开源的跨平台软件开发框架，.NET Core被越来越多地运用到实际项目中。该框架令 .NET 应用能在 Windows、macOS 以及 Linux 进行开发和部署。.NET Standard 2.0 的发布增加了跨多个 .NET 平台的标准 API 的数量，这使得往 .NET Core 迁移的路径变得更为清晰。有关 .NET Core 对其上类库的支持性问题正在逐渐减少。一流的跨平台工具已经涌现出来，用于在非 Windows 平台上进行高效的开发工作。运用 Docker 镜像，能让 .NET Core 服务可以轻松地集成到容器环境中。其社区发展的积极方向以及来自我们实际项目的反馈，都表明 .NET Core 现在已经可以广泛地运用了。

Azure Service Fabric 是为微服务和容器打造的分布式系统平台。它不仅可以与诸如Kubernetes之类的容器编排工具相媲美，还可以支持老式的服务。它的使用方式花样繁多，既可以支持用指定编程语言编写的简单服务，也可以支持 Docker 容器，还可以支持基于 SDK 开发的各种服务。自几年之前发布以来，它不断增加更多功能，包括提供对 Linux 容器的支持。尽管 Kubernetes 已成为容器编排工具的主角，但 Service Fabric 可以作为 .NET 应用程序的首选。

云、devops、微服务、容器是现在这个发展阶段的软件形态。这样的形势下我们正在举办【深圳】大湾区第三次.NET技术交流会（网络直播），欢迎参加。

原文：http://www.cnblogs.com/shanyou/p/7940289.html

.NET社区新闻，深度好文，欢迎访问公众号文章汇总 http://www.csharpkit.com