正题

---

题目大意

一棵树，若干个点对，求不包括任何一个点对的路径数量。

---

解题思路

我们考虑将不合法的方案在坐标系上表示。

我们先只考虑一个点对$(x,y)$，若$x$和$y$没有祖先关系，则不合法的路径一个点在$x$的子树中，一个在$y$的子树中

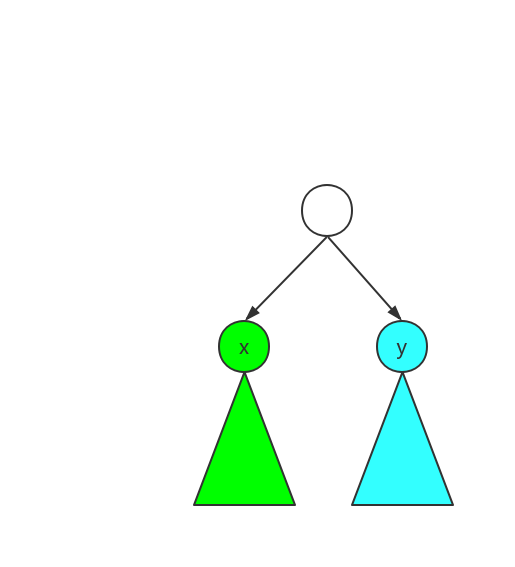
一个在绿色中选，一个在蓝色中选，也就是$si{z}_x\ast si{z}_y$个不合法方案

若$u$是$v$祖先则

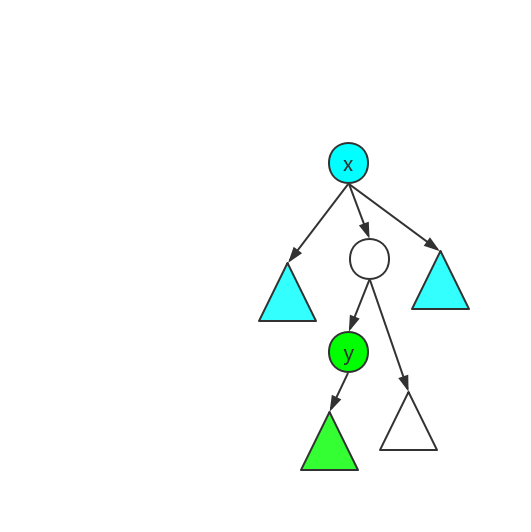
反之亦然

这时我们可以用倍增求出在$y$到$x$的路径中$x$的前一个点(也就是那个空白的圆)

那么一对点的情况就求好了，然后不是一对点时会有重复的。

我们先求一遍$dfs$序，然后用矩形$(x1,y1,x2,y1)$表是起点的$dfs$序在$x1\sim x2$这段范围，终点的$dfs$序在$y1\sim y2$这段范围是不可以选择的。

对于以上的第一种情况直接是一个矩形，然后第二种情况我们可以转换为两个矩形。

不过要注意的是要求$x1\le x2$且$y1\le y2$不然会有重复。

---

$code$

#include<cstdio>
#include<cstring>
#include<vector>
#include<cmath>
#include<algorithm>
using namespace std;
const int N=100100; 
int n,m,p[N][2],dfn[N],rfn[N],cnt;
int tot,ls[N],v[N],ed[N],num;
int f[N][30],dep[N],T;
long long ans;
vector<int> d[N];
struct treenode{int l,r,mark,val;
}t[N*8];
struct line_node{int x,Y1,y2,w;
}line[N*4];
void build(int k,int l,int r)
{t[k].l=l;t[k].r=r;if(l==r) return;int mid=(l+r)>>1;build(k*2,l,mid);build(k*2+1,mid+1,r);
}
void change(int k,int l,int r,int num)
{if(t[k].l==l&&t[k].r==r){t[k].mark+=num;if(t[k].mark)t[k].val=t[k].r+1-t[k].l;else if(l==r) t[k].val=0;else t[k].val=t[k*2].val+t[k*2+1].val;return;}int mid=(t[k].l+t[k].r)>>1;if(r<=mid) change(k*2,l,r,num);else if(l>mid) change(k*2+1,l,r,num);else change(k*2,l,mid,num),change(k*2+1,mid+1,r,num);if(t[k].mark)t[k].val=t[k].r+1-t[k].l;else t[k].val=t[k*2].val+t[k*2+1].val;
}
struct Edge_node{int to,next;
}a[N*2];
void addl(int x,int y)
{a[++tot].to=y;a[tot].next=ls[x];ls[x]=tot;
}
void dfs(int x,int fa)
{dfn[++cnt]=x;rfn[x]=cnt;f[x][0]=fa;for(int i=ls[x];i;i=a[i].next){int y=a[i].to;if(y==fa) continue;dep[y]=dep[x]+1;dfs(y,x);}ed[x]=cnt;
}
int LCA(int x,int y)
{for(int i=T;i>=0;i--)if(dep[f[y][i]]>dep[x]) y=f[y][i];return y;
}
void addc(int x1,int x2,int Y1,int y2)
{if(x1>x2) swap(x1,x2);if(Y1>Y1) swap(Y1,y2);line[++num]=(line_node){x1,Y1,y2,1};line[++num]=(line_node){x2+1,Y1,y2,-1};
}
bool cmp(line_node x,line_node y)
{return x.x<y.x;}
int main()
{freopen("tree.in","r",stdin);//freopen("tree.out","w",stdout);scanf("%d%d",&n,&m);for(int i=1;i<n;i++){int x,y;scanf("%d%d",&x,&y);addl(x,y);addl(y,x);}dfs(1,0);T=(int)(log(n)/log(2))+1;for (int j=1;j<=T;j++)for (int i=1;i<=n;i++)f[i][j]=f[f[i][j-1]][j-1];for(int i=1;i<=m;i++){int x,y;scanf("%d%d",&x,&y);if(rfn[x]>rfn[y]) swap(x,y);if(rfn[y]<=ed[x]&&rfn[y]>rfn[x]){int son=LCA(x,y);if(rfn[son]!=1) addc(1,rfn[son]-1,rfn[y],ed[y]);if(ed[son]!=n) addc(rfn[y],ed[y],ed[son]+1,n);}else addc(rfn[x],ed[x],rfn[y],ed[y]);}sort(line+1,line+1+num,cmp);build(1,1,n);int l=1;for(int i=1;i<=n;i++){while(l<=num&&line[l].x<=i){change(1,line[l].Y1,line[l].y2,line[l].w);l++;}ans+=t[1].val;}printf("%lld",(long long)n*(n-1)/2-ans);
}