2018 - 2019 SEERC 题解

比赛发出来太新了,网上根本就搜不到题解,补题补的太难受了.
在这里分享一篇我自己写的题解,也方便别人补题.

题目链接

http://codeforces.com/gym/101964/attachments/download/7814/seerc-2018.pdf

---

A.Numbers

不留坑,这题不会.

---

B.Broken Watch

题解

先考虑三个针长度各不一样的情况.

注意到需要对$n$分奇偶性进行讨论.

1. $n$为偶数的时候,固定$1$号针的位置,枚举$2$号针的位置,那么$3$号针的位置必然在$1,2$号针的反向延长线形成的扇形区域内(可与边界重合).
   并注意到当$1,2$号针反向的时候,$3$号针有$n-2$种取法.
   可以得到公式$n(1+2+...+\frac{n}{2}+n-2)$.
2. $n$为奇数的时候,固定$1$号针的位置枚举$2$号针的位置,那么$3$号针的位置必然在$1,2$号针反向延长线之间(不能与边界重合).
   可以得到公式$n(1+2+...+\lfloor \frac{n}{2}\rfloor )$

而当三根针有两根相同时,需要对答案除以$2!$,当三根全都相同时,需要对答案除以$3!$,这题就结束了.不明白为什么这个题比$C$题过得人少?

代码

org = input().split(" ")a = int(org[0])
b = int(org[1])
c = int(org[2])
n = int(org[3])len = 1if a == b and b == c:len = 6
elif a == b or b == c or a == c:len = 2mod = 2**64ans = 0
if n % 2 == 0:ans = (n*((n//2-1)*(n//2+2)+(n-2))//len )% mod
else:ans = (n*(n//2)*(n//2+1)//len) % modprint(ans)

---

C.Tree

题解

训练的时候想了一种树dp的做法,不太好调,幸好最后还是A掉了.赛后翻比别人代码发现还有一种很巧妙地方法,即枚举树的直径.两种方法我都简略说一下.

方法一.树dp

二分最大距离$M$,然后树$dp$来$check$可行性.

定义$dp[i][j]$表示以$i$为根的子树,选出来的黑点中距$i$节点距离不会超过$j$,所能选出最多的黑点个数.
并记lim=MIN{M−1−j,j−1}lim = MIN\{M-1-j,j-1\}lim=MIN{M−1−j,j−1}
那么转移就是:
假设$v_1,v_2,...,v_m$是$i$的儿子节点.

1. MIN1≤p≤m{dp[vp][j−1]+∑q!=pdp[vq][lim]}→dp[i][j]MIN_{1\le p \le m}\{dp[v_p][j-1] + \sum_{q != p}dp[v_q][lim]\} \rightarrow dp[i][j]MIN1≤p≤m​{dp[vp​][j−1]+∑q!=p​dp[vq​][lim]}→dp[i][j]

2. $dp[i][j-1]\to dp[i][j]$

最后只要看$dp[1][M]\ge k$.

时间复杂度?
$O(n^{3}log(n))$

方法二.枚举树的直径

先预处理出树上两点之间的距离(使用Floyd算法即可).

注意到将黑点取出之后会形成一颗虚树,并且两两之间最长的距离就是

然后我们考虑枚举这颗虚树的直径,假设是$(i,j)$,然后再枚举黑点,黑点进到虚树中一定不能使直径边长.所以就要要求$dis[i][k]\le dis[i][j]\&\&dis[k][j]\le dis[i][j]$.

时间复杂度$O(n^3)$

这个方法简单多了.

注意:不需要建虚树,说虚树主要是好描述.

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#define pr(x) std::cout << #x << ':' << x << std::endl
#define rep(i,a,b) for(int i = a;i <= b;++i)using namespace std;const int maxn = 105;
int n,m,val[maxn],dp[maxn][maxn];
vector<int> G[maxn];void dfs(int cur,int pre,int mid){for(int nx : G[cur]) if(nx != pre) dfs(nx,cur,mid);if(val[cur] == 1) dp[cur][0] = 1;for(int i = 1;i <= mid;i++){int limit = min(mid-1-i,i-1), sum = 0;if(limit >= 0) for(int nx : G[cur]) if(nx != pre){sum += dp[nx][limit];}dp[cur][i] = max(dp[cur][i],dp[cur][i-1]);for(int nx : G[cur]){if(nx == pre) continue;int tmp = dp[nx][i-1];if(limit >= 0) tmp += sum - dp[nx][limit];dp[cur][i] = max(dp[cur][i], val[cur]+tmp);}}
}
bool check(int mid){memset(dp,0,sizeof(dp));dfs(1,-1,mid);int f = 0;for(int i = 1;i <= n;++i)f |= dp[i][mid] >= m;return f;
}int main(){ios::sync_with_stdio(false);cin>>n>>m;for(int i = 1;i <= n;i++) cin>>val[i];for(int i = 0;i < n-1;i++){int u,v;cin>>u>>v;G[u].push_back(v);G[v].push_back(u);}int l = 0, r = n;while(r - l > 1){int mid = (l + r) >> 1;if(check(mid)) r = mid;else l = mid + 1;}if(check(l)) cout<<l<<endl;else cout<<r<<endl;return 0;
}

---

D.Space Station

题解

一道很神奇的题,需要先猜出结论,然后再进行树上背包.思路弄清楚了实现起来很简单.

简述一下题意:一颗$n$个结点的带权树,要求从$1$号点出发,遍历所有的边,然后回到$1$号点.途中可以最多使用$m$次技能,技能花费时间为$k$,功能是在任意两点中穿越.求最小代价.

我们先来发现一些规律性的东西.

1. 注意到一颗子树如果子树中包含的技能出发点和技能到达点共$p$个,如果$p$是偶数的时候,那么这颗子树根节点的父亲边一定要走两次(可以画图帮助理解一下)
2. 而如果$p$是奇数的话,那么子树根节点的父亲边只需要走一次就好了.(画图帮助理解)

这就很简单了.

定义$dp[i][j]$表示以$i$为根的子树,其子树中奇点个数为$j$,从$i$点出发遍历完$i$的子树再回到$i$点,所需要的最小代价.

那么转移方程就是

${\sum }_{p_1+p_2+...+p_m=j}(dp[v_i][p_i]+(![p_i\&1]+1)\ast c_i)\to dp[u][j]$

${\sum }_{p_1+p_2+...+p_m=j}(dp[v_i][p_i]+(![p_i\&1]+1)\ast c_i)\to dp[u][j+1]$

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#define pr(x) std::cout << #x << ':' << x << std::endl
#define rep(i,a,b) for(int i = a;i <= b;++i)
typedef std::pair<int,int> pii;
const int N = 1007; 
std::vector<pii> edge[N];
int dp[N][N],sz[N],tmp[N];
int n,m,k,T;
void upd(int &x,int y){if(y < x) x = y;
}
void dfs(int u,int fa) {sz[u] = 1;for(pii p : edge[u]) {int v = p.first,c = p.second;if(v == fa) continue;dfs(v,u);memset(tmp,0x3f,sizeof(tmp));for(int i = 0;i <= sz[u];++i) {for(int j = 0;j <= sz[v];++j) {if(i + j > 2*m) continue;if(j % 2 != 0) {upd(tmp[i+j],dp[u][i] + dp[v][j] + c);upd(tmp[i+j+1],dp[u][i] + dp[v][j] + c);}else {upd(tmp[i+j],dp[u][i] + dp[v][j] + 2*c);upd(tmp[i+j+1],dp[u][i] + dp[v][j] + 2*c);}}}sz[u] += sz[v];for(int i = 0;i <= sz[u];++i)dp[u][i] = tmp[i];}
}int main() {std::ios::sync_with_stdio(false);std::cin.tie(0);std::cin >> T;while(T--) {std::cin >> n >> m >> k;memset(dp,0,sizeof(dp));rep(i,1,n) edge[i].clear();rep(i,1,n-1) {int u,v,c;std::cin >> u >> v >> c;edge[u].push_back((pii){v,c});edge[v].push_back((pii){u,c});}dfs(1,0);int ans = 0x3f3f3f3f;for(int i = 0;i <= std::min(2*m,n);i += 2) upd(ans,dp[1][i]+(i/2*k));std::cout << ans << std::endl;}return 0;
}

---

E.Fisherman

题解

首先我们将钓鱼的人按照$x$坐标排个序，同时也记录一下他在答案里的顺序以便逆映射回去。
然后考虑每一条鱼能被哪些渔夫钓到，也就是考虑贡献。我们能够很简单地知道，一条鱼能够被钓到的地方在$x$轴上是一段连续的区间。当鱼的y坐标大于所给的线的长度时钓不到，否则记鱼线长度大于$y$坐标的长度$l-y=dl$，能够钓到鱼区间即为$[x-dl,x+dl]$。于是lower_bound和upper _bound找一下渔夫里面所对应的区间，然后区间加单点查询。区间加单点查询这个操作在代码里是使用了差分数组来维护的，最后算完之后把差分数组还原即可得到答案。

---

F.Min Max Convert

题解

大致的题意是给你两个长为$n$的数列$A,B$,然后你每次可以选择一段区间将区间覆盖成它的最大值或者是覆盖成它的最小值.要求输出一个长不超过$2n$的方案,将$A$数列变成$B$数列.

很明显的构造题.

我们首先要找一下规律以发现一些结论.

1. 一个区间最多通过两次操作可以将区间覆盖为区间中任意一个数.
   当$v$在区间边界上时,例如$v=a[l]$,将$[l,r]$覆盖为$v$的方法是:判断$a[l]$和$a[l+1]$的大小关系,如果$a[l]>a[l+1]$,那么就将$[l+1,r]$取最小值,再将$[l,r]$取最大值.
   当$v$在$[l,r]$中间时,可以将区间分成两段,分别操作.

2. 对于$B$数列的每个数,在$A$数列中都应该有一个数与它对应.并且这些对应关系不交叉.
   比如:
   $A:5,3,1,2,2,4,7,6,8,6$
   $B:1,1,2,4,4,7,7,8,8,8$
   那么对应关系是这样的:

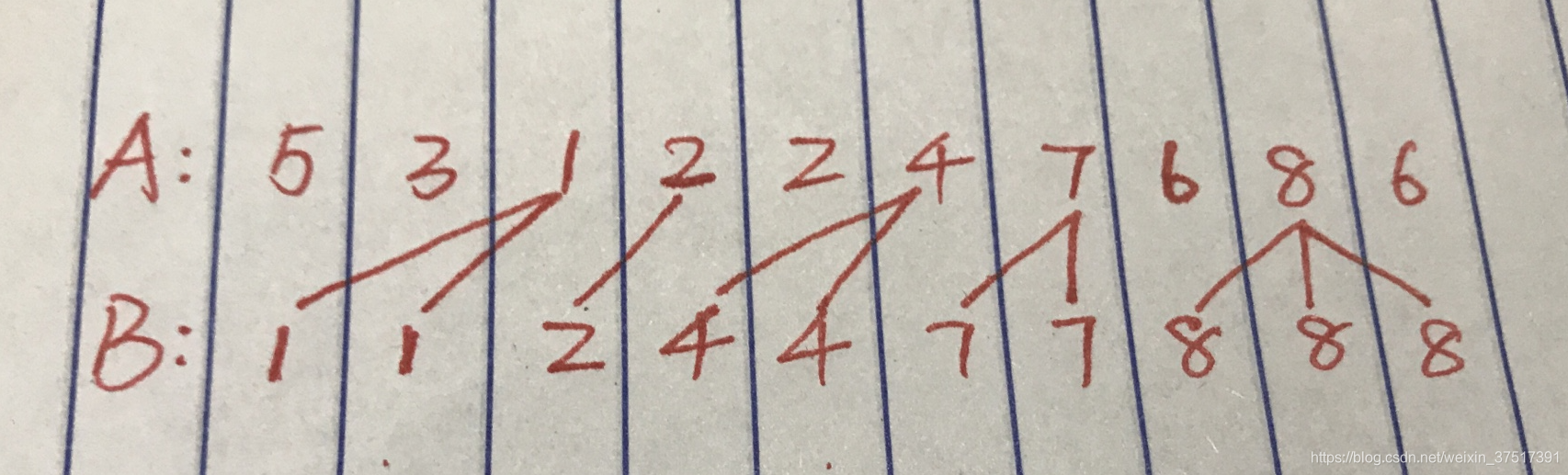
好难讲,直接看我代码吧.

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#define pr(x) std::cout << #x << ':' << x << std::endl
#define rep(i,a,b) for(int i = a;i <= b;++i)const int N = 100007;
int A[N],B[N],Loc[N];
char C[N<<1];int L[N<<1],R[N<<1];
int tot;
struct E{int b,e,x;
}es[N];
int etot = 0;
int n;
void Do(char c,int l,int r) {C[tot] = c;L[tot] = l;R[tot] = r;++tot;
}
int main() {scanf("%d",&n);rep(i,1,n) scanf("%d",&A[i]);rep(i,1,n) scanf("%d",&B[i]);int pos = 1;rep(i,1,n) {while(pos <= n && A[pos] != B[i]) pos ++;if(pos == n+1) return 0*puts("-1");Loc[i] = pos;	}int p = 1;rep(i,1,n) {if(Loc[i] != Loc[i+1]) {es[etot++] = (E){p,i,Loc[i]};p = i+1;}}for(int i = etot-1;i >= 0;--i) {if(es[i].x < es[i].b) {if(A[es[i].x] >= A[es[i].x+1]) {Do('m',es[i].x+1,es[i].e);Do('M',es[i].x,es[i].e);}if(A[es[i].x] < A[es[i].x+1]) {Do('M',es[i].x+1,es[i].e);Do('m',es[i].x,es[i].e);}}}rep(i,0,etot-1) {if(es[i].x > es[i].e) {if(A[es[i].x] <= A[es[i].x-1]) {Do('M',es[i].b,es[i].x-1);Do('m',es[i].b,es[i].x);}	if(A[es[i].x] > A[es[i].x-1]) {Do('m',es[i].b,es[i].x-1);Do('M',es[i].b,es[i].x);}}}rep(i,0,etot-1) {if(es[i].b <= es[i].x && es[i].x <= es[i].e) {if(es[i].x > es[i].b && A[es[i].x] >= A[es[i].x-1]) {Do('m',es[i].b,es[i].x-1);Do('M',es[i].b,es[i].x);}if(es[i].x > es[i].b && A[es[i].x] < A[es[i].x-1]) {Do('M',es[i].b,es[i].x-1);Do('m',es[i].b,es[i].x);}if(es[i].x < es[i].e && A[es[i].x] >= A[es[i].x+1]) {Do('m',es[i].x+1,es[i].e);Do('M',es[i].x,es[i].e);}if(es[i].x < es[i].e && A[es[i].x] < A[es[i].x+1]) {Do('M',es[i].x+1,es[i].e);Do('m',es[i].x,es[i].e);}}}std::cout << tot << std::endl;rep(i,0,tot-1) {printf("%c %d %d\n",C[i],L[i],R[i]);}return 0;
}

---

G.Matrix Queries

题解

队友$LNC$写的.

结论：我们称依题目给出的公式计算矩阵$A$的得分时递归处理到的矩阵均称为$A$的“子矩阵”，记这些矩阵中有$n$个为不“纯色”的矩阵，则矩阵A的得分为$4n+1$。

证明：
用数学归纳法：当$A$为$1\times 1$的矩阵时显然结论成立。
假设A为$2^k\times 2^k$的矩阵时结论成立，现证A为$2^{k+1}\times 2^{k+1}$矩阵时结论仍成立：

1. $A$纯色，则其得分为1，结论成立；
2. $A$不纯色，记其四个子矩阵的不纯色的子矩阵个数分别为$n_1$、$n_2$、$n_3$和$n_4$，则由假设它们的得分分别为$4n_1+1$、$4n_2+1$、$4n_3+1$和$4n_4+1$，A中不纯色的子矩阵个数为$n_1+n_2+n_3+n_4+1$，由定义A的得分$s=5+(n_1+n_2+n_3+n_4)=4(n_1+n_2+n_3+n_4+1)+1$，结论成立。

综上结论得证。

考虑到一个矩阵为纯色则这个矩阵的每行需修改相同奇偶次且每列也需修改相同奇偶次，统计有多少合法位置的连续$2^k$行与列修改的奇偶次数相同，相乘结果即$2^k\times 2^k$大小矩阵中纯色的个数，求反面即可。这些区间形成了线段树的结构，用线段树维护即可。

代码

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
const int maxn = (1<<20)+10;
ll seg[2][maxn*4],ans[2][21];void modify(int id,int o,int l,int r,int deep,int x){if(l == r){seg[id][o] ^= 1;return;}int mid = (l + r) >> 1;if(x <= mid) modify(id,o<<1,l,mid,deep+1,x);else modify(id,o<<1|1,mid+1,r,deep+1,x);if(seg[id][o] != -1) ans[id][deep]--;if(seg[id][o<<1] == seg[id][o<<1|1]) seg[id][o] = seg[id][o<<1];else seg[id][o] = -1;if(seg[id][o] != -1) ans[id][deep]++;
}
inline void read(int& x){char ch = getchar();x = 0;for(;ch < '0' || ch > '9';ch = getchar());for(;ch >= '0' && ch <= '9';ch = getchar()) x = x*10+(ch-'0');
}
inline void write(ll x){char ch = x%10+'0';if(x >= 10) write(x/10);putchar(ch);
}int main(){ios::sync_with_stdio(false);int n,m,sz;ll sum = 0;read(sz);read(m);n = (1 << sz);for(int i = 0;i < sz;i++){ans[0][i+1] = ans[1][i+1] = (1 << i);sum += (1ll << (i * 2)); }for(int i = 0;i < m;i++){int id, x;read(id);read(x);modify(id,1,1,n,1,x);ll tmp = 0;for(int i = 1;i <= sz;i++){tmp += 1ll*ans[0][i] * ans[1][i];}write(4ll * (sum - tmp) + 1);puts("");}return 0;
}

---

H.Modern Djinn

题解

留坑.

---

I.Inversion

题解

第一步,根据图恢原来的排列.

在得到原来的排列以后,我们从排列中挑选一些位置$(p_1,p_2,...p_m)$组成一个独立支配集.必然有$a[p_1]<a[p_2]<...<a[p_m]$,只有这样,集合里的点之间才没有边相连,并且还要满足条件即$[p_i,p_{i+1}]$之间的数要么大于$a[p_{i+1}]$,要么小于$a[i]$.

并且在排列中不可能存在$p_0<p_1并且a[p_0]<a[p_1]$,否则的话,它也应该存在于集合当中,应为它与集合中的所有点都无边相连.同理,不存在$p_{m+1}>p_m$,使得$a[p_{m+1}]>a[p_m]$.

如果$p<q且a[p]<a[q]且a[p,q]$之间的数不会存在介于$a[p]$与$a[q]$之间的数,就从$p$向$q$连边.

答案就是从入度为$0$的点,跑到出度为$0$的点的路径数之和.

拓扑序dp一下结束.

代码

#include <bits/stdc++.h>
using namespace std;typedef long long ll;
const int maxn = 105;
int a[maxn], in[maxn], cnt, x[maxn],n,m;
ll dp[maxn];
bool vis[maxn][maxn];
vector<int> G[maxn];ll dfs(int cur){if(dp[cur] != -1) return dp[cur];dp[cur] = 0;if(G[cur].size() == 0) dp[cur]++;for(int nx : G[cur]){dp[cur] += dfs(nx);}return dp[cur];
}int main(){ios::sync_with_stdio(false);cin>>n>>m;for(int i = 0;i < m;i++){int u,v;cin>>u>>v;vis[u][v] = vis[v][u] = 1;if(u < v) swap(u,v);G[u].push_back(v);in[v]++;}for(int i = 1;i <= n;i++){for(int j = i+1;j <= n;j++){if(vis[i][j]) continue;G[i].push_back(j);in[j]++;}}queue<int> q;for(int i = 1;i <= n;i++){if(in[i] == 0) q.push(i);}while(!q.empty()){int cur = q.front();q.pop();a[cur] = ++cnt;for(int nx : G[cur]){in[nx]--;if(in[nx] == 0) q.push(nx);}}memset(in,0,sizeof(in));for(int i = 1;i <= n;i++) G[i].clear();for(int i = 1;i <= n;i++){for(int j = i+1;j <= n;j++){if(a[i] > a[j]) continue;bool flag = true;for(int k = i + 1;k < j;k++)if(a[k] > a[i] && a[k] < a[j]) flag = false;if(flag){G[i].push_back(j);in[j]++;}}}ll ans = 0;memset(dp,-1,sizeof(dp));for(int i = 1;i <= n;i++) if(in[i] == 0) ans += dfs(i);cout<<ans<<endl;return 0;
}

---

J.Rabbit vs Turtle

题解

留坑

---

K.Points and Rectangles

题解

$cdq$分治的一道比较裸的题.

像这种能用二维线段树做的题(空间爆炸)都可以转换成离线cdq分治去解决.

每个点算作$1$个$event$.

每个矩形按照左边和右边拆成两个$event$,每个$event$包含上下边界.

我们考虑单独对点和矩形算贡献.

1. 对矩形算贡献:
   所有在该矩形前加的点都对矩形的左边$event$有$1$个负的影响,对矩形的右边$event$有$1$个正的贡献.
   维护一个树状数组,$i$位置的值代表目前存在的点$y$值为$i$的有多少个.
   那么对于每一个分治过程按照$event$的$x$从小到大的过程扫过来,遇见矩形左边$event$就将贡献减去$sum[down,up]$,遇见矩形右边$event$,就将贡献加上$sum[down,up]$.
   需要注意的一点是当多个$event$的$x$相同的情况下,我们按照矩形左边$event$,点$event$,矩形右边$event$ 顺序扫.

2. 对点算贡献.
   矩形的左边$event$对点会产生正的贡献,而矩形的右边$event$会对点产生负的贡献.
   还是按照$event$的$x$值从小到大的过程扫过来,遇见矩形左边$event$就将新树状数组的$down$位置$+1$,将$up+1$位置$-1$.
   遇见矩形右边$event$就将新树状数组的$down$位置$-1$,将$up+1$位置$+1$.
   在遇见点$event$时候,直接统计$sum[0,y]$的值就是包含这个点的矩形的贡献.
   需要注意的一点是当多个$event$的$x$相同的情况下,我们按照矩形左边$event$,点$event$,矩形右边$event$ 顺序扫.

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#define pr(x) std::cout << #x << ':' << x << std::endl
#define rep(i,a,b) for(int i = a;i <= b;++i)
#define int long long
int op[3] = {2,1,3};
const int N = 1e6;
struct event{int tp,id,x,up,down;event(int tp=0,int id=0,int x=0,int up=0,int down=0):tp(tp),id(id),x(x),up(up),down(down){}friend bool operator<(event &e1,event &e2) {return e1.x == e2.x ? (op[e1.tp] < op[e2.tp]) : (e1.x < e2.x);}
}es[N<<1];
int tot;int a[N],ans[N];
int bit1[N],bit2[N];
int ec = 0,q;event tmp[N<<1];int lowbit(int x) {return x & (-x);
}void add(int bit[],int pos,int x) {for(;pos < N;pos += lowbit(pos))bit[pos] += x;
}int sum(int bit[],int pos) {int res = 0;for(;pos;pos -= lowbit(pos)) {res += bit[pos];}return res;
}void clr(int bit[],int pos) {if(pos <= 0) return ;for(;pos < N;pos += lowbit(pos))bit[pos] = 0;
}void solve(int l,int r) {if(l == r) return ;int mid = (l + r) >> 1;solve(l,mid);solve(mid+1,r);std::vector<int> vec1,vec2;int s = 0,p = l,q = mid+1;while(p <= mid && q <= r) {if(es[p] < es[q]) {if(es[p].tp == 0) {add(bit1,es[p].up,1);vec1.push_back(es[p].up);}else if(es[p].tp == 1) {add(bit2,es[p].down,1);add(bit2,es[p].up+1,-1);vec2.push_back(es[p].down);vec2.push_back(es[p].up+1);}else if(es[p].tp == 2) {add(bit2,es[p].down,-1);add(bit2,es[p].up+1,1);vec2.push_back(es[p].down);vec2.push_back(es[p].up+1);}tmp[s++] = es[p++];}else {if(es[q].tp == 0) {ans[es[q].id] += sum(bit2,es[q].up);}else if(es[q].tp == 1) {ans[es[q].id] -= sum(bit1,es[q].up) - sum(bit1,es[q].down-1);}else if(es[q].tp == 2) {ans[es[q].id] += sum(bit1,es[q].up) - sum(bit1,es[q].down-1);}tmp[s++] = es[q++];}}while(p <= mid) tmp[s++] = es[p++];while(q <= r){if(es[q].tp == 0) {ans[es[q].id] += sum(bit2,es[q].up);}else if(es[q].tp == 1) {ans[es[q].id] -= sum(bit1,es[q].up) - sum(bit1,es[q].down-1);}else if(es[q].tp == 2)ans[es[q].id] += sum(bit1,es[q].up) - sum(bit1,es[q].down-1);tmp[s++] = es[q++];}for(int x : vec1) clr(bit1,x);for(int x : vec2) clr(bit2,x);rep(i,l,r) {es[i] = tmp[i-l];}
}signed main() {std::ios::sync_with_stdio(false);std::cin >> q;a[ec++] = 0;rep(i,1,q) {int tp;std::cin >> tp;if(tp == 1) {int x,y;std::cin >> x >> y;x+=2,y+=2;a[ec++] = x;a[ec++] = y;es[tot++] = event(0,i,x,y,0);}	else if(tp == 2) {int _a,_b,_c,_d;std::cin >> _a >> _b >> _c >> _d;_a+=2,_b+=2,_c+=2,_d+=2;a[ec++] = _a;a[ec++] = _b;a[ec++] = _c;a[ec++] = _d;es[tot++] = event(1,i,_a,_d,_b);es[tot++] = event(2,i,_c,_d,_b);}}	std::sort(a,a+ec);ec = std::unique(a,a+ec)-a;for(int i = 0;i < tot;++i) {es[i].x = std::lower_bound(a,a+ec,es[i].x)-a;es[i].up = std::lower_bound(a,a+ec,es[i].up)-a;es[i].down = std::lower_bound(a,a+ec,es[i].down)-a;}solve(0,tot-1);rep(i,1,q) {ans[i] += ans[i-1];std::cout << ans[i] << std::endl;}return 0;
}