三元环计数

问题

给出一张n个点m条边的无向图，问图中有多少个三元组{ u , v , w } ，满足图中存在 { (u,v) , (v,w) , (w,u) } 三条边。

求解

Step1 定向

将所有点按 度数 从小到大排序，如果度数相同按 点编号 从小到大排序，u的排名记作 $rn{k}_u$。

将这张图转化为有向图：对于一条无向边 x − y ，若 $rn{k}_x>rn{k}_y$，那么就将这条无向边变成 x → y 。反之则反之。

这样转化后，这张图一定是 有向无环图 。

证明：

使用反证法，假设有一个环：$a\to b\to c\to a$，
那么有（设 x 的度数为 $d_x$）：
$d_a\ge d_b\ge d_c\ge d_a$，要使该不等式成立，当且仅当满足 $d_a=d_b=d_c=d_a$。

设 x 的编号为 $i{d}_x$，那么有：$i{d}_a>i{d}_b>i{d}_c>i{d}_a$，即 $i{d}_a>i{d}_a>i{d}_a>i{d}_a$，该式子不成立，故假设不成立，证毕。

Step2 暴力枚举

枚举一个点 u 和它的所有出边到的点 v 并标记，再枚举 v 的出边到的点 w，如果 w 也有标记则表示找到了一个三元环

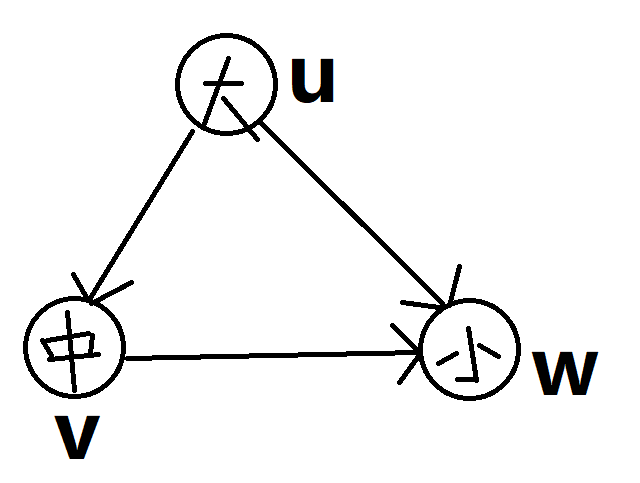
这样，每个三元环只会在 u 被统计一次（$rn{k}_u$在三元环中是最大的）

Code

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e5+5;
const int M=2e5+5;
struct Edge{int v,nxt;
}edge[M<<1];
int n,m,head[N],cnt,a[M],b[M];
int d[N],ans,mark[N];
void add_edge(int u,int v){edge[++cnt].v=v;edge[cnt].nxt=head[u];head[u]=cnt;
} 
bool cmp(int a,int b){if(d[a]==d[b]) return a>b;return d[a]>d[b];
}
int main(){scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){scanf("%d%d",&a[i],&b[i]);d[a[i]]++;d[b[i]]++;}for(int i=1;i<=m;i++){if(d[a[i]]>d[b[i]]||(d[a[i]]==d[b[i]]&&a[i]>b[i]))add_edge(a[i],b[i]);else add_edge(b[i],a[i]);}for(int u=1;u<=n;u++){for(int i=head[u];i;i=edge[i].nxt) mark[edge[i].v]=u;for(int i=head[u];i;i=edge[i].nxt){int v=edge[i].v;for(int j=head[v];j;j=edge[j].nxt){int w=edge[j].v;if(mark[w]==u) ans++;}}}printf("%d\n",ans);return 0;
} 

时间复杂度

考虑每一条边被遍历的次数：对于一条边 $x\to y$，他被遍历的次数为 $i{n}_x$ 。（$i{n}_x$表示 x 的入度），那么总的时间复杂度就是每一条边的 $i{n}_x$ 之和。

又可以发现，$i{n}_x$ 的上限就是 $\sqrt{m}$，因为要求每个连向 x 的点的度都大于 $i{n}_x$ ，也就是说，有 $i{n}_x$ 个点的度数大于$i{n}_x$，这样就至少需要 $i{n}_x^2$ 条边，所以 $i{n}_x^2\le m\Rightarrow i{n}_x\le \sqrt{m}$

所以总时间复杂度 $O(m\sqrt{m})$

四元环计数

问题

给出一张n个点m条边的无向图，问图中有多少个四元组{ u , v , w ，x } ，满足图中存在 { (u,v) , (v,w) , (w,x)，(x,u) } 四条边。

求解

Step1 定向

同三元组计数

Step2 暴力枚举

枚举一个点 u 和它的所有 出边 到的点 v ，然后枚举 v 的 无向边 到的点 w，其中要求 $rn{k}_u>rn{k}_w$

每访问到一个 w 给答案加上 w 的标记，并给 w 的标记加 1

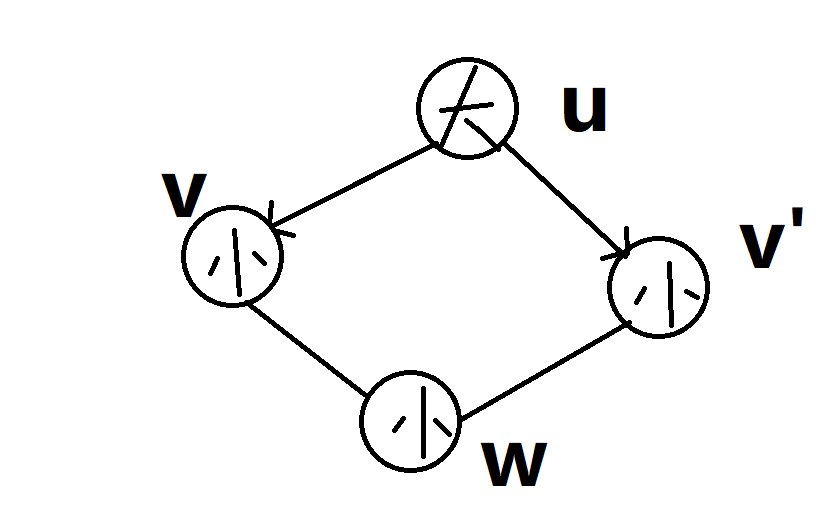
这样，每个四元环只会在 u 被统计一次（$rn{k}_u$在四元环中是最大的）

Code

#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e5+5;
const int M=2e5+5;
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}return x*f;
}
struct Edge{int v,nxt;
}edge[M<<1],e[M<<1];
int n,m,head[N],cnt,hd[N],ct,a[M],b[M];
int d[N],mark[N],tmp[N];
long long ans;
void add_edge(int u,int v){edge[++cnt].v=v;edge[cnt].nxt=head[u];head[u]=cnt;
} 
void add_e(int u,int v){e[++ct].v=v;e[ct].nxt=hd[u];hd[u]=ct;
}
bool cmp(int a,int b){if(d[a]==d[b]) return a>b;return d[a]>d[b];
}
int main(){n=read();m=read();for(register int i=1;i<=m;i++){a[i]=read();b[i]=read();d[a[i]]++;d[b[i]]++;add_e(a[i],b[i]);add_e(b[i],a[i]);}for(register int i=1;i<=m;i++){if(d[a[i]]>d[b[i]]||(d[a[i]]==d[b[i]]&&a[i]>b[i]))add_edge(a[i],b[i]);elseadd_edge(b[i],a[i]);}ans=0;for(register int u=1;u<=n;u++){for(register int i=head[u];i;i=edge[i].nxt){int v=edge[i].v;for(register int j=hd[v];j;j=e[j].nxt){int w=e[j].v;if(d[u]>d[w]||(d[u]==d[w]&&u>w)){ans+=1ll*tmp[w];tmp[w]++;}}}for(register int i=head[u];i;i=edge[i].nxt){int v=edge[i].v;for(register int j=hd[v];j;j=e[j].nxt){int w=e[j].v;if(d[u]>d[w]||(d[u]==d[w]&&u>w)) tmp[w]=0;}}}printf("%lld\n",ans);return 0;
}

时间复杂度

$O(m\sqrt{m})$

证明（自己想的，不保证对）：

对于边$x-y$，假设它定向后为 $x\to y$，
那么作为无向边它被遍历 $i{n}_x+i{n}_y$ 次，作为有向边被遍历 $i{n}_x$ 次，总过被遍历 $2i{n}_x+i{n}_y$ 次

总复杂度仍是 $O(m\sqrt{m})$