2020牛客暑期多校训练营（第一场）

A B-Suffix Array

B Infinite Tree

C Domino

D Quadratic Form

E Counting Spanning Trees

F Infinite String Comparision

题意：

两个字符串A和B，对AAAA…和BBBB…(字符串A和B无限重复）进行比较，输出 > = <

题解：

方法一：
字符串a和b从第一位开始比较，当比到其中最后一位时再跳转到第一位继续。那什么时候算等于呢，我一开始想的是a和b的最小公倍数，这样会超时，我们其实只需比较较长字符串的两倍即可。因为如果两个字符串不相等，那么在较长字符串的两倍范围内必将可以必出大小关系
方法二：
很简单，比较a+b和b+a的大小关系，直接输出
如果a和b相等，那么a+b肯定==b+a,否则两者肯定能必出大小

代码：

方法一：

#include <iostream>
#include <math.h>
#include <stdlib.h>
#include <cstring>
#include <stdio.h>
#include <queue>
#include <algorithm>
#include <vector>
#include <map>
#include <set>
#include <string>#define MAX 1000010using namespace std;typedef long long ll;char a[MAX];
char b[MAX];int main(){while(~scanf("%s %s",a,b)){int la=strlen(a);int lb=strlen(b);ll l=max(la,lb)*2;int ia=0,ib=0;int flag=0;for(ll i=0;i<l;i++){if(a[ia]>b[ib]){printf(">\n");flag=1;break;}else if(a[ia]<b[ib]){printf("<\n");flag=-1;break;}else {ia++;ib++;if(ia==la)ia=0;if(ib==lb)ib=0;}}if(flag==0){printf("=\n");}}return 0;
}

方法二：

#include <cassert>
#include <cmath>
#include <cstdint>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <bitset>
#include <complex>
#include <deque>
#include <functional>
#include <iostream>
#include <map>
#include <numeric>
#include <queue>
#include <set>
#include <sstream>
#include <string>
#include <unordered_map>
#include <unordered_set>
#include <utility>
#include <vector>using namespace std;using Int = long long;template <class T1, class T2> ostream &operator<<(ostream &os, const pair<T1, T2> &a) { return os << "(" << a.first << ", " << a.second << ")"; };
template <class T> void pv(T a, T b) { for (T i = a; i != b; ++i) cerr << *i << " "; cerr << endl; }
template <class T> bool chmin(T &t, const T &f) { if (t > f) { t = f; return true; } return false; }
template <class T> bool chmax(T &t, const T &f) { if (t < f) { t = f; return true; } return false; }char S[100010];
char T[100010];int main() {for (; ~scanf("%s%s", S, T); ) {const string s = S;const string t = T;const string st = s + t;const string ts = t + s;puts((st < ts) ? "<" : (st > ts) ? ">" : "=");}return 0;
}

G BaXianGuoHai, GeXianShenTong

H Minimum-cost Flow

I 1 or 2

J Easy Integration

题意

对于一个n，求出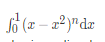的值，结果可以写成p/q的形式，最后输出 (p⋅q ⁻¹ )mod998244353 的值

题解

沃利斯公式

直接有公式，带入计算就行

代码

#include<bits/stdc++.h>
using namespace std;const int manx=2e6+5;
const int N=1e3+5;
const int mod=998244353;ll dp[manx],n;
ll poww(ll a, ll b){ll ans=1;while(b){if(b&1) ans=ans*a%mod;a=a*a%mod;b>>=1;}return ans%mod;
}
ll inv(ll x){return poww(x,mod-2);
}
int main()
{dp[1]=1;for(int i=2;i<=2000005;i++) dp[i]=dp[i-1]*i%mod;while(cin>>n){ll ans=dp[n]*dp[n]%mod*inv(dp[2*n+1])%mod;cout<<ans<<endl;}return 0;
}