Boundary（2020多校第二场B）

题意：

坐标平面有n个点（不与原点（0,0）重复）,现考虑一个圆，（0,0）点在圆的边界，问这个圆的边界上最多能有多少其他的点（不含原点）？
我们看一下样例：

4
1 1
0 2
2 0
2 2

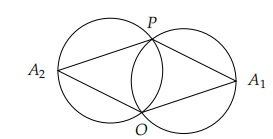
如图所示，我们选（0,2）为P,线段op对应的角中，∠PA₂O=∠OA₃P，说明A2，A3也在圆上，再加上p点，一共是三个，答案就是三

题解：

我一开始是暴力求解，直接枚举两个点，再枚举其他点看在不在边界上，复杂度是O(n³),但显然不行

思路1：

原点肯定在边界，我们可以先枚举一个点p，原点O与p组成线段op，op是圆上的一个弦，再枚举其他点A，根据“同弧所对的圆周角相等”，我们计算出∠OAP，然后找到最多数（众数）即可。但是度数相同不一定在同一个圆上（如图），会关于OP对称，我们只需规定A只能在OP下方，这样就确定位置，即OP（向量） * OA(向量) < 0
时间复杂度O（n²log n）

代码：

#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef __int128_t LLL;
#define N 2000 + 5int n, ans = 1, X[N], Y[N];struct Frac
{LL fz, fm;Frac() : Frac(0, 1){}Frac(LL fz, LL fm) : fz(fz), fm(fm) {}bool operator < (const Frac &rhs){return (LLL) fz * rhs.fm < (LLL) fm * rhs.fz;//判断谁的角大 }bool operator == (const Frac &rhs)//判断角是否相等 {return (LLL) fz * rhs.fm == (LLL) fm * rhs.fz;}
}A[N];int Cross(int lhs, int rhs)//判断是否平行 
{return X[lhs] * Y[rhs] - X[rhs] * Y[lhs];
}int Dis2(int lhs, int rhs)//两点的距离的平方和 
{int dx = X[lhs] - X[rhs], dy = Y[lhs] - Y[rhs];return dx * dx + dy * dy;
}int Sgn(int x)//用以调整x的正负 
{if (x > 0) return 1;if (x < 0) return -1;return 0;
}Frac GetCosAngle2(int i, int j)
{int a2 = Dis2(0, i);//求边 int b2 = Dis2(i, j);int c2 = Dis2(0, j);int sgn = Sgn(b2 + c2 - a2);return Frac(1LL * sgn * (b2 + c2 - a2) * (b2 + c2 - a2), 4LL * b2 * c2);//赋值 //余弦定理 cosA=(b2+c2-a2)/2bc 
}int main()
{scanf("%d", &n);for (int i = 1; i <= n; i ++)scanf("%d%d", X + i, Y + i);for (int i = 1; i <= n; i ++){int cnt = 0;for (int j = 1; j <= n; j ++)if (Cross(i, j) > 0)A[++ cnt] = GetCosAngle2(i, j);sort(A + 1, A + cnt + 1);for (int l = 1, r; l <= cnt; l = r){for (r = l; A[l] == A[r] && r <= cnt; r ++) ;ans = max(ans, r - l + 1);}}printf("%d\n", ans);return 0;
}

思路二

任意两个线段的中垂线的交点作圆心，圆肯定过两个线段的四个点，又因为必过原点，所以枚举每一个点，求它与原点所做线段的中垂线，然后求中垂线的所有交点，记录交点数
也就是求每个三角形的外心
特判中垂线都平行的情况
具体求外心的方法：
a(x1,y1) b(x2,y2) c(x3,y3)
外心o（x,y）
外心是垂直平分线的交点，也就是外心到各点距离相等
(x1-x) * (x1-x)-(y1-y) * (y1-y)=(x2-x) * (x2-x)+(y2-y) * (y2-y);
(x2-x) * (x2-x)+(y2-y) * (y2-y)=(x3-x) * (x3-x)+(y3-y) * (y3-y);
化简：
2*(x2-x1)x+2(y2-y1)y=x2²+y2²-x1²-y1²;
2*(x3-x2)x+2(y3-y2)y=x3²+y3²-x2²-y2²;
A1=2*(x2-x1)；
B1=2*(y2-y1)；
C1=x2²+y2²-x1²-y1²;
A2=2*(x3-x2)；
B2=2*(y3-y2)；
C2=x3²+y3²-x2²-y2²;
所以
A1x+B1y=C1;
A2x+B2y=C2;
结论：
x=((C1B2)-(C2B1))/((A1B2)-(A2B1))；
y=((A1C2)-(A2C1))/((A1B2)-(A2B1))；

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
const ll mod=998244353;
double eqs=1e-6;
struct Point{double x,y;Point(){}Point(double xx,double yy){x=xx;y=yy;}
}e[maxn];
Point operator+(Point a,Point b){  //向量加return Point(a.x+b.x,a.y+b.y);
}
Point operator-(Point a,Point b){ //向量减return Point(a.x-b.x,a.y-b.y);
}
double sqr(double x){return x*x;
}
double dis(Point a,Point b){ //求ab的长度return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));
}
Point Circum(Point a,Point b,Point c){ //三角形外心double x1=a.x,y1=a.y;double x2=b.x,y2=b.y;double x3=c.x,y3=c.y;double a1=2*(x2-x1);double b1=2*(y2-y1);double c1=x2*x2+y2*y2-x1*x1-y1*y1;// double a2=2*(x3-x2);double b2=2*(y3-y2);double c2=x3*x3+y3*y3-x2*x2-y2*y2;double x=(c1*b2-c2*b1)/(a1*b2-a2*b1);double y=(a1*c2-a2*c1)/(a1*b2-a2*b1);return Point(x,y);
}
map<pair<double,double>,int> m;
int main()
{int n;scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%lf %lf",&e[i].x,&e[i].y);}Point o=Point(0,0);int ans=0;for(int i=1;i<=n;i++){m.clear();for(int j=1;j<=n;j++){if(e[i].x*e[j].y-e[j].x*e[i].y<=eqs) continue;//如果平行 Point oo=Circum(o,e[i],e[j]);ans=max(++m[make_pair(oo.x,oo.y)],ans);}}printf("%d\n",ans+1);return 0;
}