正题

luogu 7599[APIO 2021 T2]

---

题目大意

给你一排树中每棵树的高度，每次跳跃可以跳到左/右边第一棵比该树高的树，问你从A-B中某棵树跳到C-D中的某棵树的最小步数（$A⩽B<C⩽D$）

---

解题思路

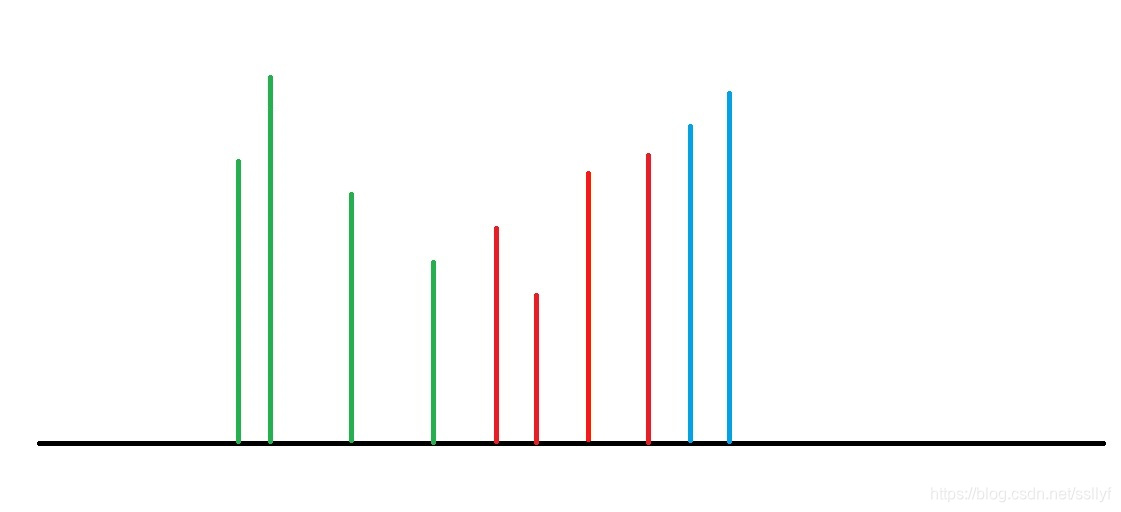
上图为例，绿色为起点，蓝色为终点

对于起点，不难发现，要选择低于最高终点的点中尽量高度，且右边的起点都比它低

低于最高终点保证了可以跳到终点，而最高的保证了跳的步数尽可能少，如果右边有比它高的，通过前面的性质，可以发现无法跳到终点（用倍增实现）

起点确定之后考虑往左右跳，由于$A⩽B<C⩽D$，往终点走一定是往右跳

那么往左有什么意义呢，对于4,2,3,4,5，当位于2时，往右跳到5要3步，而先往左跳一步只要两步，由此，往左跳的高度如果大于右边若干树的高度，那么往左跳可以使答案跟优

那么把跳跃分成往上和往右两步，设$f{j}_{i,j}$为位于i向上跳$2^j$步的最高高度，因为跳到右边可以使往右跳少一步，所以往上跳一定能使往右跳步数减少，且跳得越高，少得越多

所以往上跳跳到第一个点，使得该点高于起点终点之间的所有点，然后往右跳即可

---

代码

#include<cmath>
#include<vector>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define ll long long
#define NN 200021
using namespace std;
int n, m, v, x, A, B, C, D, lg, bg, hed, top, ans;
int h[NN], d[NN], lj[NN][20], rj[NN][20], hj[NN][20];
struct node
{int v, s;bool operator <(const node &b) const{return s > b.s;}
}b[NN];
struct Tree//线段树找最大
{int a[NN<<2];#define ls x*2#define rs x*2+1void build(int x, int l, int r){if (l == r){a[x] = h[l];return;}int mid = l + r >> 1;build(ls, l, mid);build(rs, mid + 1, r);a[x] = max(a[ls], a[rs]);return;}int ask(int x, int L, int R, int l, int r){if (L == l && R == r) return a[x];int mid = L + R >> 1;if (r <= mid) return ask(ls, L, mid, l, r);else if (l > mid) return ask(rs, mid + 1, R, l, r);else return max(ask(ls, L, mid, l, mid), ask(rs, mid + 1, R, mid + 1, r));}
}T;void init(int N, std::vector<int> H)
{n = N;int lg = log2(n);for (int i = 1; i <= n; ++i){h[i] = H[i - 1];b[i].v = i;b[i].s = h[i];lj[i][0] = i;for (int j = 1; j <= log2(i); ++j)//向左跳，找起点，存的是最高高度if (h[lj[i][j - 1]] > h[lj[i - (1<<(j - 1))][j - 1]]) lj[i][j] = lj[i][j - 1];else lj[i][j] = lj[i - (1<<(j - 1))][j - 1];}for (int i = 1; i <= n; ++i)//向高跳{while(h[d[top]] < h[i] && top) top--;hj[i][0] = d[top];d[++top] = i;}top = 0;for (int i = n; i > 0; --i){while(h[d[top]] < h[i] && top) top--;if (h[hj[i][0]] < h[d[top]]) hj[i][0] = d[top];rj[i][0] = d[top];for (int j = 1; j <= lg; ++j)//向右跳rj[i][j] = rj[rj[i][j - 1]][j - 1];d[++top] = i;}sort(b + 1, b + 1 + n);for (int i = 1; i <= n; ++i)for (int j = 1; j <= lg; ++j)hj[b[i].v][j] = hj[hj[b[i].v][j - 1]][j - 1];//倍增T.build(1, 1, n);
}int minimum_jumps(int A, int B, int C, int D)
{A++;B++;C++;D++;lg = log2(n);hed  = T.ask(1, 1, n, C, D);if (B + 1 <= C - 1) v = T.ask(1, 1, n, B + 1, C - 1);else{if (h[B] < hed) return 1;return -1;}if (v > hed) return -1;x = B;bg = B;for (int i = lg; i >= 0; --i)if (h[lj[x][i]] <= hed && x - (1<<i) + 1 >= A){if (h[bg] < h[lj[x][i]]) bg = lj[x][i];//找起点x -= (1<<i);}ans = 0;for (int i = lg; i >= 0; --i)if (hj[bg][i] && h[hj[bg][i]] < v){bg = hj[bg][i];//向高跳ans += (1<<i);}if (hj[bg][0] && h[hj[bg][0]] < hed && h[bg] < v){bg = hj[bg][0];ans++;}for (int i = lg; i >= 0; --i)if (rj[bg][i] && rj[bg][i] < C)//向右跳{bg = rj[bg][i];ans += (1<<i);}if (h[bg] <= hed) return ans + 1;else return -1;
}