引言

有一类题目:要求在区间上维护信息，比如带修改区间求和问题。考虑到枚举求和肯定会超时，我们可以通过一些数据结构来维护信息，例如线段树。
它功能强大，支持区间求和，区间求最值、区间修改等一系列操作。

思想

线段树，是一种二叉搜索树（即每个结点最多有两棵子树，通常叫做左右子树）。
它将一段区间划分为若干单位区间，每一个节点都储存着一段区间［L，R］的信息，其中叶子节点L＝R。它的大致思想是:将区间［1，n］平均分成2个小区间，再将小区间平均分成2个更小区间…以此类推，直到区间长度变为1无法分成两个更小的区间。通过对这些小区间进行修改、查询，来实现对大区间的修改、查询。
用线段树维护的问题必须满足可以用两个小区间的信息合并成大区间信息，否则是不可能将大问题划分成子问题来解决的。

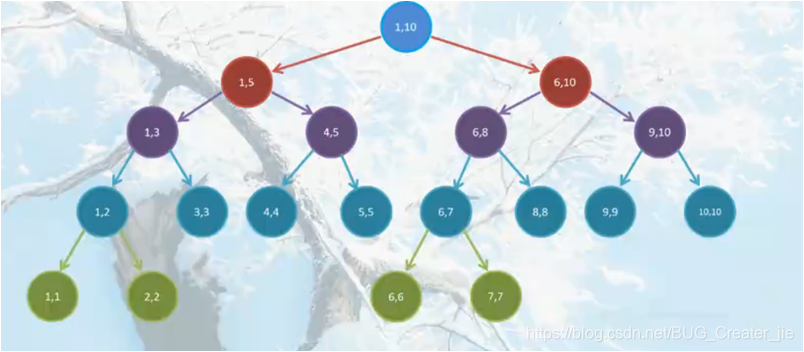
下图就是一棵［1，10］的线段树的分解过程。（相同颜色的节点在同一层）
可以证明，线段树的最大深度不超过log2n
在这里插入图片描述

模板

整体来说都是在贯彻递归二分分治的思想。注意k结点的两个孩子编号应分别为2k 和 2k+1
注意：关于线段树的数组要开到4n（最差时)！

建树

思想:常见的做法是遍历整棵线段树，设当前遍历到的节点所代表的区间为［l，r］，设中点mid＝（l＋r）/2，则左子树区间［l,mid］，右子树的区间为［mid＋1，r］，注意要递归到线段树的叶节点才结束，并给每一个节点赋值，叶子节点直接赋值，非叶子节点信息由左右子树信息合并而来。

void build(int k,int l,int r){if(l==r){sum[k]=f[l];return;}int mid=(l+r)>>1;build(2*k,l,mid);build(2*k+1,mid+1,r);sum[k]=sum[2*k]+sum[2*k+1];
}

单点修改 / 查询

~~用树状数组不好吗~~
思想:如果当前遍历到目标节点，就返回节点信息。如果不是，设查询位置为x，当前结点区间范围为了［l，r］，中点为mid，若x≤mid，则x在左子树的区间，递归当前结点的左孩子；否则x在右子树的区间，递归它的右孩子。

int dotquery(int k,int l,int r,int x){if(l==x)return sum[k];int mid=(l+r) /2;int res=0;if(x<=mid)	return dotquery(2*k,l,mid,x);else return dotquery(2*k+1,mid+1,r,x);
} void dotchange(int k,int l,int r,int x,int v){if(l==r){sum[k]+=v;return;}int mid=(l+r) /2;if(x<=mid) dotchange(2*k,l,mid,x,v);else dotchange(2*k+1,mid+1,r,x,v);sum[k]=sum[2*k]+sum[2*k+1];
}

区间修改/查询

区间查询:
设待查询区间为［x，y］，如果当前遍历到的区间被查询区间包含，就直接返回节点信息。如果不是，设当前结点区间范围为［l,r］中点为mid，如果x≤mid，则待查询区间与［l,mid]有交集，递归［l,mid］；如果y＞mid，则待查询区间与［mid＋1,r］有交集，递归［mid＋1,r］，最后将返回的信息合并就是区间［x,y］的答案。
区间修改：
延续区间查询的思想，我们可以找出所有信息发生改变的节点，可现在有一核心问题:我们并不能直接在这些节点上修改，若全部修改，复杂度难以承受。所以，区间修改的关键思路是:只修改对查询有用的点。为此，我们引入“懒标记＂的概念。
懒标记:若遍历到的节点带有懒标记，则立即修改当前节点的信息，并把标记下放到左右儿子，然而左右子树的信息不变动，只有遍历到左/右节点时才修改其信息

void Add(int k,int l,int r,int v){add[k]+=v;sum[k]+=(ll)(r-l+1)*v;return;
}
void pushdown(int k,int l,int r,int mid){if(add[k]==0) return;Add(2*k,l,mid,add[k]);Add(2*k+1,mid+1,r,add[k]);add[k]=0;
}
void longchange(int k,int l,int r,int x,int y,int v){if(x<=l&&r<=y){Add(k,l,r,v);return;}int mid=(l+r)>>1;pushdown(k,l,r,mid);if(x<=mid) longchange(2*k,l,mid,x,y,v);if(y>=mid+1) longchange(2*k+1,mid+1,r,x,y,v);sum[k]=sum[2*k]+sum[2*k+1];
}
ll longquery(int k,int l,int r,int x,int y){if(x<=l&&r<=y) return sum[k];int mid=(l+r)>>1;pushdown(k,l,r,mid);ll res=0;if(x<=mid) res+=longquery(2*k,l,mid,x,y);if(y>=mid+1) res+=longquery(2*k+1,mid+1,r,x,y);return res;
}